19 Out Of 30 Percentage
candidatos
Sep 22, 2025 · 5 min read
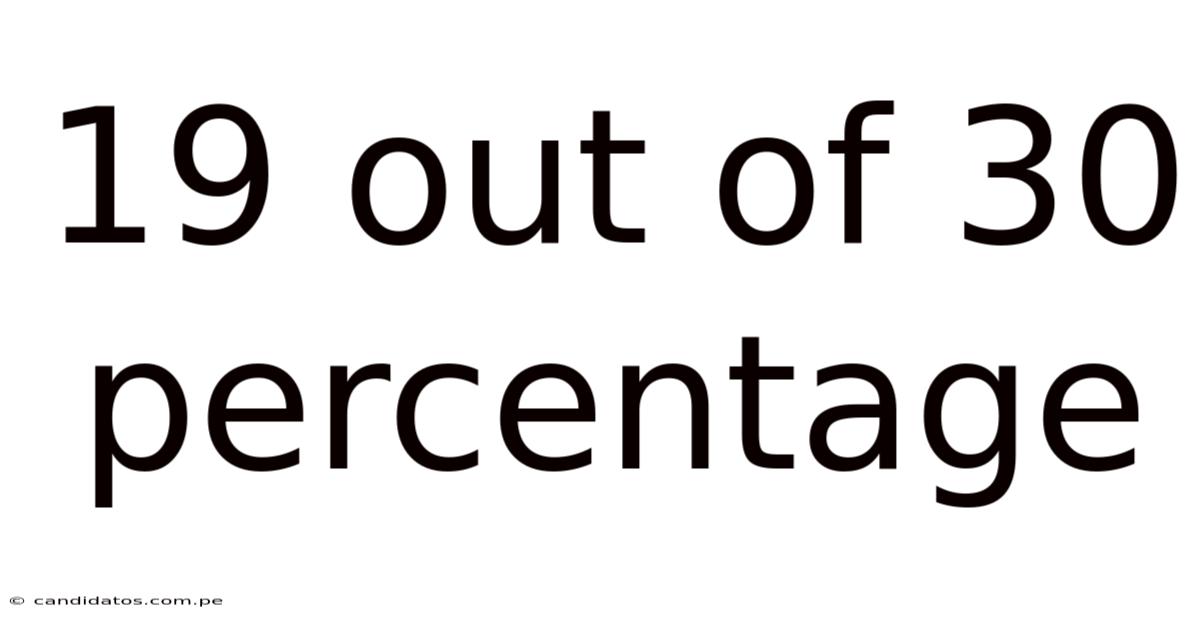
Table of Contents
Understanding 19 out of 30: Percentage Calculations and Real-World Applications
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from academic assessments to financial planning and beyond. This article delves into the intricacies of calculating percentages, specifically focusing on understanding what 19 out of 30 represents as a percentage, and exploring the broader implications of percentage calculations in everyday scenarios. We'll cover the calculation itself, explore different methods, discuss real-world applications, and address common misconceptions.
Calculating 19 out of 30 as a Percentage: A Step-by-Step Guide
The core concept behind percentage calculations is expressing a part of a whole as a fraction of 100. To calculate 19 out of 30 as a percentage, we follow these steps:
-
Formulate the Fraction: Represent the problem as a fraction. In this case, 19 (the part) is out of 30 (the whole), giving us the fraction 19/30.
-
Convert the Fraction to a Decimal: To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number). 19 divided by 30 equals approximately 0.6333.
-
Convert the Decimal to a Percentage: Multiply the decimal by 100. 0.6333 multiplied by 100 equals 63.33%.
Therefore, 19 out of 30 is approximately 63.33%.
Alternative Calculation Methods
While the above method is straightforward, there are alternative approaches, particularly useful depending on the tools available:
-
Using a Calculator: Most calculators have a percentage function. Simply enter 19 ÷ 30 and then press the % button. The calculator will automatically display the result as a percentage.
-
Using Spreadsheet Software: Spreadsheet programs like Microsoft Excel or Google Sheets offer built-in functions for percentage calculations. The formula
=19/30*100will directly output the percentage. -
Mental Estimation: For quick estimations, you can round the numbers. Thinking of 19 as approximately 20 out of 30 gives you roughly 2/3, which is approximately 66.67%. This provides a good ballpark figure.
Real-World Applications: Understanding Percentages in Context
The ability to calculate percentages has widespread applications in diverse fields:
-
Academic Performance: A student scoring 19 out of 30 on a test would have achieved a grade of approximately 63.33%. This allows for easy comparison of performance across different assessments, even if they have varying total marks.
-
Financial Calculations: Percentages are crucial for understanding interest rates, discounts, taxes, and investment returns. For instance, a 10% discount on a $100 item means a saving of $10.
-
Statistical Analysis: Percentages are commonly used to represent proportions and probabilities in various statistical analyses. For example, if 19 out of 30 people surveyed prefer a particular product, this represents a 63.33% preference rate.
-
Data Representation: Percentages are an effective way to visualize data and communicate findings. Graphs and charts frequently use percentages to illustrate proportions within datasets. Understanding these percentages allows for better comprehension of data trends and patterns.
-
Business and Economics: In business, percentages are essential for tracking sales figures, profit margins, market share, and growth rates. Analyzing percentage changes helps to identify trends and make informed decisions.
-
Healthcare: Percentages are vital in numerous healthcare contexts, for instance representing the success rate of a medical treatment or the prevalence of a specific disease in a population.
-
Sports Statistics: In sports, percentages are often used to represent batting averages, shooting percentages, and win/loss records. These statistics help to compare the performance of players and teams.
Misconceptions about Percentages: Avoiding Common Errors
Several common misconceptions surround percentage calculations:
-
Confusion with Fractions and Decimals: Remembering the interconversion between fractions, decimals, and percentages is vital. A percentage is simply a fraction expressed out of 100.
-
Adding Percentages Incorrectly: Percentages cannot always be added directly. For instance, a 10% increase followed by a 10% decrease does not result in a net change of 0%. The second 10% decrease is applied to a new base value (after the initial increase), leading to a slightly lower final value.
-
Incorrect Interpretation of Percentage Change: Understanding whether a percentage represents a change from an initial value or a proportion of a whole is important. A statement like "sales increased by 20%" indicates a percentage change, whereas "20% of sales were from online channels" indicates a proportion.
-
Ignoring the Base Value: The base value (the 'whole' or the 'original amount') is essential when working with percentages. Without knowing the base, the percentage is meaningless. For example, stating that a value increased by 10% is incomplete without specifying the original value.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage increase or decrease?
- A: To calculate a percentage increase, find the difference between the new and original values, divide this difference by the original value, and then multiply by 100. A percentage decrease follows the same process.
-
Q: What if I have a percentage and need to find the original value?
- A: This involves working backward. If you know the final value and the percentage increase/decrease, you can use algebraic equations to determine the original value.
-
Q: How can I improve my understanding of percentages?
- A: Practice regularly by working through various problems. Utilize online resources, educational materials, and real-world examples to reinforce your understanding.
Conclusion: Mastering Percentage Calculations for a Brighter Future
Mastering percentage calculations is more than just memorizing formulas; it's about gaining a deeper understanding of numerical relationships and their application in daily life. From assessing academic performance to making informed financial decisions and interpreting statistical data, the ability to work confidently with percentages equips you with a powerful skillset applicable across various domains. By understanding the underlying principles, practicing different calculation methods, and being aware of common misconceptions, you can build a strong foundation for tackling percentage-related problems effectively and confidently. The journey to mastery is a continuous process of learning and application – so keep practicing, and you'll find yourself increasingly adept at navigating the world of percentages. Remember that 19 out of 30, approximately 63.33%, is just one example; the principles applied here can be generalized to any percentage calculation.
Latest Posts
Latest Posts
-
Life Cycle Of The Tree
Sep 22, 2025
-
Best Names For A Duck
Sep 22, 2025
-
Decimals From Smallest To Largest
Sep 22, 2025
-
16 X 3 X 2
Sep 22, 2025
-
18 24 As A Percent
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 19 Out Of 30 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.