18 24 As A Percent
candidatos
Sep 22, 2025 · 6 min read
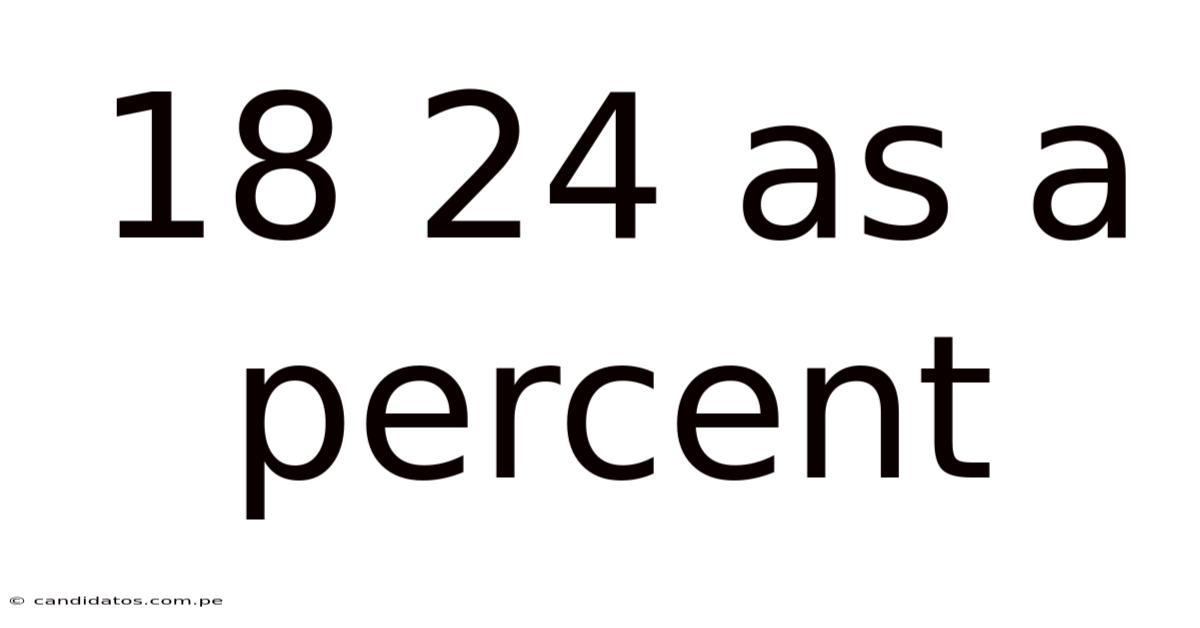
Table of Contents
18 out of 24 as a Percent: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various fields, from everyday budgeting and shopping to complex scientific research and financial analysis. Understanding how to express a part of a whole as a percentage is crucial for interpreting data, making informed decisions, and communicating effectively. This article will guide you through calculating "18 out of 24 as a percent," explaining the process step-by-step and delving into the underlying mathematical principles. We'll also explore related concepts and answer frequently asked questions, equipping you with a comprehensive understanding of percentage calculations.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are a convenient way to compare proportions and express ratios, making them indispensable in numerous contexts.
Calculating 18 out of 24 as a Percentage: A Step-by-Step Guide
To determine what percentage 18 represents out of 24, we follow these simple steps:
Step 1: Set up the Fraction
First, represent the given numbers as a fraction. The part (18) becomes the numerator, and the whole (24) becomes the denominator:
18/24
Step 2: Convert the Fraction to a Decimal
Divide the numerator (18) by the denominator (24):
18 ÷ 24 = 0.75
Step 3: Convert the Decimal to a Percentage
Multiply the decimal by 100 and add the percentage sign (%):
0.75 x 100 = 75%
Therefore, 18 out of 24 is 75%.
Different Approaches to the Calculation
While the method above is the most straightforward, there are other ways to arrive at the same result. Let's explore a couple of alternative approaches:
Method 2: Simplifying the Fraction First
Before converting to a decimal, you can simplify the fraction 18/24 by finding the greatest common divisor (GCD) of both numbers. The GCD of 18 and 24 is 6. Dividing both the numerator and denominator by 6 gives:
18 ÷ 6 / 24 ÷ 6 = 3/4
Now, convert the simplified fraction 3/4 to a decimal:
3 ÷ 4 = 0.75
Finally, convert the decimal to a percentage:
0.75 x 100 = 75%
This method simplifies the calculation, particularly when dealing with larger numbers.
Method 3: Using Proportions
You can also solve this using proportions. We can set up a proportion where x represents the percentage we want to find:
18/24 = x/100
To solve for x, cross-multiply:
24x = 1800
Divide both sides by 24:
x = 1800 ÷ 24 = 75
Therefore, x = 75%, confirming our previous result.
Understanding the Concept of Ratios and Proportions
The calculation of percentages is intrinsically linked to the concepts of ratios and proportions. A ratio is a comparison of two quantities, often expressed as a fraction. In our example, the ratio of 18 to 24 (18:24) represents the relationship between the part and the whole. A proportion is a statement that two ratios are equal. We used a proportion in Method 3 to solve for the unknown percentage. Understanding these fundamental mathematical concepts is crucial for mastering percentage calculations.
Applications of Percentage Calculations in Real Life
Percentage calculations are ubiquitous in everyday life. Here are just a few examples:
- Shopping: Calculating discounts, sales tax, and tips. For example, a 20% discount on a $100 item means a saving of $20.
- Finance: Determining interest rates, loan repayments, and investment returns. Understanding compound interest involves repeated percentage calculations.
- Education: Calculating grades, test scores, and overall performance. A student scoring 80% on an exam implies a correct answer rate of 80 out of 100.
- Science: Expressing experimental results, statistical data, and error margins. Scientific papers often present data as percentages to facilitate comparison and interpretation.
- Data Analysis: Presenting data visually using charts and graphs that incorporate percentages. Pie charts are a common example, where each segment represents a percentage of the total.
Advanced Percentage Calculations: Finding the Whole or the Part
While calculating a percentage from a part and a whole is common, you might encounter situations where you need to find either the whole or the part, given the percentage and either the part or the whole, respectively. Let's examine these scenarios:
Scenario 1: Finding the Whole
-
Problem: 75% of a number is 18. What is the number?
-
Solution: Let the number be 'x'. We can set up the equation:
0.75x = 18
Divide both sides by 0.75:
x = 18 ÷ 0.75 = 24
Therefore, the number is 24.
Scenario 2: Finding the Part
-
Problem: What is 25% of 24?
-
Solution: Multiply 24 by 0.25:
24 x 0.25 = 6
Therefore, 25% of 24 is 6.
Frequently Asked Questions (FAQs)
Q1: What is the difference between a percentage and a proportion?
A percentage is a specific type of proportion expressed as a fraction of 100. A proportion is a more general term that compares two quantities. All percentages are proportions, but not all proportions are percentages.
Q2: How can I convert a fraction to a percentage quickly?
Divide the numerator by the denominator and multiply the result by 100. Alternatively, if you can simplify the fraction to a denominator of 100, the numerator directly represents the percentage.
Q3: Why are percentages so widely used?
Percentages offer a standardized and easily understandable way to compare ratios and proportions across different contexts. They simplify complex relationships and make data more accessible.
Q4: Are there any online calculators for percentage calculations?
Yes, many websites and apps offer online percentage calculators that can automate the process, particularly useful for more complex calculations. However, understanding the underlying principles is still valuable.
Q5: What are some common errors to avoid when calculating percentages?
- Incorrect order of operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS).
- Incorrect decimal placement: Be mindful of decimal points when converting between decimals and percentages.
- Confusion between part and whole: Clearly identify the part and the whole in the problem.
Conclusion
Calculating percentages is a fundamental skill with wide-ranging applications. Understanding the principles behind percentage calculations, from basic conversions to more advanced applications, empowers you to interpret data, make informed decisions, and communicate effectively in various aspects of life. Mastering these concepts allows you to confidently tackle percentage-related problems and confidently analyze quantitative information presented in percentages. Remember the three steps: fraction, decimal, percentage, and you'll always reach the right answer. By practicing different methods and understanding the underlying mathematical concepts, you can build a strong foundation in percentage calculations and apply this knowledge effectively in your personal and professional life.
Latest Posts
Latest Posts
-
Distance Between Sun And Neptune
Sep 22, 2025
-
5 Letter Word Starts Pi
Sep 22, 2025
-
Converting Units Of Measurement Worksheets
Sep 22, 2025
-
1 X 2 Y 2
Sep 22, 2025
-
5 Letter Words Ending Ie
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 18 24 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.