16 X 3 X 2
candidatos
Sep 22, 2025 · 6 min read
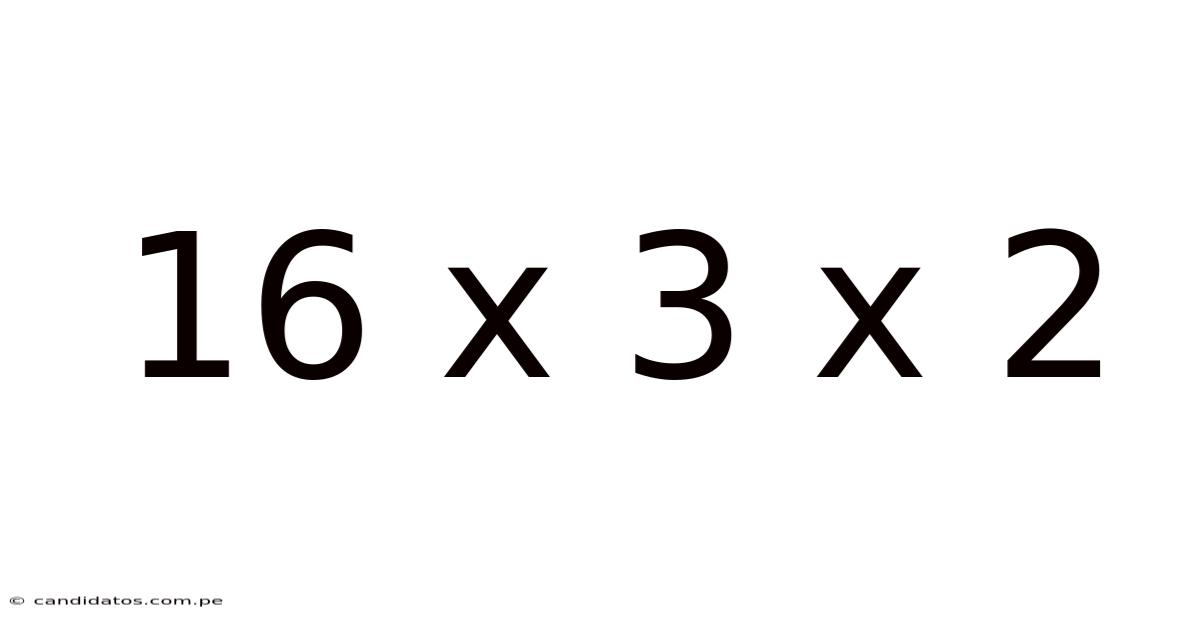
Table of Contents
Unveiling the Mystery of 16 x 3 x 2: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 16 x 3 x 2, delving far beyond the basic arithmetic to uncover the underlying mathematical principles and its diverse applications in various fields. We'll move beyond simply arriving at the answer, investigating the properties of multiplication, different calculation methods, and the relevance of this seemingly simple equation in more complex mathematical concepts and real-world scenarios. Understanding this seemingly simple equation lays a foundation for understanding more complex mathematical concepts.
Understanding the Fundamentals: Multiplication
Before we tackle 16 x 3 x 2, let's establish a solid understanding of multiplication. Multiplication is a fundamental arithmetic operation representing repeated addition. For instance, 3 x 2 means adding 2 three times (2 + 2 + 2 = 6). It's a crucial operation for many aspects of mathematics and beyond. The numbers involved in multiplication have specific names: the numbers being multiplied are called factors or multiplicands, and the result is the product.
In our example, 16, 3, and 2 are the factors, and their product is what we aim to calculate. Understanding the commutative, associative, and distributive properties of multiplication is key to efficiently solving this and more complex problems.
-
Commutative Property: The order of the factors doesn't change the product. This means 16 x 3 x 2 is the same as 3 x 16 x 2, 2 x 16 x 3, and so on.
-
Associative Property: The way we group the factors doesn't affect the product. We can calculate (16 x 3) x 2 or 16 x (3 x 2) and get the same result.
-
Distributive Property: This property links multiplication and addition. It states that a(b + c) = ab + ac. While not directly applicable to our problem in its simplest form, understanding this property is vital for solving more intricate equations involving both multiplication and addition.
Calculating 16 x 3 x 2: Different Approaches
Now let's calculate 16 x 3 x 2 using different methods, highlighting the advantages of each:
Method 1: Sequential Multiplication
The most straightforward approach is to multiply the numbers sequentially:
- 16 x 3 = 48
- 48 x 2 = 96
Therefore, 16 x 3 x 2 = 96.
Method 2: Utilizing the Associative Property
Using the associative property, we can rearrange the calculation for easier mental math:
- 3 x 2 = 6
- 16 x 6 = 96
This approach simplifies the calculation by initially working with smaller, easier-to-manage numbers. This is particularly useful for mental calculations.
Method 3: Breaking Down Numbers
We can also break down the numbers into simpler factors to make the calculation easier. For example:
- 16 can be written as 8 x 2
- So, the equation becomes (8 x 2) x 3 x 2
- This can be rearranged as 8 x (2 x 3 x 2) = 8 x 12 = 96
The Significance of 96: Exploring its Mathematical Context
The product of 16 x 3 x 2, which is 96, is not just a random number; it holds significance within several mathematical contexts:
-
Factors and Multiples: 96 has numerous factors, including 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96. Understanding factors is crucial in simplifying fractions and solving algebraic equations. It's also a multiple of many numbers, including 2, 3, 4, 6, 8, 12, 16, 24, 32, and 48.
-
Prime Factorization: Breaking down a number into its prime factors (factors that are only divisible by 1 and themselves) is a fundamental concept in number theory. The prime factorization of 96 is 2<sup>5</sup> x 3. This representation is unique to each number and is essential in various mathematical applications, particularly in cryptography.
-
Number Systems: 96 can be represented in different number systems. For instance, in binary (base-2), it's 1100000, and in hexadecimal (base-16), it's 60. This understanding is vital in computer science and digital systems.
Real-World Applications: Where 16 x 3 x 2 Might Appear
While seemingly simple, the concept of multiplication and the result 96 finds applications in various real-world scenarios:
-
Measurement and Geometry: Imagine calculating the volume of a rectangular prism (box). If the dimensions are 16 cm, 3 cm, and 2 cm, the volume would be 16 x 3 x 2 = 96 cubic centimeters. This applies to various fields from packaging design to construction.
-
Finance and Business: Calculating the total cost of 16 items priced at $3 each, bought in 2 sets, leads to 16 x 3 x 2 = $96. This concept extends to inventory management, sales calculations, and profit/loss analyses.
-
Data Analysis and Statistics: In data analysis, you might encounter scenarios where you need to multiply different data points. For example, calculating the total number of items across different categories, locations, or time periods might involve similar multiplications.
-
Everyday Calculations: Even simple daily tasks involve multiplication. For example, calculating the total number of cookies in 16 bags with 3 rows and 2 columns of cookies each.
Beyond the Basics: Expanding on the Concept
The seemingly basic calculation 16 x 3 x 2 opens doors to more complex mathematical concepts:
-
Algebra: Instead of fixed numbers, we can use variables (like x, y, z) to represent unknown quantities. This introduces algebraic equations where the concept of multiplication remains crucial for solving for unknown variables. For example, if we have an equation like 16xz = 96 and we know z = 2, we can easily solve for x.
-
Calculus: Calculus, the study of change, uses concepts of limits, derivatives, and integrals, and these all build upon a solid foundation in arithmetic, including multiplication.
-
Linear Algebra: Linear algebra deals with vectors and matrices, and multiplication plays a significant role in vector multiplication, matrix multiplication, and solving systems of linear equations.
-
Higher-Level Mathematics: The principles underlying this simple multiplication are fundamental to more advanced mathematical fields like number theory, abstract algebra, and topology.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate 16 x 3 x 2?
A: The easiest way depends on your preference and mathematical skills. Multiplying 3 x 2 first (giving 6) and then multiplying by 16 often simplifies the calculation.
Q: What are some real-world examples where this calculation might be used?
A: Real-world examples are numerous. Calculating the volume of a rectangular box, the total cost of multiple items, or the number of items in a grid arrangement are just a few.
Q: Why is understanding the properties of multiplication important?
A: Understanding the commutative, associative, and distributive properties allows for more efficient and flexible calculations, especially with more complex equations. It's crucial for problem-solving and applying mathematics to real-world situations.
Q: Is there a way to calculate this without using a calculator or pen and paper?
A: Yes, utilizing mental math strategies such as the associative property and breaking down numbers into smaller, more manageable factors can allow you to calculate 16 x 3 x 2 mentally.
Conclusion
The seemingly trivial calculation of 16 x 3 x 2 serves as a gateway to a deeper understanding of multiplication, its properties, and its extensive applications across various disciplines. While the answer is simply 96, the journey to obtain it and the exploration of its mathematical context reveal the foundational role of this seemingly simple arithmetic operation in more complex mathematical concepts and real-world scenarios. Mastering this foundational understanding paves the way for success in more advanced mathematical pursuits. The seemingly simple equation highlights that even the most basic elements of mathematics hold significant importance and potential for application across various areas of life.
Latest Posts
Latest Posts
-
Bill Of Rights Act 1990
Sep 22, 2025
-
Words That Rhyme With Nice
Sep 22, 2025
-
Distance Between Sun And Neptune
Sep 22, 2025
-
5 Letter Word Starts Pi
Sep 22, 2025
-
Converting Units Of Measurement Worksheets
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 16 X 3 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.