X 2 Y 2 1
candidatos
Sep 19, 2025 · 7 min read
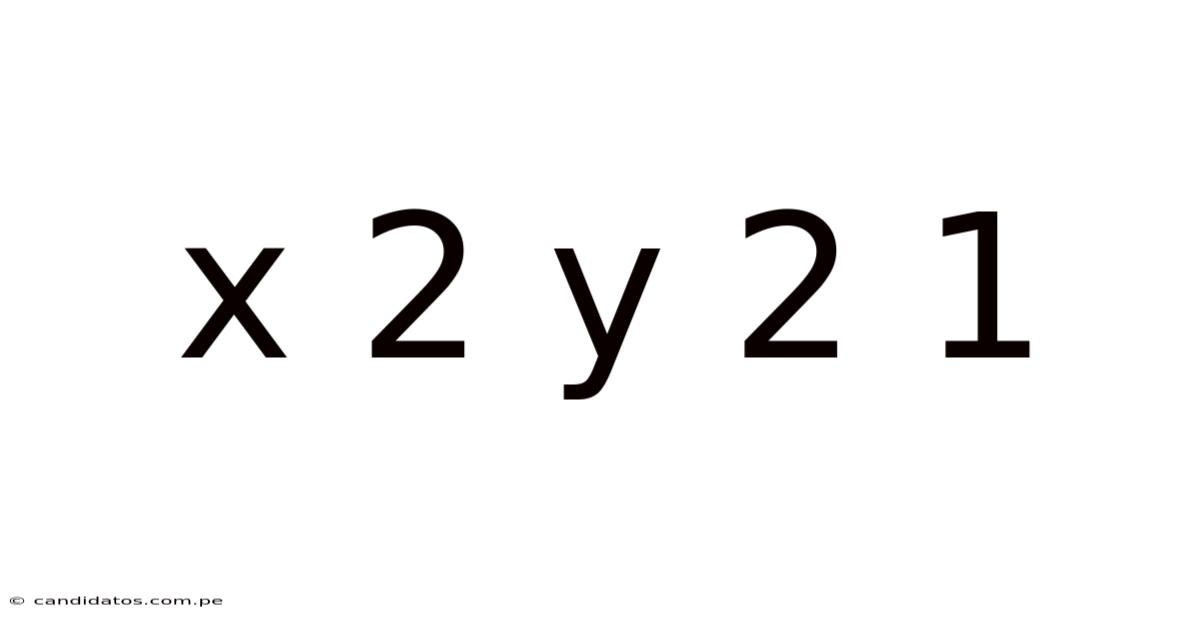
Table of Contents
Decoding the Mathematical Mystery: x² + y² = 1
The equation x² + y² = 1 might seem simple at first glance, but it holds a wealth of mathematical significance and represents a cornerstone concept in various fields. This seemingly straightforward equation describes the unit circle, a fundamental shape in geometry and trigonometry, with far-reaching applications in calculus, physics, and even computer graphics. This article delves deep into the equation x² + y² = 1, exploring its geometrical representation, algebraic properties, and practical applications.
Introduction: The Unit Circle and its Significance
At its core, x² + y² = 1 defines a circle centered at the origin (0,0) with a radius of 1. This is why it's called the unit circle. Its simplicity belies its importance. The unit circle provides a visual and algebraic framework for understanding trigonometric functions, particularly sine and cosine. Any point (x, y) on the unit circle can be defined using the angle θ (theta) formed by the positive x-axis and the line segment connecting the origin to that point. This connection forms the basis of many trigonometric identities and calculations. Understanding the unit circle is essential for anyone pursuing further studies in mathematics, physics, engineering, or computer science.
Understanding the Geometry: Points, Radius, and Angles
The equation itself is derived directly from the Pythagorean theorem. Consider a right-angled triangle formed by a point (x, y) on the circle, the x-axis, and a line segment connecting the point to the origin. The legs of this triangle have lengths x and y, and the hypotenuse is the distance from the origin to the point (x,y), which is the radius of the circle. Since the radius of the unit circle is 1, the Pythagorean theorem (a² + b² = c²) becomes x² + y² = 1². This elegantly demonstrates the inherent geometric relationship embedded within the equation.
- Points on the Circle: Any pair of (x, y) coordinates satisfying the equation x² + y² = 1 represents a point lying precisely on the circumference of the unit circle.
- Radius: The radius of the circle is implicitly defined as 1, as it's the distance from the origin (0,0) to any point (x, y) satisfying the equation.
- Angles (θ): The angle θ formed between the positive x-axis and the line segment connecting the origin to a point (x, y) on the circle is crucial for understanding the trigonometric relationships.
Trigonometric Relationships: Sine, Cosine, and Tangent
The power of the unit circle becomes truly apparent when we connect it to trigonometry. For any point (x, y) on the unit circle corresponding to an angle θ:
- x = cos(θ): The x-coordinate is equal to the cosine of the angle θ.
- y = sin(θ): The y-coordinate is equal to the sine of the angle θ.
- y/x = tan(θ): The tangent of the angle θ is the ratio of the y-coordinate to the x-coordinate (provided x ≠ 0).
This direct relationship between the coordinates of a point on the unit circle and trigonometric functions is incredibly useful. It allows us to visualize trigonometric functions and derive various identities. For instance, the fundamental trigonometric identity sin²(θ) + cos²(θ) = 1 directly follows from the equation x² + y² = 1, highlighting the inherent connection between geometry and trigonometry.
Algebraic Manipulation and Solving Equations
The equation x² + y² = 1 can be manipulated algebraically to solve for one variable in terms of the other. For example, we can solve for y:
y = ±√(1 - x²)
This equation reveals that for any given x-coordinate within the range [-1, 1], there are two corresponding y-coordinates, reflecting the circle's symmetry about the x-axis. Similarly, we can solve for x:
x = ±√(1 - y²)
This shows the symmetry about the y-axis. These algebraic manipulations are vital for solving problems involving the unit circle and applying it in various contexts.
Applications in Calculus: Parametric Equations and Derivatives
In calculus, the unit circle is often represented using parametric equations. This means we express both x and y as functions of a parameter, typically the angle θ:
- x = cos(θ)
- y = sin(θ)
This parametric representation simplifies calculations involving derivatives and integrals. For example, finding the slope of the tangent line to the unit circle at a given point becomes straightforward using these parametric equations and calculating dy/dx.
Applications in Physics: Circular Motion and Oscillations
The unit circle is fundamentally important in physics, particularly in understanding circular motion and oscillatory systems. The x and y coordinates, representing cos(θ) and sin(θ) respectively, can describe the position of an object undergoing uniform circular motion. The angle θ represents the phase of the oscillation, while the radius represents the amplitude. This framework extends to analyzing simple harmonic motion (SHM) and other periodic phenomena.
Applications in Computer Graphics: 2D Transformations and Animations
In computer graphics, the unit circle plays a vital role in 2D transformations. Rotation transformations, for example, are often implemented using trigonometric functions derived from the unit circle. Animating circular motion or creating circular shapes in a computer graphics program relies heavily on the principles embedded within x² + y² = 1. Understanding the unit circle allows for efficient and accurate manipulation of graphical elements.
Beyond the Basics: Complex Numbers and the Complex Plane
The equation x² + y² = 1 extends its reach into the realm of complex numbers. In the complex plane, where the horizontal axis represents the real part and the vertical axis represents the imaginary part, the equation represents the set of all complex numbers with magnitude (or modulus) equal to 1. These numbers are often expressed in polar form as e^(iθ), where e is Euler's number and i is the imaginary unit. This connection links the unit circle to Euler's formula, one of the most elegant and significant equations in mathematics.
Frequently Asked Questions (FAQ)
Q: What happens if the radius isn't 1?
A: If the radius is 'r', the equation becomes x² + y² = r². This represents a circle with radius 'r' centered at the origin. The trigonometric relationships still apply, but the x and y coordinates will be scaled by the factor 'r'.
Q: Can the equation x² + y² = 1 represent anything other than a circle?
A: In the context of real numbers, x² + y² = 1 exclusively represents a circle. However, if we consider complex numbers, as mentioned earlier, it represents the set of complex numbers with a magnitude of 1.
Q: How can I graph x² + y² = 1?
A: The simplest way is to use graphing software or a graphing calculator. You can also manually plot points by selecting values for x (within the range [-1, 1]) and calculating the corresponding y values using y = ±√(1 - x²), and then plotting those (x, y) coordinates on a Cartesian plane.
Q: What are some real-world examples of the unit circle?
A: The rotating blades of a fan, the path of a satellite orbiting a planet (approximated as a circle), the circular motion of a Ferris wheel, and even the ripples created when you drop a pebble into calm water can all be modeled, at least partially, using the principles of the unit circle.
Conclusion: A Simple Equation with Profound Implications
The seemingly simple equation x² + y² = 1, representing the unit circle, forms a foundation for numerous mathematical concepts and applications across various scientific and technological fields. From understanding trigonometric functions and solving geometric problems to analyzing circular motion, modeling oscillations, and creating computer graphics, this equation proves to be remarkably versatile and powerful. Its elegance lies not just in its simplicity but in its ability to bridge seemingly disparate areas of mathematics and science, emphasizing the interconnectedness of mathematical concepts and their profound influence on our understanding of the world around us. Mastering the unit circle is not just about understanding a single equation; it's about gaining a deeper appreciation for the fundamental principles that underpin many areas of mathematics and its applications.
Latest Posts
Latest Posts
-
Start With Letter I Animals
Sep 20, 2025
-
Respect Crossword Clue 6 Letters
Sep 20, 2025
-
A Fist Within 4 Walls
Sep 20, 2025
-
3 12 As A Percent
Sep 20, 2025
-
3 5 Divided By 2
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.