3 5 Divided By 2
candidatos
Sep 20, 2025 · 6 min read
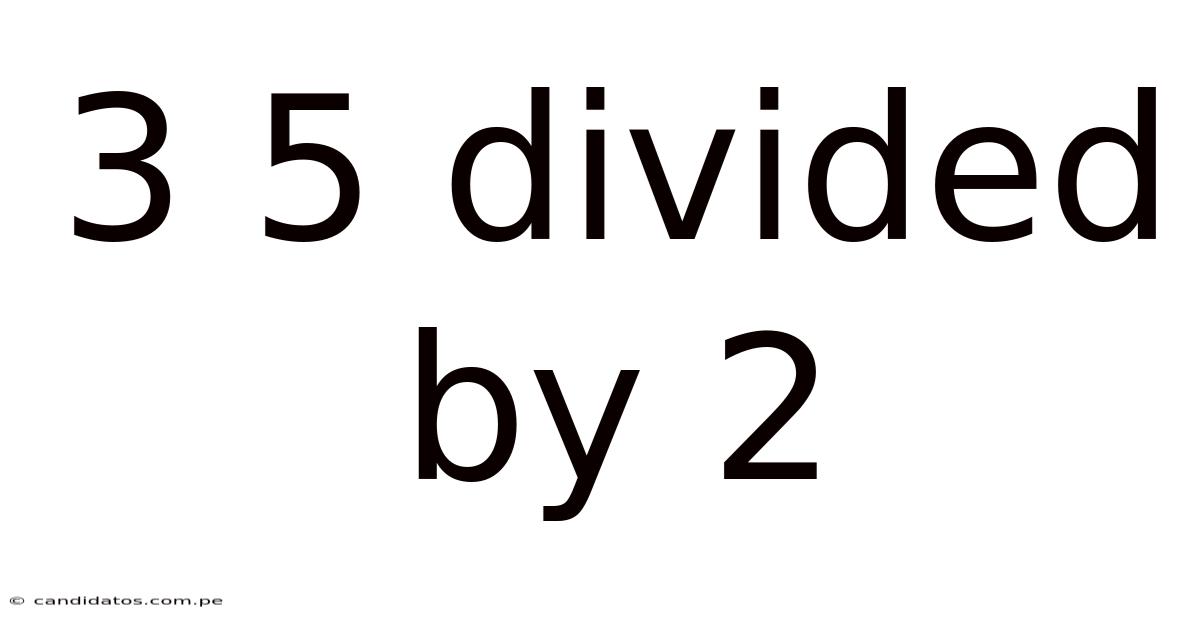
Table of Contents
Decoding 3.5 Divided by 2: A Deep Dive into Division with Decimals
Understanding division, especially when it involves decimals, is a cornerstone of mathematical literacy. This comprehensive guide will explore the seemingly simple calculation of 3.5 divided by 2, breaking it down step-by-step to reveal the underlying principles and applications. We'll move beyond just the answer to explore various methods, address common misconceptions, and delve into the broader implications of decimal division. This will equip you with a solid understanding not just of this specific problem, but of decimal division in general.
Introduction: Why This Matters
At first glance, 3.5 divided by 2 might seem trivial. However, mastering this seemingly basic operation is crucial for more complex mathematical concepts. It forms the foundation for understanding ratios, proportions, averages, and even more advanced topics in algebra, calculus, and beyond. Understanding how to handle decimals in division is particularly important in everyday life, from splitting bills fairly to calculating unit prices and converting measurements. This article will provide a thorough explanation, making the process clear and accessible to everyone, regardless of their mathematical background.
Method 1: Long Division
The traditional method for solving 3.5 divided by 2 is long division. This method reinforces fundamental mathematical understanding.
-
Set up the problem: Write the problem as a long division problem: 2 | 3.5
-
Divide the whole number: Divide 3 by 2. 2 goes into 3 one time (1). Write the 1 above the 3.
-
Subtract and bring down: Multiply 1 (your quotient) by 2 (your divisor), which is 2. Subtract 2 from 3, leaving 1. Bring down the 5 from the decimal portion of the dividend. You now have 15.
-
Divide the decimal part: Divide 15 by 2. 2 goes into 15 seven times (7). Write the 7 above the 5.
-
Subtract and finalize: Multiply 7 by 2, which is 14. Subtract 14 from 15, leaving 1. Since we're working with decimals, we can add a zero and continue the process to achieve a more precise answer, or we can express the remainder as a fraction (1/2) or a decimal (0.5).
Therefore, 3.5 divided by 2 = 1.75. Alternatively, we could express the answer as 1 and 3/4, which is mathematically equivalent.
Method 2: Fraction Conversion
Another way to approach this problem is by converting the decimal to a fraction. This method often simplifies the division process, especially for those who find fractions easier to work with than decimals.
-
Convert the decimal to a fraction: 3.5 can be written as the improper fraction 7/2 (since 3.5 = 3 + 1/2 = 6/2 + 1/2 = 7/2).
-
Divide the fractions: Dividing by 2 is the same as multiplying by its reciprocal, which is 1/2. So we have: (7/2) * (1/2) = 7/4
-
Convert back to decimal (if needed): To convert 7/4 back to a decimal, we divide 7 by 4. 4 goes into 7 once with a remainder of 3. We add a decimal point and a zero, bringing down the zero to make 30. 4 goes into 30 seven times with a remainder of 2. Adding another zero and continuing this process gives 1.75.
This method demonstrates the equivalence between fractions and decimals and reinforces the concept of reciprocal operations.
Method 3: Halving
A simpler approach for this specific problem leverages the fact that dividing by 2 is equivalent to halving.
-
Halve the whole number: Half of 3 is 1.5.
-
Halve the decimal part: Half of 0.5 is 0.25.
-
Combine the halves: Adding 1.5 and 0.25 gives 1.75.
This method is particularly intuitive and helpful for quickly solving similar problems involving dividing by 2. It demonstrates the practicality of applying conceptual understanding to simplify calculations.
The Scientific Explanation: Understanding the Underlying Principles
The division operation, at its core, represents the process of splitting a quantity into equal parts. When we divide 3.5 by 2, we're essentially asking: "If we have 3.5 units and we want to divide them into 2 equal groups, how many units will be in each group?"
The decimal portion of the dividend (3.5) requires careful attention. The decimal point represents a division by a power of 10. In 3.5, the '.5' represents 5/10 or 1/2. The division process extends this fractional representation, ensuring that each part of the dividend is equally divided amongst the specified number of groups. The result reflects the equal distribution of the whole number and the fractional part.
Practical Applications: Real-World Scenarios
Understanding decimal division isn't confined to the classroom; it's vital in numerous real-world scenarios:
- Sharing Costs: Splitting a restaurant bill equally among friends.
- Unit Pricing: Determining the price per item when buying in bulk.
- Measurement Conversions: Converting between metric and imperial units (e.g., kilometers to miles).
- Recipe Scaling: Adjusting recipe quantities to serve more or fewer people.
- Financial Calculations: Calculating interest rates, discounts, and profits.
- Scientific Calculations: Many scientific formulas involve decimal division.
These applications highlight the practical importance of mastering decimal division, making it a transferable skill applicable across various fields.
Frequently Asked Questions (FAQ)
-
What if I get a remainder? When working with decimals, you can add zeros after the decimal point and continue the division process to achieve a more precise answer. Alternatively, you can express the remainder as a fraction.
-
Can I use a calculator? Yes, calculators provide a quick and efficient way to solve decimal division problems. However, understanding the underlying principles remains crucial for comprehending the mathematical operations involved.
-
What if I'm dividing by a decimal? Dividing by a decimal involves a slightly different approach. You'll typically need to manipulate the divisor to become a whole number by multiplying both the divisor and the dividend by the same power of 10.
-
How can I improve my division skills? Practice regularly using various methods (long division, fraction conversion, estimation) to build confidence and accuracy. Start with simpler problems and gradually progress to more complex ones.
Conclusion: Beyond the Answer
This exploration of 3.5 divided by 2 goes far beyond simply obtaining the answer (1.75). It's about understanding the fundamental principles of division, the application of different methods, and the broader context of decimal operations. Mastering these concepts is essential not only for academic success but also for navigating the practical mathematical challenges of everyday life. By grasping the underlying logic and exploring different solution methods, you develop a deeper appreciation for the elegance and utility of mathematics. Remember that mathematical proficiency is built through consistent practice and a genuine understanding of the processes involved. Don't hesitate to revisit the different methods presented here and apply them to similar problems to further solidify your understanding.
Latest Posts
Latest Posts
-
English Standard Paper 1 2022
Sep 20, 2025
-
Differentiate X 1 X 1
Sep 20, 2025
-
Difference Between Sterilization And Disinfection
Sep 20, 2025
-
Lemon Tree To Bear Fruit
Sep 20, 2025
-
What Is A Complex Sentance
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 5 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.