What Is 10 Of 100
candidatos
Sep 22, 2025 · 5 min read
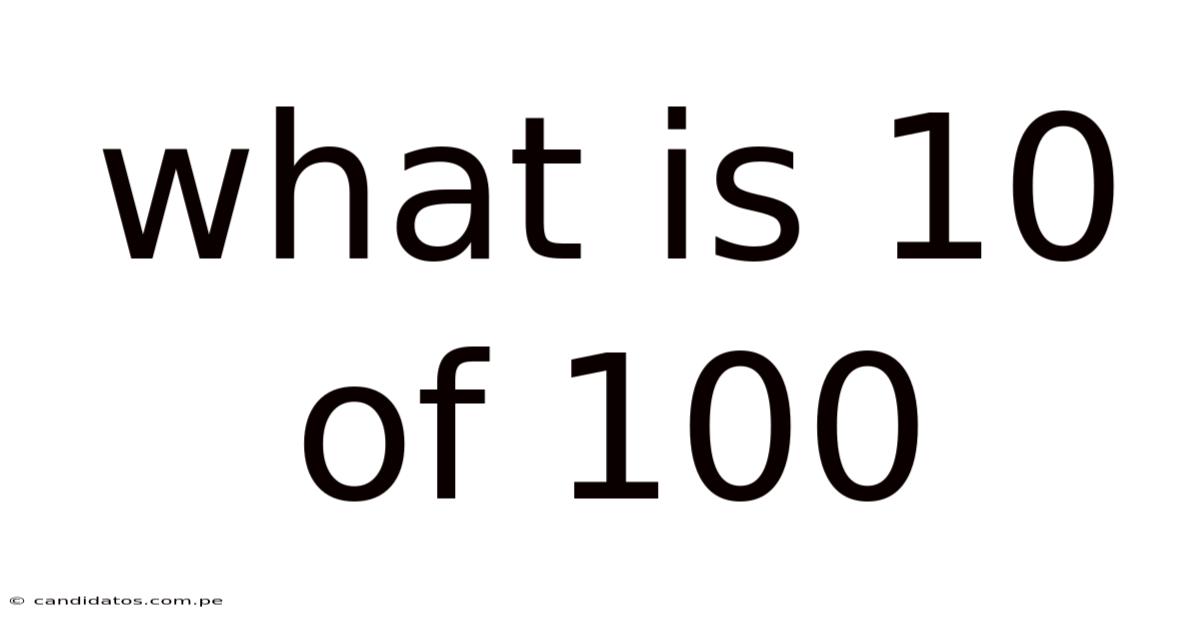
Table of Contents
What is 10 of 100? Unpacking Percentages, Fractions, and Ratios
Understanding the relationship between 10 and 100 is fundamental to grasping basic mathematical concepts. This seemingly simple question, "What is 10 of 100?", opens the door to exploring percentages, fractions, ratios, and their practical applications in everyday life. This article will delve into this seemingly simple query, providing a comprehensive explanation suitable for learners of all levels, from elementary school students to those seeking a refresher on foundational mathematical principles.
Introduction: Understanding the Basics
At its core, the question "What is 10 of 100?" asks us to determine the portion or part that 10 represents when compared to the whole, which is 100. This can be expressed in several ways, each offering a unique perspective on the same relationship. We'll explore these different representations, starting with the most intuitive: fractions.
Fractions: Representing Parts of a Whole
The simplest way to represent 10 out of 100 is as a fraction: 10/100. A fraction expresses a part of a whole, where the top number (numerator) indicates the part, and the bottom number (denominator) indicates the whole. In this case, 10 is the part, and 100 is the whole.
This fraction can be simplified by finding the greatest common divisor (GCD) of 10 and 100, which is 10. Dividing both the numerator and denominator by 10, we get:
10/100 = 1/10
This simplified fraction, 1/10, means that 10 out of 100 is equivalent to one-tenth of the whole. This is a crucial understanding because it lays the foundation for comprehending percentages and ratios.
Percentages: Expressing Parts per Hundred
A percentage is simply a fraction expressed as parts per hundred. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." To convert the fraction 10/100 to a percentage, we simply multiply the fraction by 100% :
(10/100) * 100% = 10%
Therefore, 10 out of 100 is equal to 10% (ten percent). This means that 10 represents 10 parts out of every 100 parts. Percentages are widely used to represent proportions, such as discounts, tax rates, and test scores, making them a vital tool for everyday calculations.
Ratios: Comparing Two Quantities
A ratio compares two quantities. In the context of 10 out of 100, we can express the ratio as 10:100. This reads as "10 to 100." Like fractions, ratios can be simplified by dividing both sides by their GCD (10):
10:100 = 1:10
This simplified ratio, 1:10, means that for every one part, there are ten parts in total. Ratios are frequently used in various fields, including cooking (e.g., mixing ingredients), scaling models, and comparing different data sets.
Visualizing 10 of 100: Practical Examples
Let's consider several practical examples to solidify our understanding of 10 out of 100:
-
A Test Score: If a test has 100 questions, and a student answers 10 correctly, their score is 10/100, or 10%. This represents a relatively low score, indicating that significant improvement is needed.
-
A Discount: A store offers a 10% discount on an item. If the original price is $100, the discount amount is 10% of $100, which is $10. The final price after the discount will be $90.
-
Survey Results: In a survey of 100 people, 10 responded positively to a particular question. This means that 10% of the respondents gave a positive response.
-
Probability: If there are 100 equally likely outcomes, and 10 of those outcomes represent a specific event, the probability of that event occurring is 10/100, or 10%.
These examples illustrate how the concept of 10 out of 100 translates to practical situations, showing the versatility of percentages, fractions, and ratios in representing parts of a whole.
Further Exploration: Expanding the Concept
The relationship between 10 and 100 can be further explored by considering its application in:
-
Decimal Representation: The fraction 10/100 can also be expressed as a decimal: 0.1. Decimals are another way to represent parts of a whole, often used in more complex calculations.
-
Proportions: The relationship between 10 and 100 can be described as a proportion. Proportions are mathematical statements that equate two ratios. For instance, 10/100 = x/200 can be solved to find the value of 'x' (which would be 20).
-
Scale Models: Architects and engineers frequently use ratios and proportions to create scale models. A 1:10 scale means that 1 unit on the model represents 10 units in reality. This same principle applies to maps, where a scale may be 1:100,000, meaning that 1 cm on the map represents 100,000 cm (or 1 kilometer) in real life.
-
Data Analysis: In data analysis, percentages and ratios are essential tools for summarizing and interpreting data sets. For example, we might use percentages to describe the proportion of respondents who prefer a specific product or to represent changes over time.
Frequently Asked Questions (FAQ)
Q: What is the difference between a fraction, a percentage, and a ratio?
A: While all three represent parts of a whole or comparisons between quantities, they are expressed differently. A fraction uses a numerator and denominator (e.g., 10/100). A percentage expresses a fraction as parts per hundred (e.g., 10%). A ratio compares two quantities (e.g., 10:100).
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, multiply the fraction by 100%. For example, 10/100 * 100% = 10%.
Q: How do I convert a percentage to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 10% = 10/100 = 1/10.
Q: What are some real-world applications of understanding 10 out of 100?
A: Real-world applications are abundant and include calculating discounts, interpreting test scores, understanding survey results, calculating probabilities, and working with scale models or maps.
Conclusion: Mastering the Fundamentals
Understanding the relationship between 10 and 100 is a cornerstone of basic mathematics. By grasping the concepts of fractions, percentages, and ratios, you develop a solid foundation for more advanced mathematical concepts. The ability to express and interpret these relationships is crucial for navigating various aspects of daily life, from personal finance to professional endeavors. Remember that consistent practice and application are key to mastering these fundamental principles. Continue exploring these concepts through further examples and problems to solidify your understanding and unlock the power of numbers!
Latest Posts
Latest Posts
-
Hsc Standard Maths Formula Sheet
Sep 22, 2025
-
8 20 As A Percentage
Sep 22, 2025
-
Essential Maths 10 And 10a
Sep 22, 2025
-
Botanical Name Of Lemon Plant
Sep 22, 2025
-
Function Of The Integral Protein
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.