8 20 As A Percentage
candidatos
Sep 22, 2025 · 5 min read
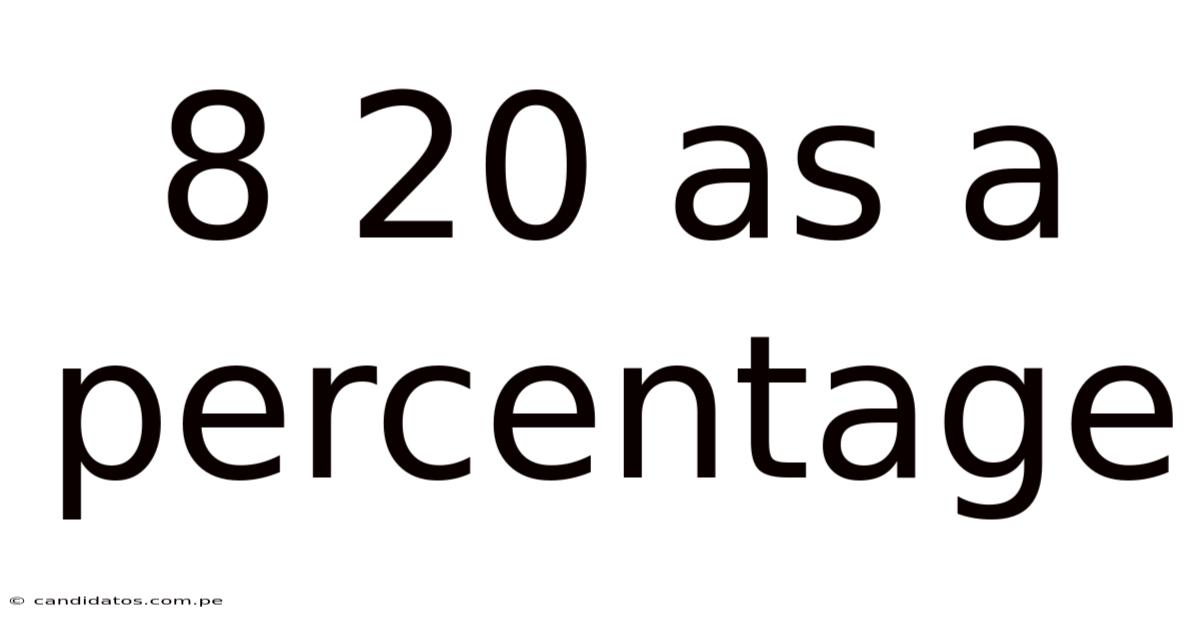
Table of Contents
Decoding 8/20 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve deep into converting fractions, specifically the fraction 8/20, into a percentage, providing a step-by-step guide, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll move beyond a simple answer and equip you with a robust understanding of percentage calculations.
Understanding Fractions and Percentages
Before diving into the specifics of 8/20, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of parts, and the numerator shows how many of those parts are being considered.
A percentage, denoted by the symbol %, represents a fraction where the denominator is always 100. It signifies "per hundred" or "out of one hundred". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or the simplified fraction 1/2.
Converting 8/20 to a Percentage: A Step-by-Step Guide
Converting the fraction 8/20 to a percentage involves a simple two-step process:
Step 1: Convert the fraction to a decimal.
To do this, we divide the numerator (8) by the denominator (20):
8 ÷ 20 = 0.4
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.4 x 100 = 40%
Therefore, 8/20 is equivalent to 40%.
Alternative Methods for Conversion
While the above method is straightforward, there are alternative approaches to reach the same result:
Method 1: Simplifying the Fraction First
We can simplify the fraction 8/20 before converting it to a decimal. Both the numerator and the denominator are divisible by 4:
8 ÷ 4 = 2 20 ÷ 4 = 5
This simplifies the fraction to 2/5. Now, we divide the numerator by the denominator:
2 ÷ 5 = 0.4
Then, we convert the decimal to a percentage:
0.4 x 100 = 40%
This method demonstrates that simplifying the fraction beforehand can sometimes make the calculation easier.
Method 2: Using Proportions
We can set up a proportion to solve for the percentage:
8/20 = x/100
To solve for x (the percentage), we cross-multiply:
20x = 800
x = 800 ÷ 20
x = 40
Therefore, x = 40%, confirming our previous results. This method highlights the proportional relationship between fractions and percentages.
The Mathematical Principle Behind Percentage Conversion
The core mathematical principle underlying percentage conversion lies in the concept of equivalent fractions. All the methods described above essentially involve finding an equivalent fraction with a denominator of 100. This equivalent fraction directly represents the percentage. The process of dividing the numerator by the denominator and multiplying by 100 achieves this conversion efficiently.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial for numerous real-world applications, including:
- Financial calculations: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Data analysis: Interpreting statistical data, such as survey results, economic indicators, and scientific measurements.
- Academic assessments: Determining grades based on scores, understanding test performance, and analyzing academic progress.
- Everyday situations: Calculating tips in restaurants, understanding sale prices, and comparing different offers.
Mastering percentage calculations empowers you to make informed decisions in various aspects of your life.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, any fraction can be converted to a percentage by following the steps outlined above. Even if the resulting percentage is a decimal or a very large number, the process remains the same.
Q2: What if the fraction is an improper fraction (numerator > denominator)?
A2: The process remains the same. Convert the improper fraction to a decimal by dividing the numerator by the denominator, then multiply by 100 to obtain the percentage. The resulting percentage will be greater than 100%.
Q3: How do I convert a percentage back to a fraction?
A3: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 60% becomes 60/100, which simplifies to 3/5.
Q4: Are there any online calculators or tools to help with percentage conversions?
A4: Yes, many online calculators are readily available to perform percentage conversions quickly and efficiently. These tools can be particularly helpful for more complex calculations or for checking your work. However, understanding the underlying principles remains crucial.
Q5: What are some common percentage errors to avoid?
A5: Common errors include incorrect decimal placement when converting between decimals and percentages, forgetting to multiply by 100 when converting decimals to percentages, and incorrectly interpreting percentage increases or decreases. Carefully review each step of the process to avoid these mistakes.
Conclusion: Mastering Percentages
Converting 8/20 to a percentage, resulting in 40%, is a simple yet fundamental skill. This article has explored multiple methods for this conversion, explained the underlying mathematical principles, and highlighted the widespread applications of percentage calculations in daily life. By understanding these concepts, you are equipped not only to solve specific percentage problems but also to confidently approach various mathematical and real-world challenges involving fractions and percentages. Remember to practice regularly to solidify your understanding and build your confidence in tackling percentage problems of any complexity. The ability to effortlessly convert fractions to percentages and vice versa is a valuable asset in numerous academic and professional contexts.
Latest Posts
Latest Posts
-
Convert 1 96 M To Feet
Sep 22, 2025
-
Candle Burning In The Dark
Sep 22, 2025
-
18 60 As A Percentage
Sep 22, 2025
-
Times Table 1 To 50
Sep 22, 2025
-
Echidna Vs Porcupine Vs Hedgehog
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 8 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.