Is 3/4 Greater Than 2/3
candidatos
Sep 22, 2025 · 6 min read
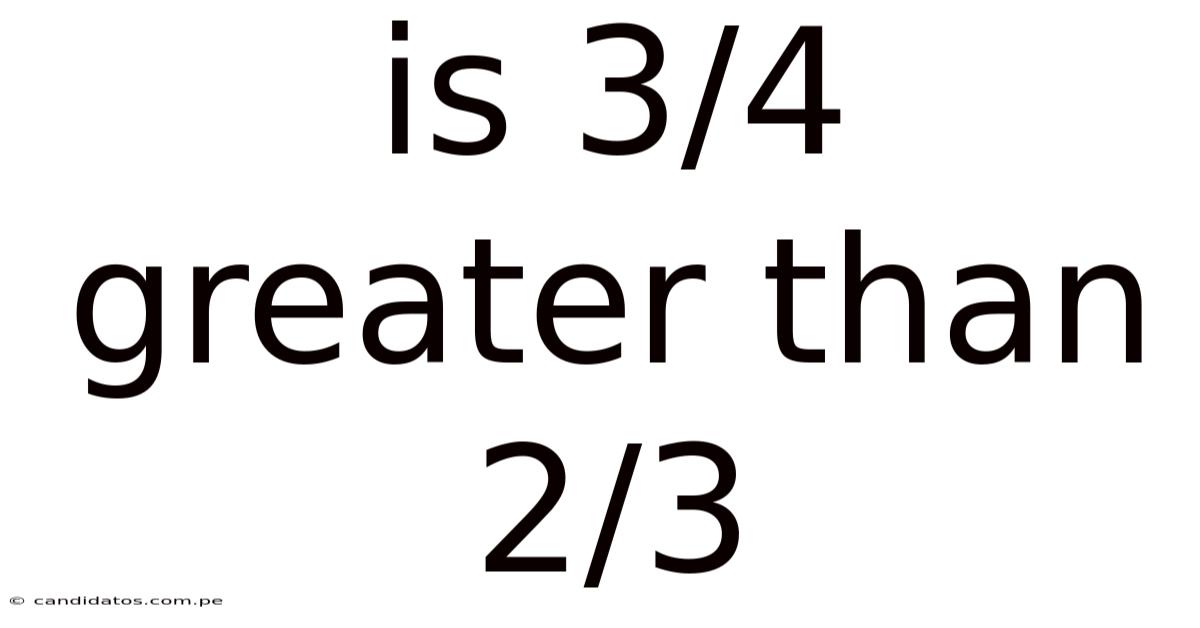
Table of Contents
Is 3/4 Greater Than 2/3? A Deep Dive into Fraction Comparison
Is 3/4 greater than 2/3? This seemingly simple question opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. While the answer itself is straightforward, exploring the various methods to compare fractions provides valuable insights into mathematical reasoning and problem-solving skills. This article will not only answer the question definitively but also equip you with the tools to compare any two fractions confidently.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's revisit the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3 and the denominator is 4. This means we have 3 out of 4 equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This involves converting both fractions so they have the same denominator. Once the denominators are the same, we can directly compare the numerators. The fraction with the larger numerator is the larger fraction.
Let's apply this method to compare 3/4 and 2/3:
-
Find the Least Common Multiple (LCM): The LCM of 4 and 3 is 12. This is the smallest number that both 4 and 3 divide into evenly.
-
Convert the fractions:
- To convert 3/4 to a fraction with a denominator of 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
- To convert 2/3 to a fraction with a denominator of 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
Compare the numerators: Now we have 9/12 and 8/12. Since 9 > 8, we conclude that 9/12 > 8/12, and therefore, 3/4 > 2/3.
Method 2: Converting to Decimals
Another approach involves converting the fractions to decimals. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator.
-
Convert to decimals:
- 3/4 = 0.75 (Divide 3 by 4)
- 2/3 = 0.666... (Divide 2 by 3 – this is a recurring decimal)
-
Compare the decimals: Since 0.75 > 0.666..., we can conclude that 3/4 > 2/3.
Method 3: Visual Representation
Visual aids can be extremely helpful, especially when explaining fractions to younger learners. Imagine two identical pizzas.
- One pizza is cut into four equal slices, and you eat three of them (3/4).
- The other pizza is cut into three equal slices, and you eat two of them (2/3).
By visually comparing the amount of pizza eaten, it’s clear that eating 3/4 of a pizza is more than eating 2/3 of a pizza. This visual representation reinforces the conclusion that 3/4 > 2/3.
Method 4: Cross-Multiplication
Cross-multiplication offers a quick way to compare two fractions. This method works by multiplying the numerator of one fraction by the denominator of the other and vice-versa.
-
Cross-multiply:
- Multiply the numerator of 3/4 (3) by the denominator of 2/3 (3): 3 x 3 = 9
- Multiply the numerator of 2/3 (2) by the denominator of 3/4 (4): 2 x 4 = 8
-
Compare the results: Since 9 > 8, we conclude that 3/4 > 2/3.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is crucial for various aspects of mathematics and real-world applications. From baking and cooking (measuring ingredients) to calculating proportions and percentages, understanding fraction comparison is a fundamental skill. Moreover, mastering this concept builds a solid foundation for more advanced mathematical concepts like algebra and calculus.
Beyond the Basics: Extending Fraction Comparison Skills
While the methods described above are sufficient for comparing simple fractions, understanding more advanced concepts enhances your mathematical proficiency.
-
Improper Fractions and Mixed Numbers: Improper fractions (where the numerator is greater than or equal to the denominator) and mixed numbers (a combination of a whole number and a fraction) require extra steps before comparison. Converting improper fractions to mixed numbers, or vice versa, often simplifies the comparison process.
-
Comparing More Than Two Fractions: When comparing more than two fractions, the common denominator method remains the most effective approach. Find the LCM of all the denominators, convert all fractions to this common denominator, and then compare the numerators.
-
Fractions with Negative Numerators or Denominators: Remember that negative fractions follow the same comparison rules, but the magnitude of the fraction's value changes. For example, -1/2 is greater than -3/4 because it's closer to 0 on the number line.
-
Equivalent Fractions: Recognizing equivalent fractions (fractions that represent the same value, such as 1/2 and 2/4) is crucial for simplification and efficient comparison.
Frequently Asked Questions (FAQ)
Q1: Why is finding a common denominator the most reliable method?
A1: Finding a common denominator ensures that we are comparing "like units." Just like we can't directly compare apples and oranges, we cannot directly compare fractions with different denominators without converting them to a common denominator first.
Q2: Can I always use decimal conversion to compare fractions?
A2: While decimal conversion is often a convenient method, it can be less accurate for fractions with recurring decimals (like 2/3). Rounding off the decimal can lead to slight inaccuracies in the comparison.
Q3: Is cross-multiplication always accurate?
A3: Yes, cross-multiplication is a reliable method for comparing two fractions. It's a shortcut derived from the common denominator method.
Q4: How can I improve my skills in comparing fractions?
A4: Practice is key! Work through various examples, including those involving improper fractions, mixed numbers, and negative fractions. Visual aids and real-world applications can enhance your understanding and retention.
Conclusion
The answer to the question "Is 3/4 greater than 2/3?" is a resounding yes. However, the journey to arrive at this answer is more significant than the answer itself. Mastering fraction comparison equips you with a valuable mathematical skill applicable in numerous contexts. By understanding and employing the various methods discussed – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – you'll develop a strong foundation for tackling more complex mathematical problems and confidently navigating the world of numbers. Remember that practice and a persistent curiosity will unlock your full mathematical potential.
Latest Posts
Latest Posts
-
18 Cm Converted To Inches
Sep 22, 2025
-
Word That Has 12 Letters
Sep 22, 2025
-
1 16 As A Percentage
Sep 22, 2025
-
Difference Between River And Creek
Sep 22, 2025
-
1 1 8 In Fraction
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Greater Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.