1 16 As A Percentage
candidatos
Sep 22, 2025 · 5 min read
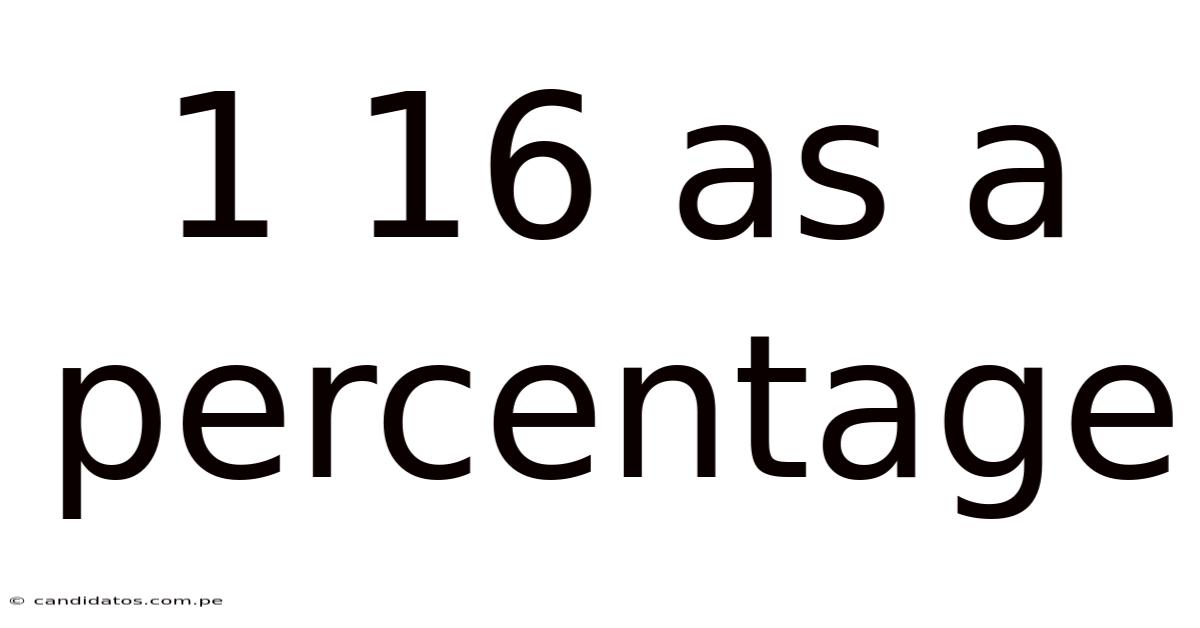
Table of Contents
Understanding 1/16 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, applicable across various fields from finance to cooking. This comprehensive guide delves into the conversion of the fraction 1/16 into a percentage, explaining the process step-by-step and exploring related concepts. We'll also tackle common misconceptions and answer frequently asked questions, ensuring you gain a solid grasp of this important topic. This article will cover the conversion method, its applications, and provide practical examples to solidify your understanding.
Introduction: Why is Understanding Percentages Important?
Percentages are a crucial tool for expressing proportions and comparisons. Whether calculating discounts, understanding interest rates, interpreting statistical data, or working with recipes, the ability to convert fractions to percentages and vice-versa is invaluable. This article focuses on the seemingly simple fraction 1/16, illustrating the broader principles applicable to any fraction-to-percentage conversion. Mastering this will empower you to tackle more complex scenarios with confidence.
Converting 1/16 to a Percentage: A Step-by-Step Guide
The core principle behind converting a fraction to a percentage involves transforming the fraction into an equivalent decimal and then multiplying by 100. Let's break down the process for 1/16:
Step 1: Perform the Division
The fraction 1/16 represents 1 divided by 16. Performing this division gives us the decimal equivalent:
1 ÷ 16 = 0.0625
Step 2: Multiply by 100
To convert the decimal to a percentage, multiply the result by 100:
0.0625 x 100 = 6.25
Step 3: Add the Percentage Symbol
Finally, add the percentage symbol (%) to indicate that the value represents a percentage:
6.25%
Therefore, 1/16 is equal to 6.25%.
Understanding the Process: A Deeper Dive
The conversion process hinges on the understanding that a percentage is simply a fraction with a denominator of 100. When we multiply a decimal by 100, we are essentially scaling the decimal up to express it as a fraction out of 100.
Let's illustrate this with our example:
- We started with the fraction 1/16.
- We found the decimal equivalent to be 0.0625.
- Multiplying by 100 is equivalent to multiplying the fraction by 100/1: (1/16) * (100/1) = 100/16.
- Simplifying this fraction gives us 25/4, which, when converted to a decimal, is 6.25. This confirms our earlier calculation.
This illustrates the fundamental link between fractions, decimals, and percentages. They are all different ways of representing the same proportional value.
Practical Applications of 1/16 as a Percentage
Understanding 1/16 as 6.25% has practical implications in various scenarios:
-
Measurement and Scaling: Imagine you're working on a scale model. If the model is 1/16th the size of the original, you can quickly understand that each part of the model represents 6.25% of the original object's size.
-
Finance and Budgeting: If a budget allows for 1/16th of a total amount to be spent on a particular item, this translates to a 6.25% allocation.
-
Data Analysis: If a survey shows 1/16th of respondents prefer a particular option, this represents a 6.25% preference rate.
-
Cooking and Baking: Recipes sometimes use fractional measurements. Understanding the percentage equivalent can help in scaling recipes up or down.
-
Probability and Statistics: Probability is often expressed as a fraction. Converting this fraction to a percentage can make it easier to interpret the likelihood of an event.
Common Misconceptions about Fraction-to-Percentage Conversions
Several common mistakes can occur when converting fractions to percentages:
-
Forgetting to multiply by 100: This is a frequent error. Remember that multiplying by 100 is crucial for expressing the value as a percentage.
-
Incorrect decimal division: Ensure accuracy when dividing the numerator by the denominator to obtain the decimal equivalent.
-
Rounding errors: While rounding might be necessary for practicality, be mindful of potential inaccuracies introduced by rounding during the calculation. It's always best to use the full decimal value before multiplying by 100 whenever possible.
Beyond 1/16: Generalizing the Conversion Process
The method described above is applicable to converting any fraction into a percentage. The steps remain the same:
- Divide the numerator by the denominator to find the decimal equivalent.
- Multiply the decimal by 100.
- Add the percentage symbol (%).
For example, let's convert 3/8 to a percentage:
- 3 ÷ 8 = 0.375
- 0.375 x 100 = 37.5
- Therefore, 3/8 = 37.5%
Working with Mixed Numbers
Mixed numbers (e.g., 1 1/2) require an extra step:
- Convert the mixed number into an improper fraction. For 1 1/2, this would be 3/2.
- Follow the standard fraction-to-percentage conversion steps. 3/2 = 1.5; 1.5 x 100 = 150%, therefore 1 1/2 = 150%.
Frequently Asked Questions (FAQ)
Q: What is the simplest way to remember how to convert a fraction to a percentage?
A: Remember that a percentage is just a fraction out of 100. Divide the numerator by the denominator, then multiply by 100.
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators can perform the division and multiplication necessary for this conversion.
Q: Are there any online tools to help with fraction-to-percentage conversions?
A: Yes, many websites and apps offer fraction-to-percentage converters. However, understanding the underlying process is crucial for problem-solving beyond simple conversions.
Q: Why is it important to understand this concept beyond simple calculations?
A: Understanding fraction-to-percentage conversions builds a foundation for more advanced mathematical concepts in areas like statistics, finance, and data analysis.
Q: What if I have a very large fraction? Does the process change?
A: No, the process remains the same regardless of the size of the fraction. However, for extremely large fractions, you might need to use a calculator to perform the division accurately.
Conclusion: Mastering the Art of Percentage Conversions
Converting 1/16 to a percentage, resulting in 6.25%, is more than just a simple mathematical exercise. It demonstrates a fundamental skill that is widely applicable in various aspects of life. Understanding the underlying principles, practicing the steps, and recognizing potential pitfalls will empower you to confidently tackle similar conversions and apply this knowledge to real-world problems. This understanding is not just about numbers; it's about understanding proportions and relationships, a skill vital for success in various fields. By mastering this seemingly simple conversion, you open the door to a broader understanding of mathematics and its practical applications. Remember to practice regularly and apply this knowledge to various scenarios to solidify your understanding.
Latest Posts
Latest Posts
-
Experiment Of Rate Of Reaction
Sep 22, 2025
-
1 10 000 In Words
Sep 22, 2025
-
Bachelor Of Biodiversity And Conservation
Sep 22, 2025
-
How Long Do Budgies Live
Sep 22, 2025
-
What Is The Accounting Equation
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 16 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.