Integrate X 2 1 X
candidatos
Sep 20, 2025 · 5 min read
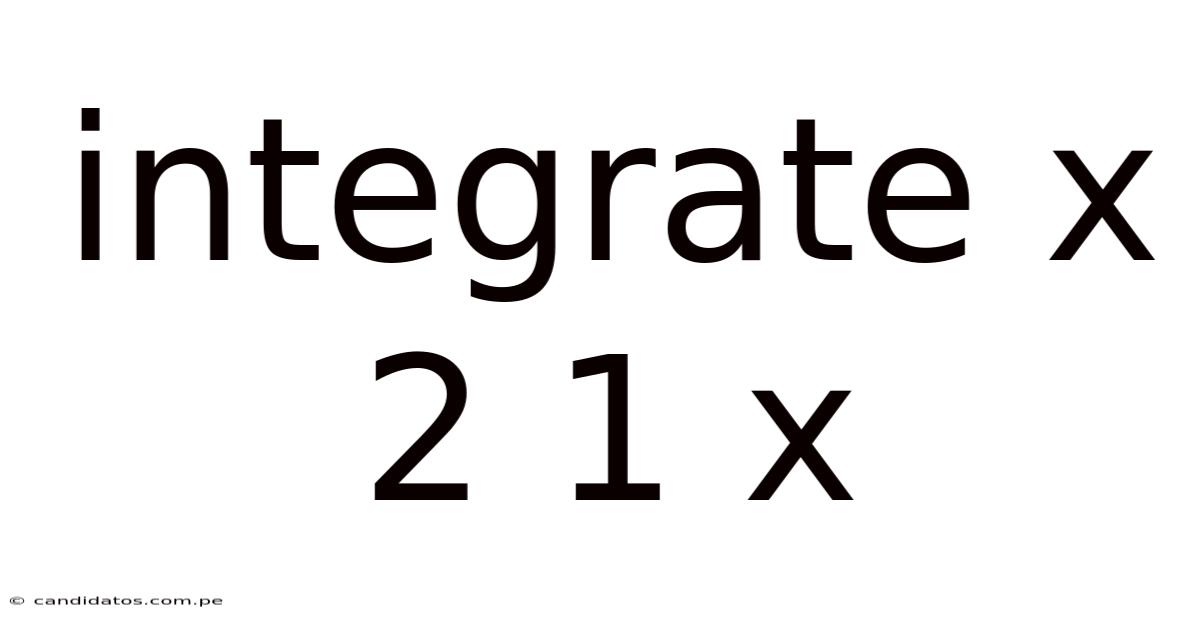
Table of Contents
Decoding the Mystery: A Deep Dive into the Integral of x²/(1+x)
The seemingly simple expression ∫x²/(1+x) dx can initially appear daunting. This integral, a cornerstone of calculus, requires a blend of algebraic manipulation, strategic substitution, and a solid understanding of integration techniques. This comprehensive guide will unravel the intricacies of solving this integral, providing a step-by-step process, exploring underlying mathematical principles, and addressing frequently asked questions. By the end, you'll not only understand how to solve this specific integral but also gain a broader appreciation for integral calculus and its applications.
Introduction: Why This Integral Matters
The integral ∫x²/(1+x) dx isn't just a random problem; it represents a class of integrals involving rational functions – fractions where both the numerator and denominator are polynomials. Mastering techniques to solve these integrals is crucial in various fields, including:
- Physics: Calculating work done by a variable force, analyzing trajectories of moving objects, and solving problems in fluid dynamics.
- Engineering: Determining areas, volumes, and centroids of complex shapes, crucial for designing structures and machinery.
- Economics: Modeling growth rates, calculating present values of future cash flows, and optimizing resource allocation.
- Probability and Statistics: Evaluating probability distributions and statistical moments.
This particular integral, while seemingly simple, demands more than a straightforward application of the power rule. It necessitates a strategic approach to simplify the integrand before integration.
Method 1: Polynomial Long Division
The most efficient approach to tackle this integral involves polynomial long division. This technique simplifies the integrand, transforming it into a more manageable form for integration.
Step 1: Polynomial Long Division
Divide the numerator (x²) by the denominator (1+x):
x - 1
1+x | x² + 0x + 0
x² + x
-------
-x + 0
-x - 1
-------
1
This division yields a quotient of x - 1 and a remainder of 1. Therefore, we can rewrite the integrand as:
x²/(1+x) = x - 1 + 1/(1+x)
Step 2: Integration
Now, we integrate each term separately:
∫x²/(1+x) dx = ∫(x - 1 + 1/(1+x)) dx
Applying the power rule and the integral of 1/u du = ln|u| + C (where u = 1+x), we get:
∫x²/(1+x) dx = (x²/2) - x + ln|1+x| + C
Therefore, the solution to the integral is (x²/2) - x + ln|1+x| + C, where C is the constant of integration.
Method 2: Substitution (A less efficient but instructive approach)
While polynomial long division is the preferred method, we can also explore solving this integral through substitution. This approach, though lengthier, provides valuable insights into alternative integration techniques.
Step 1: Substitution
Let's try the substitution u = 1+x. This implies that x = u - 1 and dx = du. Substituting these into the original integral, we obtain:
∫(u-1)²/u du = ∫(u² - 2u + 1)/u du
Step 2: Simplification
We can simplify the integrand by dividing each term in the numerator by u:
∫(u - 2 + 1/u) du
Step 3: Integration
Now, we integrate term by term:
∫(u - 2 + 1/u) du = (u²/2) - 2u + ln|u| + C
Step 4: Back-substitution
Finally, we substitute back u = 1+x to express the result in terms of x:
( (1+x)²/2 ) - 2(1+x) + ln|1+x| + C
This simplifies to:
(1 + 2x + x²)/2 - 2 - 2x + ln|1+x| + C = (x²/2) - x + ln|1+x| + C
Notice that this result is identical to the one obtained using polynomial long division. The constant of integration C absorbs the constant terms that arise from the simplification process.
A Deeper Look: The Significance of the Constant of Integration (C)
The constant of integration, C, is a crucial element in indefinite integrals. It represents a family of functions, all differing by a constant, that share the same derivative. This constant arises because the derivative of a constant is always zero. Therefore, when reversing the differentiation process (integration), we must account for the possibility of an arbitrary constant.
In practical applications, the value of C is often determined by initial conditions or boundary conditions associated with the problem. For instance, if we know the value of the integral at a specific point, we can solve for C.
Frequently Asked Questions (FAQs)
Q1: Can this integral be solved using other techniques?
While polynomial long division and substitution are the most straightforward methods, more advanced techniques like partial fraction decomposition could also be employed, although they would unnecessarily complicate the solution for this specific problem.
Q2: What if the denominator were (1-x) instead of (1+x)?
The process would be very similar. The only difference would be a change in sign in the logarithm term. The integral ∫x²/(1-x)dx would result in -(x²/2) - x - ln|1-x| + C.
Q3: How can I check my answer?
Differentiate your solution. If the derivative matches the original integrand (x²/(1+x)), your solution is correct. Remember to apply the chain rule when differentiating the logarithmic term.
Q4: What are some real-world applications of this type of integral?
This type of integral is fundamental to many applications, particularly in physics and engineering, such as calculating the work done by a force that varies with position, determining the area under a curve representing a non-linear function, or solving differential equations that describe physical systems.
Conclusion: Mastering the Art of Integration
Solving the integral ∫x²/(1+x) dx highlights the importance of strategic algebraic manipulation before applying integration techniques. Polynomial long division provides the most efficient solution, simplifying the integrand into a form readily integrable using the power rule and the logarithmic rule. While substitution is a viable approach, it often leads to a more complex process. Understanding this integral not only strengthens your calculus skills but also provides a foundation for tackling more complex integration problems encountered in various scientific and engineering disciplines. Remember to always check your answer by differentiating the result, and don't underestimate the importance of the constant of integration. Mastering these techniques will unlock a deeper understanding of the power and versatility of integral calculus.
Latest Posts
Latest Posts
-
Fruits That Begin With N
Sep 20, 2025
-
2x X 2x X 2x
Sep 20, 2025
-
Things That Rhyme With Do
Sep 20, 2025
-
Difference Between Sterilisation And Disinfection
Sep 20, 2025
-
5 Letter Word Start Sa
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Integrate X 2 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.