2x X 2x X 2x
candidatos
Sep 20, 2025 · 6 min read
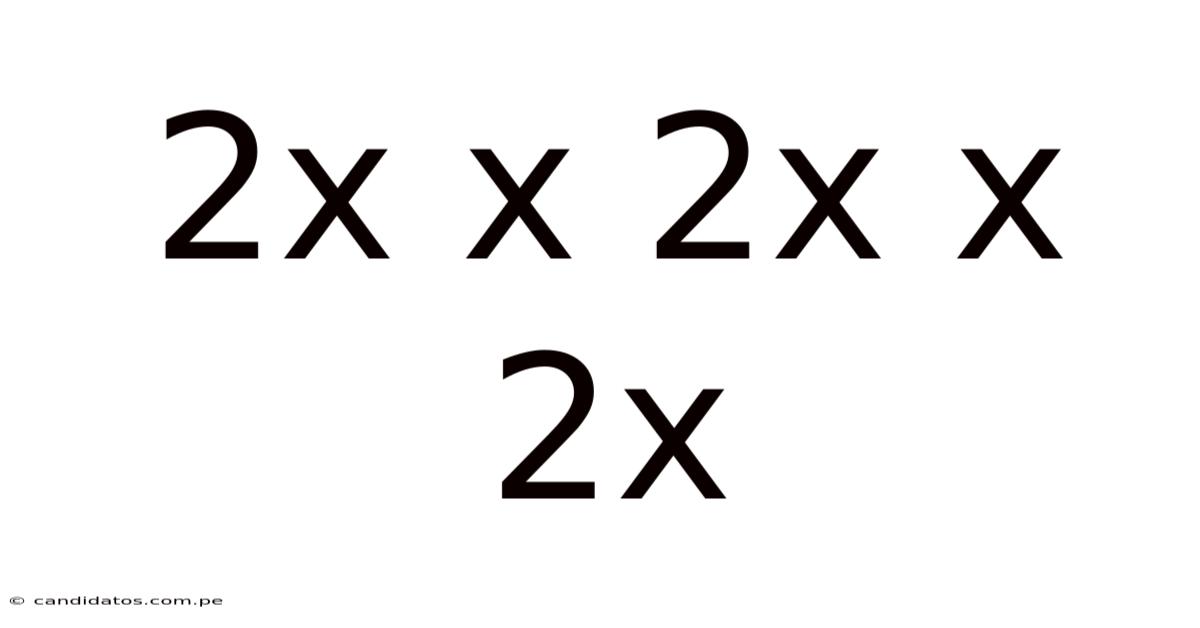
Table of Contents
Decoding 2x x 2x x 2x: Exponential Growth and its Real-World Applications
This article delves into the mathematical concept represented by "2x x 2x x 2x," exploring its meaning, implications, and practical applications across diverse fields. We will unravel the underlying principles of exponential growth, examining its power and potential impact, from biological systems to technological advancements and financial markets. Understanding this seemingly simple equation offers profound insights into the world around us.
Understanding Exponential Growth: Beyond Linear Progression
At its core, "2x x 2x x 2x" represents a process of exponential growth. Unlike linear growth, where a quantity increases by a constant amount over time, exponential growth involves an increase by a constant multiplier or rate. In this specific case, the multiplier is 2. Each "2x" signifies a doubling of the previous value. Therefore, the expression signifies a sequence of repeated doublings. It's crucial to understand that this type of growth is far more potent and rapid than linear growth.
Let's illustrate this with a simple example. Imagine you start with a single cell (x = 1). After one cycle of doubling (2x), you have 2 cells. After another doubling (2x x 2x), you have 4 cells. And finally, after the third doubling (2x x 2x x 2x), you have 8 cells. Notice how the growth accelerates dramatically. This is the hallmark of exponential growth – a rapid increase that becomes increasingly faster over time.
Mathematically, this can be expressed as 2³x, or 8x. The exponent (3 in this case) represents the number of doublings. Therefore, the equation "2x x 2x x 2x" simplifies to 8x, emphasizing the eightfold increase from the initial value.
Real-World Examples of 2x x 2x x 2x Growth Patterns:
The power of exponential growth is evident in numerous scenarios across various disciplines:
-
Biology: Cell division is a classic example. A single cell dividing into two, then four, eight, and so on, exemplifies exponential growth. This is fundamental to the growth and development of organisms. Similarly, the spread of viral infections can also follow an exponential pattern, initially appearing slow but rapidly escalating as each infected individual infects several others.
-
Technology: Moore's Law, a long-standing observation in the semiconductor industry, posits that the number of transistors on a microchip doubles approximately every two years. This exponential increase in computing power has driven remarkable technological advancements, from smartphones to supercomputers. The growth of the internet, with its expanding number of users and connected devices, also illustrates exponential growth.
-
Finance: Compound interest is another prime example. When interest earned is reinvested, the principal amount grows exponentially. This is why consistent saving and investment over time can yield significant returns, thanks to the power of compounding. Similarly, the growth of some investments, particularly those involved in emerging technologies, can also experience periods of exponential growth.
-
Social Media: The spread of viral content, memes, and trends on social media platforms frequently demonstrates exponential growth. A piece of content shared by a few individuals can quickly reach a massive audience as it’s shared and re-shared exponentially.
-
Natural Phenomena: Certain natural phenomena, such as the branching patterns of trees or the fractal geometry of coastlines, exhibit properties consistent with exponential growth. These natural patterns demonstrate that exponential growth is not merely a mathematical construct, but a fundamental principle governing various aspects of nature.
Mathematical Explanation and Implications:
The expression "2x x 2x x 2x" highlights the significance of exponents in mathematics. It illustrates how a relatively small base number (2 in this case), when raised to a higher power, can lead to a surprisingly large result. This concept has profound implications in various fields:
-
Predictive Modeling: Exponential growth models are crucial for predicting future trends in population growth, resource consumption, technological advancements, and disease outbreaks. Accurate predictions are essential for effective planning and resource management.
-
Data Analysis: Understanding exponential growth is vital for interpreting data and identifying patterns in various datasets, especially in fields like biology, finance, and epidemiology where exponential trends are commonplace.
-
Algorithm Design: Many efficient algorithms in computer science rely on the principles of exponential growth and decay to solve complex problems effectively.
-
Risk Assessment: Recognizing exponential growth patterns is crucial for evaluating risks associated with various phenomena, such as pandemics, environmental disasters, and financial crises. Early detection of exponential growth can enable timely interventions and risk mitigation strategies.
Beyond "2x x 2x x 2x": Generalizing Exponential Growth
The expression "2x x 2x x 2x" is a specific example. The general form of exponential growth is represented by the equation:
y = a * bˣ
Where:
- y is the final value.
- a is the initial value.
- b is the base (growth factor or multiplier).
- x is the number of periods of growth.
In our original example, a = x, b = 2, and x = 3. However, the principles of exponential growth remain the same regardless of the specific values of a and b. The key takeaway is that when b > 1, the function experiences exponential growth; when 0 < b < 1, it experiences exponential decay.
Frequently Asked Questions (FAQ)
-
What happens if 'x' is zero? If x = 0, then "2x x 2x x 2x" becomes 2⁰ x 2⁰ x 2⁰ = 1 x 1 x 1 = 1. This reflects the initial value before any growth occurs.
-
What if the multiplier isn't 2? The principle remains the same even if the multiplier is a different number (e.g., 3x x 3x x 3x). The growth will still be exponential, but the rate of growth will change accordingly. The general formula y = a * bˣ handles any base (b).
-
Can exponential growth continue indefinitely? In reality, exponential growth rarely continues indefinitely. Constraints such as resource limitations, competition, or regulatory factors often limit growth. Exponential growth is usually observed over a limited period.
-
How can I calculate exponential growth? The formula y = a * bˣ provides a simple way to calculate exponential growth. Substitute the values for the initial value (a), the growth factor (b), and the number of growth periods (x) to determine the final value (y).
Conclusion: Harnessing the Power of Exponential Growth
The seemingly simple expression "2x x 2x x 2x" unlocks a deep understanding of exponential growth – a powerful force shaping our world. From microscopic cell division to macroscopic technological advancements and financial markets, this concept is ubiquitous. Understanding its implications is not merely an academic exercise; it's a crucial tool for predicting future trends, interpreting data, designing algorithms, and making informed decisions across a wide range of fields. By appreciating the power and limitations of exponential growth, we can better navigate the complexities of our rapidly changing world and harness its potential for positive change. It’s vital to remember that while exponential growth offers incredible opportunities, it also presents significant challenges that require careful consideration and proactive management.
Latest Posts
Latest Posts
-
Christmas Tree Drawing For Kids
Sep 20, 2025
-
Map Of Australia And Antarctica
Sep 20, 2025
-
What Does Decreased By Mean
Sep 20, 2025
-
Maths Questions For Year 4
Sep 20, 2025
-
Kazakhstan Currency In Indian Rupees
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 2x X 2x X 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.