Integral Of 1 X 3
candidatos
Sep 16, 2025 · 6 min read
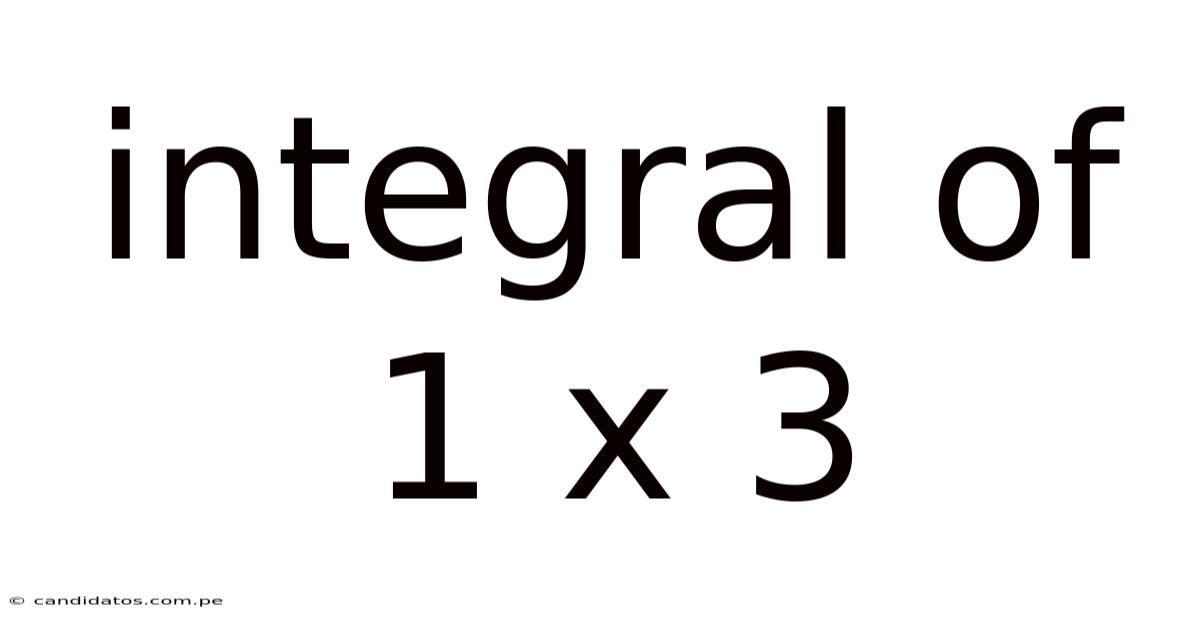
Table of Contents
Understanding and Solving the Integral of 1/(x³): A Comprehensive Guide
The integral of 1/x³, often written as ∫1/x³ dx, is a fundamental concept in calculus. This comprehensive guide will walk you through the process of solving this integral, exploring the underlying mathematical principles, and addressing common questions. Understanding this seemingly simple integral lays a crucial foundation for tackling more complex integration problems. We will cover the solution method, explore the underlying power rule, delve into the concept of indefinite integrals and constants of integration, and finally address frequently asked questions.
Understanding the Problem: ∫1/x³ dx
Before diving into the solution, let's clarify what we're dealing with. The expression ∫1/x³ dx represents the indefinite integral of the function f(x) = 1/x³. An indefinite integral finds a family of functions whose derivative is the given function. In simpler terms, we are looking for a function that, when differentiated, gives us 1/x³.
Applying the Power Rule of Integration
The key to solving this integral lies in the power rule of integration. The power rule states that the integral of xⁿ is (xⁿ⁺¹)/(n+1) + C, where n is any real number except -1, and C is the constant of integration. To apply this rule to our problem, we first need to rewrite 1/x³ as x⁻³.
Now we have: ∫x⁻³ dx
Applying the power rule:
- n in our case is -3.
- n + 1 becomes -3 + 1 = -2.
- Therefore, the integral is (x⁻²)/(-2) + C
Simplifying, we get: -1/(2x²) + C
Therefore, the indefinite integral of 1/x³ is -1/(2x²) + C.
Understanding the Constant of Integration (C)
The constant of integration, C, is crucial and often overlooked. It represents an entire family of functions. Remember, the derivative of a constant is always zero. Therefore, if you differentiate -1/(2x²) + C, + 100C, or -1/(2x²) + πC, you will always get back 1/x³. Each value of C represents a different function, all of which have the same derivative, 1/x³.
Visualizing the Integral: Geometric Interpretation
While we've solved the integral algebraically, it's beneficial to understand its geometric interpretation. The indefinite integral represents the family of antiderivatives. Each function in this family represents a curve on a graph. These curves are all vertical translations of each other, differing only by the value of the constant C. The constant C shifts the entire curve up or down along the y-axis.
Imagine plotting several functions of the form -1/(2x²) + C for different values of C. You’d see a series of curves, all with the same basic shape but shifted vertically. Each curve represents a possible antiderivative of 1/x³.
Definite Integrals and Boundaries
While our focus has been on indefinite integrals, it’s important to mention definite integrals. A definite integral has upper and lower limits of integration. For example:
∫(from a to b) 1/x³ dx
To solve a definite integral, we first find the indefinite integral, then evaluate it at the upper and lower limits and subtract the results. This gives us a numerical value representing the area under the curve of 1/x³ between the limits a and b. The constant of integration C cancels out when evaluating definite integrals.
Addressing Common Mistakes and Challenges
Several common mistakes can arise when working with integrals, particularly for beginners:
- Forgetting the Constant of Integration (C): This is perhaps the most frequent error. Always remember to include the constant of integration when dealing with indefinite integrals.
- Incorrect Application of the Power Rule: Ensure you're correctly adding 1 to the exponent and dividing by the new exponent. Pay close attention to negative exponents.
- Incorrect Simplification: After applying the power rule, carefully simplify the resulting expression. Many errors occur due to careless algebraic manipulation.
- Confusing Indefinite and Definite Integrals: Understand the difference between finding a family of functions (indefinite integral) and finding a numerical value representing an area (definite integral).
Advanced Considerations: Dealing with Singularities
The function 1/x³ has a singularity at x = 0. This means the function is undefined at x = 0. This singularity has implications for integration. When integrating over an interval that includes x = 0, the integral will be improper and requires special techniques to evaluate. These techniques often involve taking limits as the integration approaches the singularity.
In simple terms, you cannot directly integrate 1/x³ across an interval containing 0 because the area under the curve at that point becomes infinite.
Expanding Your Knowledge: Related Integrals and Techniques
Understanding the integral of 1/x³ lays the groundwork for tackling other similar integrals:
- Integrals of other power functions: The power rule applies to many other functions of the form xⁿ, allowing you to solve a wide variety of integration problems.
- Integration by substitution (u-substitution): This technique can simplify complex integrals by making a substitution that changes the variable of integration.
- Integration by parts: This is a powerful technique for integrating products of functions.
- Partial fraction decomposition: This method is useful for integrating rational functions (fractions involving polynomials).
Frequently Asked Questions (FAQ)
Q: What is the difference between integration and differentiation?
A: Differentiation finds the instantaneous rate of change of a function, while integration finds the area under the curve of a function. They are inverse operations; integration "undoes" differentiation.
Q: Why is the constant of integration important?
A: The constant of integration represents the family of antiderivatives. Each value of C represents a different function, all of which have the same derivative. It's essential for indefinite integrals.
Q: Can I solve the integral of 1/x³ using other methods?
A: While the power rule is the most straightforward method, you could potentially use techniques like integration by substitution or even geometric reasoning (although the latter becomes increasingly complex for more intricate functions). However, the power rule remains the most efficient and commonly used method for this specific integral.
Q: What happens if the limits of integration are negative?
A: The same principles apply. Remember to carefully evaluate the indefinite integral at both limits, paying attention to the signs. The area under the curve will still be calculated correctly, even with negative limits. The result may be a negative value, reflecting the fact that the function is below the x-axis in those regions.
Q: How can I improve my understanding of integration?
A: Consistent practice is crucial. Work through numerous problems, starting with simpler ones and gradually moving to more complex integrals. Utilize resources like textbooks, online tutorials, and practice exercises to build your understanding and skills.
Conclusion
Solving the integral of 1/x³ is a fundamental step in mastering calculus. By understanding the power rule of integration and the importance of the constant of integration, you can confidently tackle this and similar problems. Remember to practice regularly, and don't hesitate to consult resources and seek help when facing challenges. Mastering integration opens doors to a deeper understanding of mathematical modeling and problem-solving in various fields of science and engineering. The key is consistent effort and a patient approach to learning.
Latest Posts
Latest Posts
-
1 7 8 In Millimeters
Sep 16, 2025
-
Top Cat Benny The Ball
Sep 16, 2025
-
Male And Female Guinea Fowl
Sep 16, 2025
-
Ancient History Stage 6 Syllabus
Sep 16, 2025
-
3 8 Divided By 5
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.