3 8 Divided By 5
candidatos
Sep 16, 2025 · 5 min read
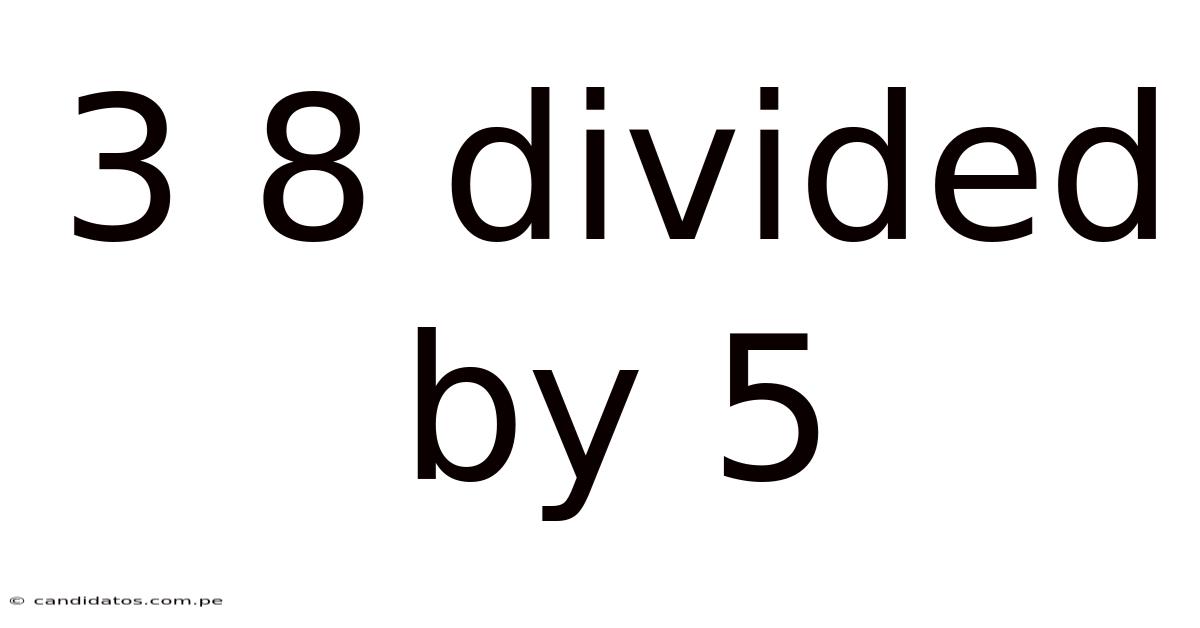
Table of Contents
Unveiling the Mystery: 38 Divided by 5 – A Deep Dive into Division
Dividing 38 by 5 might seem like a simple arithmetic problem, suitable only for elementary school students. However, a closer look reveals a rich tapestry of mathematical concepts, from basic division to understanding remainders and their implications in real-world applications. This comprehensive guide will not only show you how to solve 38 ÷ 5 but will also explore the underlying principles and demonstrate its relevance beyond the confines of a textbook.
Understanding the Basics of Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the problem 38 ÷ 5, we're asking: "How many times does 5 fit into 38?" The answer isn't a whole number, leading us into the realm of quotients and remainders.
Step-by-Step Solution: 38 ÷ 5
Let's break down the division process methodically:
-
Long Division: The most common method for solving this problem is long division. We set up the problem like this:
7 5 | 38 35 -- 3- We start by asking how many times 5 goes into 3 (the first digit of 38). It doesn't go in at all, so we move to the next digit.
- Now we ask how many times 5 goes into 38. 5 goes into 38 seven times (5 x 7 = 35). We write the 7 above the 8 in the dividend (38).
- We then subtract 35 from 38, leaving a remainder of 3.
-
Interpreting the Result: The quotient (the result of the division) is 7, and the remainder is 3. This means that 5 goes into 38 seven times with 3 left over. We can express this as:
- 38 ÷ 5 = 7 with a remainder of 3
- 38 = (5 x 7) + 3
-
Decimal Representation: We can also express the answer as a decimal. To do this, we continue the long division process by adding a decimal point and a zero to the remainder:
7.6 5 | 38.0 35 -- 30 30 -- 0- We bring down the zero and ask how many times 5 goes into 30. It goes in 6 times (5 x 6 = 30).
- Subtracting 30 from 30 leaves a remainder of 0. Therefore, the decimal representation of 38 ÷ 5 is 7.6.
Different Approaches to Division
While long division is the most common method, other approaches can be used, especially for simpler problems or to build a stronger conceptual understanding.
-
Repeated Subtraction: We can repeatedly subtract 5 from 38 until we reach a number less than 5. The number of times we subtract 5 represents the quotient, and the remaining number is the remainder.
38 - 5 = 33 33 - 5 = 28 28 - 5 = 23 23 - 5 = 18 18 - 5 = 13 13 - 5 = 8 8 - 5 = 3
We subtracted 5 seven times, resulting in a remainder of 3.
-
Fraction Representation: The problem can also be expressed as a fraction: 38/5. This fraction can be simplified or converted to a mixed number:
38/5 = 7 3/5 (This means 7 wholes and 3/5 of a whole)
This mixed number representation is equivalent to the quotient and remainder we found using long division.
The Significance of Remainders
The remainder in 38 ÷ 5 (which is 3) holds significant meaning and is not simply an insignificant leftover. It indicates that after dividing 38 into groups of 5, there are 3 items remaining that cannot be equally distributed. The context of the problem determines how to handle this remainder.
-
Real-world Examples: Imagine you have 38 candies to distribute equally among 5 friends. Each friend would receive 7 candies (the quotient), and you would have 3 candies left over (the remainder). You could either keep the remaining candies, share them unevenly, or perhaps buy more candies to distribute equally.
-
Rounding: Depending on the context, you might round the decimal representation (7.6) up or down. If you need whole numbers, rounding down would give you 7, while rounding up would give you 8.
Exploring the Relationship between Division, Multiplication, and Other Operations
Division is closely linked to multiplication. Division is essentially the inverse operation of multiplication. If we multiply the quotient (7) by the divisor (5), and add the remainder (3), we get back the original dividend (38). This demonstrates the fundamental relationship: (7 x 5) + 3 = 38.
This relationship also extends to other mathematical concepts like factors, multiples, and prime numbers. Understanding these connections is crucial for developing a solid mathematical foundation.
Expanding on the Concept: Working with Larger Numbers
The principles we've explored with 38 ÷ 5 apply to dividing any number by any other number. The process of long division remains the same, regardless of the size of the numbers involved. The only difference is that the calculations become more complex with larger numbers. For instance, solving 12345 ÷ 17 would require more steps, but the underlying logic remains unchanged.
Frequently Asked Questions (FAQs)
-
What if the remainder is 0? If the remainder is 0, it means the division is exact; the divisor is a factor of the dividend. For example, 35 ÷ 5 = 7 (remainder 0).
-
How do I handle larger remainders? Larger remainders are treated the same way as smaller ones. They represent the amount that is left over after the equal distribution.
-
Why is it important to understand remainders? Remainders are crucial in various fields, including engineering, computer science (especially in modular arithmetic), and everyday life scenarios involving distribution or sharing.
-
Can I use a calculator to solve this problem? Yes, a calculator is a useful tool for performing calculations, but understanding the underlying process is equally, if not more, important.
Conclusion: Beyond the Numbers
This in-depth exploration of 38 divided by 5 demonstrates that even seemingly simple arithmetic problems can offer profound insights into the beauty and logic of mathematics. The journey from basic division to understanding remainders, decimal representations, and the connection between different mathematical operations is a testament to the interconnectedness of mathematical concepts. Mastering these concepts not only improves your arithmetic skills but also builds a strong foundation for more advanced mathematical explorations. Remember, the goal is not just to find the answer (7.6), but to understand why that is the answer and how it relates to the broader world of mathematics and problem-solving.
Latest Posts
Latest Posts
-
Number Of Protons In Potassium
Sep 16, 2025
-
3v 1 Amp Power Supply
Sep 16, 2025
-
13 Squared 12 Squared
Sep 16, 2025
-
31 Out Of 50 Percentage
Sep 16, 2025
-
Meaning Of Inevitability In Hindi
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3 8 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.