9 12 As A Percent
candidatos
Sep 21, 2025 · 5 min read
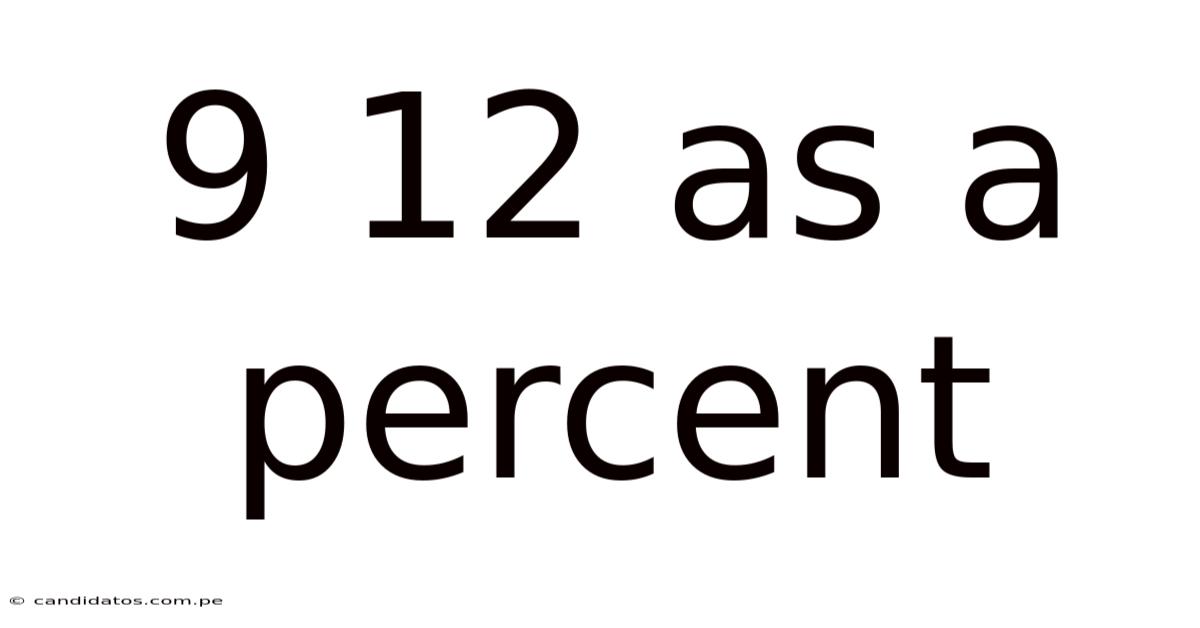
Table of Contents
9/12 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications ranging from calculating grades to understanding financial data. This comprehensive guide will walk you through the process of converting the fraction 9/12 into a percentage, explaining the underlying concepts and providing practical examples. We'll also explore related concepts and answer frequently asked questions to ensure a thorough understanding. This guide aims to be your definitive resource for mastering this essential mathematical conversion.
Understanding Fractions and Percentages
Before diving into the conversion of 9/12, let's briefly review the concepts of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of parts in the whole. For instance, in the fraction 9/12, 9 is the numerator and 12 is the denominator. This means we have 9 parts out of a total of 12 parts.
A percentage is a way of expressing a number as a fraction of 100. It's denoted by the symbol "%". For example, 50% means 50 out of 100, or 50/100. Percentages are widely used to represent proportions, rates, and changes in various contexts.
Converting 9/12 to a Percentage: Step-by-Step Guide
There are two primary methods to convert 9/12 to a percentage:
Method 1: Simplifying the Fraction First
This method involves simplifying the fraction to its lowest terms before converting it to a percentage. This simplifies the calculation and often leads to a more easily understandable result.
Step 1: Simplify the Fraction
Both the numerator (9) and the denominator (12) are divisible by 3. Dividing both by 3, we get:
9 ÷ 3 = 3 12 ÷ 3 = 4
Therefore, 9/12 simplifies to 3/4.
Step 2: Convert the Simplified Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator by the denominator:
3 ÷ 4 = 0.75
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.75 × 100 = 75%
Therefore, 9/12 is equal to 75%.
Method 2: Direct Conversion
This method involves directly converting the fraction to a decimal and then to a percentage without simplifying the fraction first.
Step 1: Convert the Fraction to a Decimal
Divide the numerator (9) by the denominator (12):
9 ÷ 12 = 0.75
Step 2: Convert the Decimal to a Percentage
Multiply the decimal by 100 and add the "%" symbol:
0.75 × 100 = 75%
As you can see, both methods yield the same result: 75%. The first method, however, is often preferred as it simplifies the calculations and makes it easier to grasp the underlying relationships between the numbers.
Understanding the Result: What Does 75% Mean?
75% means that 9 out of 12 represents three-quarters (3/4) of the whole. This is a significant proportion, indicating a substantial portion of the total. In various applications, understanding the magnitude of 75% is crucial for making informed decisions or interpretations. For instance, if 9 out of 12 students passed a test, it represents a 75% pass rate, indicating a generally successful outcome.
Practical Applications of Fraction-to-Percentage Conversion
Converting fractions to percentages has numerous practical applications across various fields:
- Academic Performance: Calculating grades and percentages of correct answers on tests or assignments.
- Financial Analysis: Determining profit margins, interest rates, and growth percentages.
- Data Analysis: Representing proportions and trends in data sets using percentages for clarity and ease of understanding.
- Everyday Life: Calculating discounts, sales tax, and tips.
Further Exploration: Working with Different Fractions
The process outlined above can be applied to any fraction. Here are some examples:
- 1/2: 1 ÷ 2 = 0.5 × 100 = 50%
- 2/5: 2 ÷ 5 = 0.4 × 100 = 40%
- 3/8: 3 ÷ 8 = 0.375 × 100 = 37.5%
Remember to always simplify the fraction to its lowest terms whenever possible to make the calculation easier and more efficient.
Frequently Asked Questions (FAQ)
Q: Can I convert a percentage back to a fraction?
A: Yes, you can. To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 75% is equivalent to 75/100, which simplifies to 3/4.
Q: What if the fraction results in a repeating decimal?
A: Some fractions, when converted to decimals, result in repeating decimals (e.g., 1/3 = 0.333...). In such cases, you can round the decimal to a certain number of decimal places before converting it to a percentage. The level of precision required will depend on the context of the problem.
Q: Are there any online tools or calculators to help with this conversion?
A: Yes, many online calculators and tools are available to perform fraction-to-percentage conversions. These tools can be helpful for quickly verifying results or performing conversions with more complex fractions.
Conclusion
Converting fractions to percentages is a crucial mathematical skill with wide-ranging applications. The process involves converting the fraction to a decimal by dividing the numerator by the denominator, then multiplying the decimal by 100 to obtain the percentage. Simplifying the fraction before conversion can often simplify the calculation. Understanding this process empowers you to interpret data, analyze proportions, and solve practical problems effectively. Remember to practice regularly to build your confidence and mastery of this fundamental mathematical concept. Through consistent practice and understanding the underlying principles, you'll be able to confidently tackle fraction-to-percentage conversions in various real-world scenarios.
Latest Posts
Latest Posts
-
Pvt Company Vs Public Company
Sep 22, 2025
-
5 23 As A Percentage
Sep 22, 2025
-
Word For Sad And Happy
Sep 22, 2025
-
Things That Start With Aa
Sep 22, 2025
-
Alphabet Number Chart 1 26
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 9 12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.