5 23 As A Percentage
candidatos
Sep 22, 2025 · 5 min read
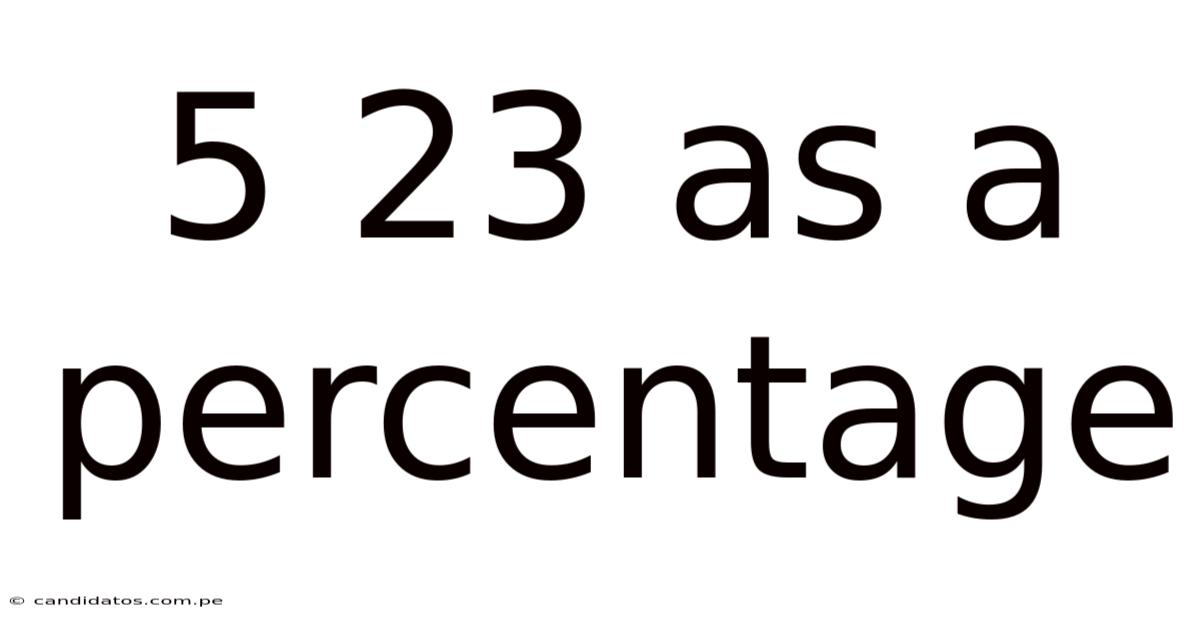
Table of Contents
5/23 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in a shop to understanding statistical data. This article provides a comprehensive guide on how to convert the fraction 5/23 into a percentage, explaining the process step-by-step and exploring the underlying mathematical principles. We'll also delve into practical applications and answer frequently asked questions to solidify your understanding.
Understanding Fractions and Percentages
Before diving into the conversion of 5/23, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of 100. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
The core principle behind converting a fraction to a percentage is to express the fraction as an equivalent fraction with a denominator of 100.
Converting 5/23 to a Percentage: Step-by-Step Guide
There are two main methods to convert 5/23 to a percentage:
Method 1: Using Division
This method involves dividing the numerator by the denominator and then multiplying the result by 100.
-
Divide the numerator by the denominator: 5 ÷ 23 ≈ 0.21739
-
Multiply the result by 100: 0.21739 × 100 = 21.739
-
Round to the desired precision: Depending on the level of accuracy needed, we can round the result. Rounding to one decimal place, we get 21.7%. Rounding to two decimal places, we get 21.74%.
Therefore, 5/23 is approximately 21.74%.
Method 2: Creating an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. While this method is conceptually straightforward, it's not always practical, especially when the denominator doesn't easily divide into 100.
-
Set up a proportion: We want to find x such that:
5/23 = x/100
-
Cross-multiply:
23x = 500
-
Solve for x:
x = 500/23 ≈ 21.739
-
Express as a percentage: x represents the percentage, so we have approximately 21.74%.
Understanding the Result: 21.74%
The result, 21.74%, signifies that 5 represents approximately 21.74% of 23. This means if you divide something into 23 equal parts and take 5 of those parts, you've taken approximately 21.74% of the whole.
Practical Applications of Fraction to Percentage Conversions
Converting fractions to percentages is crucial in various real-world scenarios:
-
Financial Calculations: Calculating interest rates, discounts, tax rates, and profit margins often involve converting fractions to percentages. For example, a 1/4 discount is equivalent to a 25% discount.
-
Statistical Analysis: Percentages are commonly used to represent data proportions in surveys, polls, and research studies. Converting fractions simplifies the interpretation of such data.
-
Everyday Life: Understanding percentages helps in comparing prices, determining tip amounts, and understanding proportions in recipes.
Beyond the Basics: Exploring Decimal Representation and Significant Figures
The decimal representation of 5/23 (approximately 0.21739) is also a valuable way to understand the fraction. This decimal shows the fraction's value as a proportion of one. Multiplying by 100 converts this proportion to a percentage.
The number of decimal places used (and thus, the level of precision in the percentage) depends on the context. For many practical purposes, rounding to one or two decimal places (21.7% or 21.74%) is sufficient. However, in scientific or engineering applications, more significant figures might be required to ensure accuracy. The concept of significant figures dictates the number of digits that carry meaning in a measurement or calculation.
Advanced Concepts: Understanding Errors and Approximations
When converting fractions to percentages, it's important to remember that the process often involves approximation, particularly when dealing with fractions that don't easily convert to a whole number percentage. The approximation inherent in rounding can introduce a small error. The magnitude of this error depends on the level of precision used. For example, using 21.7% introduces a larger error than using 21.74%, but the latter is still an approximation.
Frequently Asked Questions (FAQs)
Q: Why is it important to understand how to convert fractions to percentages?
A: Converting fractions to percentages is crucial for interpreting and communicating proportions effectively across various fields, making data easier to understand and compare.
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have the functionality to perform this conversion directly. Simply divide the numerator by the denominator and then multiply by 100.
Q: What if the fraction results in a repeating decimal when converted to a percentage?
A: Repeating decimals are common when converting fractions to percentages. In such cases, you'll need to decide on the appropriate level of precision (number of decimal places) for your application and round accordingly.
Q: How can I improve my understanding of fractions and percentages?
A: Practicing various conversion problems, exploring real-world examples, and utilizing online resources and educational materials can greatly improve your understanding.
Conclusion
Converting the fraction 5/23 to a percentage involves a straightforward process, primarily utilizing division and multiplication. The result, approximately 21.74%, represents the proportion of 5 relative to 23. This fundamental skill has far-reaching implications in various aspects of life, from everyday calculations to complex statistical analysis. Understanding the underlying principles, different methods of conversion, and the concept of approximation allows for accurate and effective use of percentages in various contexts. The ability to confidently convert fractions to percentages empowers you to interpret data, make informed decisions, and effectively communicate proportions in numerical form.
Latest Posts
Latest Posts
-
Drawing Of My Dream House
Sep 22, 2025
-
Number Line 0 To 1
Sep 22, 2025
-
Absolute Pressure Vs Gauge Pressure
Sep 22, 2025
-
M 2 To Mm 2
Sep 22, 2025
-
4 Letter Word Ending P
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 23 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.