18 60 As A Percentage
candidatos
Sep 22, 2025 · 5 min read
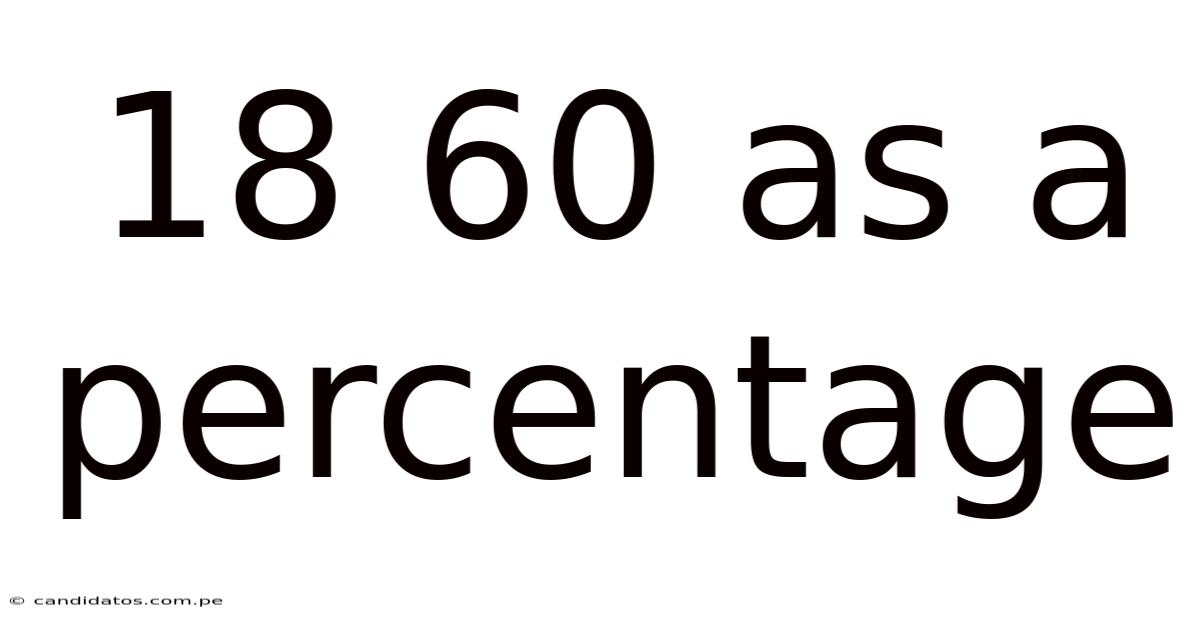
Table of Contents
Decoding 18/60 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in a store to understanding statistical data. This comprehensive guide will delve into the process of converting the fraction 18/60 into a percentage, explaining the underlying concepts and providing practical examples. We'll explore different methods, address common misconceptions, and provide additional resources to solidify your understanding. This article will also cover related concepts to help you build a robust understanding of percentage calculations.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). In the fraction 18/60, 18 is the numerator and 60 is the denominator. This means we are considering 18 parts out of a total of 60 parts.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," which means "out of 100." Therefore, a percentage is essentially a fraction with a denominator of 100. For example, 50% is equivalent to 50/100, which simplifies to 1/2.
Method 1: Simplifying the Fraction First
The most efficient way to convert 18/60 to a percentage often involves simplifying the fraction before converting it to a percentage. This makes the calculation easier and reduces the risk of errors.
-
Find the Greatest Common Divisor (GCD): The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. In this case, the GCD of 18 and 60 is 6.
-
Simplify the Fraction: Divide both the numerator and the denominator by the GCD:
18 ÷ 6 = 3 60 ÷ 6 = 10
This simplifies the fraction to 3/10.
-
Convert to a Decimal: Divide the numerator by the denominator:
3 ÷ 10 = 0.3
-
Convert to a Percentage: Multiply the decimal by 100 and add the percentage sign:
0.3 × 100 = 30%
Therefore, 18/60 is equal to 30%.
Method 2: Direct Conversion to Percentage
Alternatively, you can convert the fraction directly to a percentage without simplifying first.
-
Convert to a Decimal: Divide the numerator by the denominator:
18 ÷ 60 = 0.3
-
Convert to a Percentage: Multiply the decimal by 100 and add the percentage sign:
0.3 × 100 = 30%
This method yields the same result: 18/60 is 30%. While this method is quicker for simple fractions, simplifying first (as shown in Method 1) is generally recommended for more complex fractions as it reduces the complexity of the decimal calculation.
Understanding the Result: 30%
The result, 30%, signifies that 18 represents 30% of 60. This means if you divide 60 into 100 equal parts, 18 would occupy 30 of those parts. This concept is crucial in many real-world applications, such as calculating sales tax, discounts, and proportions.
Real-World Applications of Percentage Calculations
The ability to convert fractions to percentages is invaluable in numerous situations:
-
Sales and Discounts: Calculating discounts offered on products. For instance, a 30% discount on a $100 item means a saving of $30.
-
Financial Calculations: Determining interest rates, calculating profit margins, and analyzing investment returns.
-
Statistics and Data Analysis: Representing data visually using pie charts and bar graphs, understanding statistical probabilities.
-
Science and Engineering: Expressing experimental results, calculating efficiency and error margins.
-
Everyday Life: Determining tips in restaurants, calculating proportions for recipes, understanding survey results.
Common Misconceptions and Errors
-
Confusing numerator and denominator: Ensure you correctly identify the numerator (the part) and the denominator (the whole) before starting the calculation.
-
Incorrect decimal placement: Pay close attention to decimal points during the division and multiplication steps.
-
Forgetting the percentage sign: Always remember to add the "%" symbol to indicate that the result is a percentage.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to convert fractions to percentages? A: Yes, most calculators have a percentage function that can directly convert fractions to percentages. However, understanding the underlying process is essential for problem-solving and avoiding errors.
-
Q: What if the fraction results in a repeating decimal? A: If the decimal is repeating, you can round it to a certain number of decimal places before converting to a percentage. For instance, 1/3 = 0.333... which can be rounded to 0.33 and then converted to 33%.
-
Q: How do I convert a percentage back to a fraction? A: Divide the percentage by 100 and simplify the resulting fraction. For example, 30% becomes 30/100 which simplifies to 3/10.
Advanced Concepts: Working with Percentages
-
Finding a percentage of a number: To find x% of a number y, multiply y by (x/100). For example, 30% of 50 is 50 * (30/100) = 15.
-
Finding the percentage increase or decrease: To calculate the percentage change, find the difference between the new value and the original value, divide by the original value, and multiply by 100.
-
Working with compound interest: This involves calculating interest not only on the principal amount but also on accumulated interest.
-
Understanding proportional relationships: Percentages are a key tool in understanding and solving proportional problems.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with broad practical applications. Understanding the different methods, as demonstrated with the 18/60 example, allows for efficient and accurate calculations. By mastering this skill, you'll be better equipped to tackle various real-world challenges involving proportions, ratios, and data analysis. Remember to practice regularly and utilize different resources to reinforce your understanding. With consistent effort, you'll develop confidence and proficiency in working with percentages. This detailed explanation and the inclusion of FAQs should provide a solid foundation for your understanding of percentage calculations and their practical uses.
Latest Posts
Latest Posts
-
Fruit Vegetable Beginning With I
Sep 23, 2025
-
Does Standard Deviation Have Units
Sep 23, 2025
-
Time 24 Hour Clock Worksheets
Sep 23, 2025
-
5 Letter Words Starting Le
Sep 23, 2025
-
1200 Sq Feet In Meters
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 18 60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.