4 X 3 X 1
candidatos
Sep 24, 2025 · 6 min read
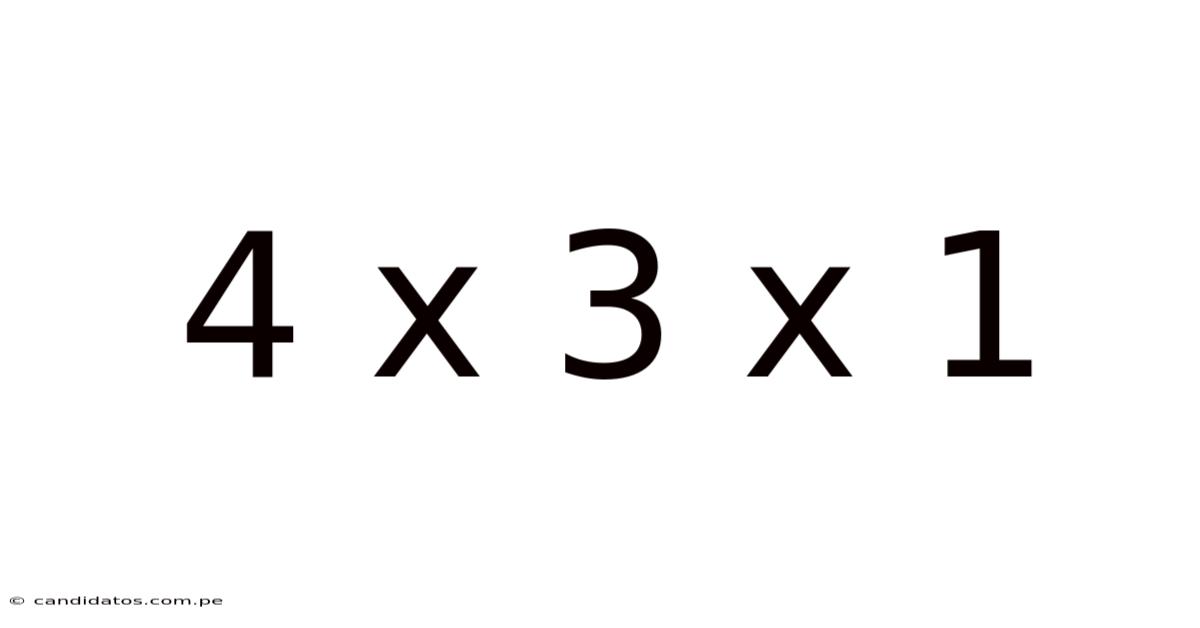
Table of Contents
Decoding 4 x 3 x 1: A Deep Dive into Multiplication, Volume, and Beyond
This article explores the seemingly simple mathematical expression "4 x 3 x 1," delving beyond its basic arithmetic solution to uncover its broader applications in geometry, algebra, and even real-world scenarios. We'll examine the fundamental principles of multiplication, explore its geometric representation, and consider its implications in more complex mathematical contexts. Understanding this seemingly simple equation unlocks a gateway to deeper mathematical concepts.
Introduction: The Foundation of Multiplication
At its core, 4 x 3 x 1 represents a multiplication problem. Multiplication is a fundamental arithmetic operation that signifies repeated addition. In this case, we're essentially adding four groups of three, one time. The result, 12, is straightforward. However, the beauty lies in understanding why this operation is important and how it can be extended to more complex scenarios. The numbers themselves (4, 3, and 1) can represent various quantities, and the operation's significance depends heavily on the context.
Visualizing 4 x 3 x 1: A Geometric Perspective
One of the most powerful ways to understand multiplication is through geometry. We can visualize 4 x 3 x 1 as a rectangular prism (or cuboid). Imagine a box:
- 4: Represents the length of the box.
- 3: Represents the width of the box.
- 1: Represents the height of the box.
The result of 4 x 3 x 1 (12) represents the volume of this box. Volume is the amount of three-dimensional space occupied by an object. In this case, the volume is 12 cubic units. This visualization provides a tangible understanding of multiplication's application beyond simple arithmetic. We can extend this concept to understand volume calculations for various shapes and objects.
Exploring Variations: Manipulating the Numbers
Let's consider what happens when we change the order of the numbers or introduce different values:
-
Commutative Property: Multiplication is commutative, meaning the order of the numbers doesn't affect the result. 4 x 3 x 1 = 3 x 4 x 1 = 1 x 3 x 4 = 12. This property is crucial for understanding and simplifying complex mathematical expressions.
-
Associative Property: Multiplication is also associative, meaning we can group the numbers differently without changing the result. (4 x 3) x 1 = 4 x (3 x 1) = 12. This allows for flexibility in solving more complex problems.
-
Changing the Values: If we change the values, the volume changes accordingly. For example:
- 5 x 2 x 1 = 10 cubic units (a shorter, wider box)
- 2 x 2 x 2 = 8 cubic units (a cube)
- 6 x 2 x 0.5 = 6 cubic units (a flatter box)
These variations highlight the dynamic nature of the equation and its ability to represent a wide range of geometric forms.
Beyond Volume: Applications in Other Fields
The concept of 4 x 3 x 1 extends far beyond basic volume calculations. Consider these applications:
-
Combinatorics: In combinatorics (the study of counting), 4 x 3 x 1 can represent the number of ways to arrange items. For instance, if you have 4 shirts, 3 pants, and 1 pair of shoes, there are 4 x 3 x 1 = 12 different outfits you can create. This illustrates the application of multiplication in scenarios involving choices and permutations.
-
Probability: In probability, multiplication is used to calculate the probability of multiple independent events occurring. If the probability of event A is 4/10, event B is 3/10, and event C is 1/10, the probability of all three events occurring is (4/10) x (3/10) x (1/10) = 12/1000.
-
Algebra: The expression can be generalized to variables. Instead of 4, 3, and 1, we might have 'x', 'y', and 'z', representing unknown quantities. The expression 'xyz' represents the product of three variables, a fundamental concept in algebra. This allows for the representation of relationships between variables and the development of algebraic equations.
The Significance of '1': The Identity Element
The number 1 plays a special role in multiplication. It's the multiplicative identity, meaning that any number multiplied by 1 remains unchanged. In our example, 4 x 3 x 1 = 4 x 3 = 12. The presence of '1' doesn't alter the result but can represent a crucial element in a wider context. For example, it might represent a single unit of measurement, a single option, or a probability of 100%.
Expanding the Scope: Higher Dimensions and Beyond
The concept of volume extends to higher dimensions. While 4 x 3 x 1 represents a three-dimensional volume, we can extrapolate this to represent four-dimensional hypervolumes and beyond using similar principles of multiplication. These higher-dimensional concepts are important in advanced mathematics and physics, particularly in areas such as string theory and tensor calculus. The core principle of repeated multiplication remains consistent even in these abstract mathematical spaces.
Practical Applications: Real-World Examples
Let's look at a few real-world examples to solidify our understanding:
-
Packaging: Imagine a manufacturer designing a box for a product. The dimensions of the box (length, width, height) would be crucial in calculating the volume of the box and determining the amount of material required for packaging. Understanding 4 x 3 x 1 allows for efficient design and material optimization.
-
Construction: In construction, calculating the volume of materials such as concrete or soil is critical for accurate estimation and efficient project planning. Understanding volume calculations is fundamental to accurate budgeting and resource management.
-
Inventory Management: Calculating the storage space required for products in a warehouse involves understanding volume calculations. Efficient storage management requires accurate calculations to optimize space usage and minimize waste.
Addressing Frequently Asked Questions (FAQ)
-
Q: What if one of the numbers is zero? A: If any of the numbers is zero, the result of the multiplication will always be zero (e.g., 4 x 3 x 0 = 0). This is because multiplying by zero results in annihilation of the product.
-
Q: What if one of the numbers is a fraction or decimal? A: The same principles apply. For example, 4 x 3 x 0.5 = 6. The result represents the volume of a flatter box.
-
Q: Can negative numbers be used? A: Yes, negative numbers can be used. The rules of multiplication with negative numbers apply (e.g., a negative number multiplied by a positive number results in a negative number).
-
Q: How does this relate to exponents? A: Exponents represent repeated multiplication of the same number. For instance, 2³ (2 cubed) means 2 x 2 x 2 = 8. While not directly present in 4 x 3 x 1, the concept of repeated multiplication is fundamental to both.
Conclusion: The Power of Simple Multiplication
The seemingly simple expression 4 x 3 x 1 opens a door to a world of mathematical concepts, from basic arithmetic to advanced geometric and algebraic principles. Its application extends far beyond a simple calculation, illuminating the power of multiplication in various fields, from everyday tasks to complex scientific calculations. By understanding the fundamental principles and visualizing the concepts geometrically, we can appreciate the broad reach and practical importance of this fundamental mathematical operation. It’s a reminder that even seemingly simple equations hold within them the potential for profound understanding and application. The beauty lies not just in the answer (12), but in the journey of understanding its implications and applications.
Latest Posts
Latest Posts
-
Musical Instruments Starting With E
Sep 24, 2025
-
Why Does Magnesium Oil Sting
Sep 24, 2025
-
Factor X 2 2x 2
Sep 24, 2025
-
Chemistry Unit 1 And 2
Sep 24, 2025
-
Sodium Hydroxide And Nitric Acid
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 4 X 3 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.