Factor X 2 2x 2
candidatos
Sep 24, 2025 · 6 min read
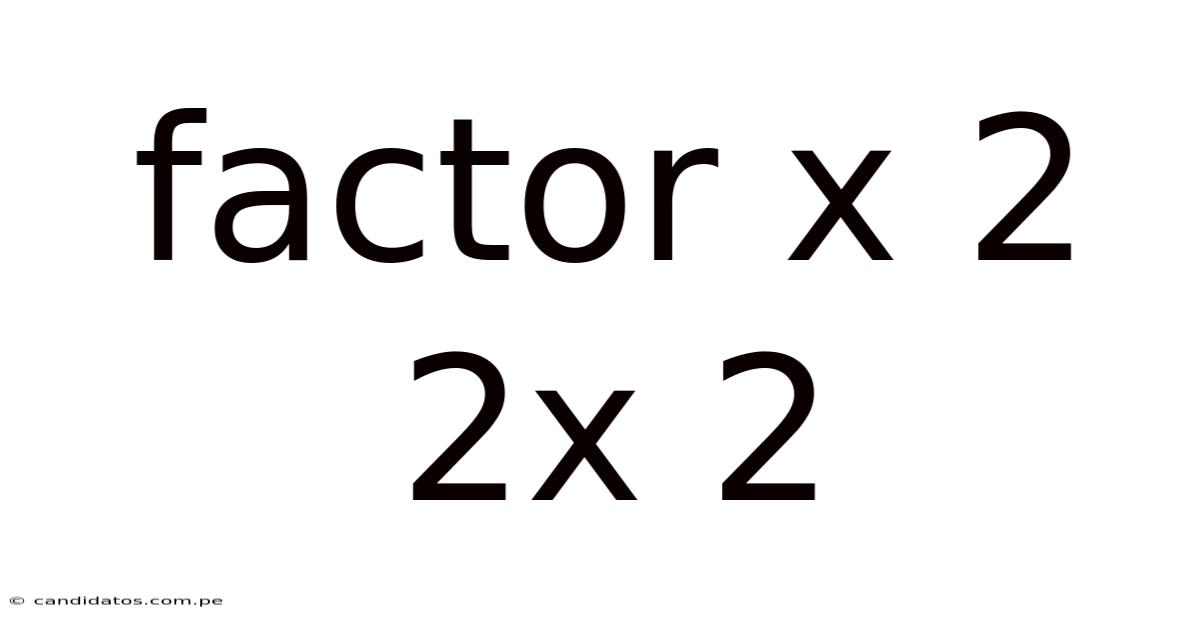
Table of Contents
Decoding the Mystery: A Deep Dive into the Factorization of x² + 2x + 2
The seemingly simple quadratic expression, x² + 2x + 2, often presents a challenge to students learning about factorization. Unlike many quadratics, this one doesn't readily factor using integer coefficients. This article will explore this expression in detail, examining its properties, explaining why it's unfactorable over the integers, demonstrating how to solve for its roots using the quadratic formula, and finally, delving into more advanced techniques for handling such expressions. We will also touch upon its graphical representation and its applications in various mathematical contexts.
Understanding Quadratic Expressions and Factorization
Before diving into the specifics of x² + 2x + 2, let's refresh our understanding of quadratic expressions and factorization. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (typically 'x') is 2. It takes the general form ax² + bx + c, where a, b, and c are constants (numbers).
Factorization, in this context, means expressing the quadratic expression as a product of two linear expressions. For example, the quadratic x² + 5x + 6 can be factored as (x + 2)(x + 3). This is because when you expand (x + 2)(x + 3), you get x² + 5x + 6. This factorization simplifies calculations and is crucial in solving quadratic equations and other mathematical problems.
Why x² + 2x + 2 is Unfactorable Over the Integers
The key to understanding why x² + 2x + 2 doesn't factor nicely lies in the discriminant. The discriminant, denoted as Δ (delta), is the part of the quadratic formula under the square root: b² - 4ac. For our expression, a = 1, b = 2, and c = 2.
Therefore, the discriminant is: Δ = 2² - 4(1)(2) = 4 - 8 = -4.
The significance of the discriminant is this:
- If Δ > 0: The quadratic has two distinct real roots, and it can be factored into two linear expressions with real coefficients.
- If Δ = 0: The quadratic has one repeated real root, and it can be factored as a perfect square.
- If Δ < 0: The quadratic has two complex conjugate roots, and it cannot be factored into two linear expressions with real coefficients (integers included).
Since the discriminant of x² + 2x + 2 is -4, which is less than 0, it confirms that this quadratic cannot be factored using real numbers, let alone integers. This means we cannot find two integers that add up to 2 (the coefficient of x) and multiply to 2 (the constant term).
Finding the Roots Using the Quadratic Formula
Although we cannot factor x² + 2x + 2 using integers, we can still find its roots using the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values (a = 1, b = 2, c = 2), we get:
x = [-2 ± √(-4)] / 2
Since the square root of -4 is 2i (where 'i' is the imaginary unit, √-1), the roots are:
x = (-2 + 2i) / 2 = -1 + i x = (-2 - 2i) / 2 = -1 - i
These are complex conjugate roots. This further reinforces the fact that the quadratic cannot be factored using only real numbers.
Advanced Techniques: Complex Factorization
While factorization over real numbers is impossible, we can express x² + 2x + 2 in factored form using complex numbers:
x² + 2x + 2 = (x - (-1 + i))(x - (-1 - i))
This factorization utilizes the roots we found using the quadratic formula. Although not as straightforward as integer factorization, it is a valid factorization within the complex number system. This form is often valuable in more advanced mathematical contexts.
Graphical Representation
The graph of y = x² + 2x + 2 is a parabola that opens upwards (since the coefficient of x² is positive). Because the discriminant is negative, the parabola does not intersect the x-axis. This visually confirms that there are no real roots. The vertex of the parabola can be found using the formula x = -b/2a = -2/2(1) = -1. Substituting x = -1 into the equation gives y = (-1)² + 2(-1) + 2 = 1. Therefore, the vertex of the parabola is at (-1, 1).
Applications in Mathematics and Beyond
While this particular quadratic may seem abstract, understanding its properties and how to handle it is crucial for several mathematical applications:
- Complex Analysis: The complex roots of this quadratic are essential in understanding complex numbers and their applications in various fields like electrical engineering and quantum mechanics.
- Differential Equations: Quadratics like this frequently appear when solving differential equations, which model numerous real-world phenomena.
- Linear Algebra: The quadratic is related to the characteristic polynomial of a 2x2 matrix, which is crucial in eigenvalue problems in linear algebra.
- Calculus: This quadratic may appear as a part of integrands or in Taylor series expansions of functions.
The inability to factor this quadratic over real numbers highlights the importance of expanding our mathematical toolkit to include complex numbers.
Frequently Asked Questions (FAQ)
Q1: Can I use any other method to solve for the roots besides the quadratic formula?
A1: While completing the square is another valid method for solving quadratic equations, it will lead to the same complex roots in this case. Numerical methods (such as the Newton-Raphson method) could also be used to approximate the roots, but they won't provide the exact complex solutions.
Q2: Is it possible to factor this quadratic using irrational numbers?
A2: No. While the quadratic formula involves a square root, in this case, it results in a complex number (involving 'i'), not an irrational number. Irrational numbers are real numbers that cannot be expressed as a simple fraction, but they are still part of the real number system, unlike complex numbers.
Q3: What is the significance of the complex conjugate roots?
A3: The fact that the roots are complex conjugates (-1 + i and -1 - i) is a general property of quadratic equations with real coefficients and a negative discriminant. Complex roots always come in conjugate pairs. This has important implications in various mathematical and engineering applications.
Q4: Why is factorization important?
A4: Factorization is a powerful tool because it simplifies expressions, making them easier to manipulate and solve. It's crucial for solving equations, simplifying fractions, and understanding the behavior of functions.
Q5: Can I approximate the roots graphically?
A5: You can visually confirm that the parabola doesn't intersect the x-axis, indicating that there are no real roots. However, you cannot accurately determine the complex roots graphically.
Conclusion
While x² + 2x + 2 cannot be factored over the integers or real numbers, understanding why it cannot be factored is as important as understanding how to find its roots. This exploration has highlighted the significance of the discriminant, the power of the quadratic formula in handling even seemingly intractable quadratics, and the crucial role of complex numbers in expanding the scope of our mathematical understanding. The seemingly simple expression x² + 2x + 2 provides a rich learning opportunity, bridging the gap between elementary algebra and more advanced mathematical concepts. Mastering the concepts discussed here lays a strong foundation for tackling more complex problems in various mathematical fields and their applications.
Latest Posts
Latest Posts
-
Lewis Structure For Xenon Tetrafluoride
Sep 24, 2025
-
184 Cm Is How Tall
Sep 24, 2025
-
Km Squared To Miles Squared
Sep 24, 2025
-
100 Meters Is How Far
Sep 24, 2025
-
Poems Written By Rabindranath Tagore
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.