35 40 As A Percentage
candidatos
Sep 22, 2025 · 5 min read
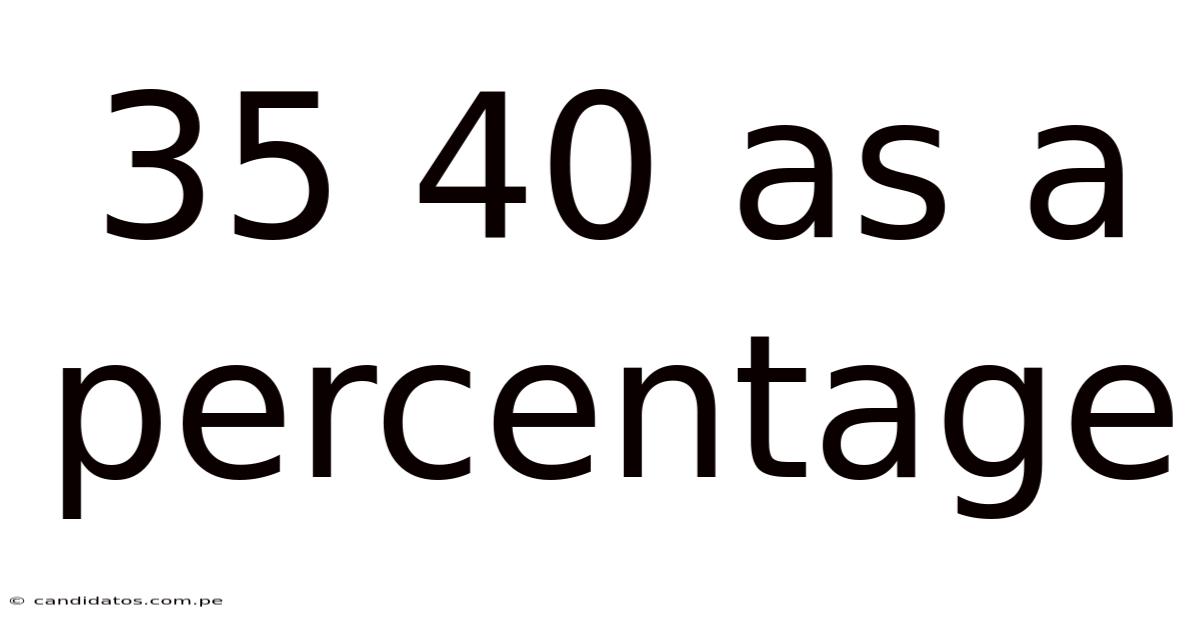
Table of Contents
35/40 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to interpreting statistics and analyzing data. This article will delve into the calculation of 35 out of 40 as a percentage, explaining the process in detail, providing alternative methods, and exploring related concepts. We will also address common questions and misconceptions surrounding percentage calculations. Learning this will equip you with valuable skills for various academic and professional contexts.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. It represents a portion of a whole. The symbol "%" is used to denote a percentage. For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5. Percentages are frequently used to express proportions, rates, and changes.
Calculating 35/40 as a Percentage: The Standard Method
The most straightforward way to calculate 35 out of 40 as a percentage involves converting the fraction to a decimal and then multiplying by 100.
1. Express as a Fraction:
The first step is to represent 35 out of 40 as a fraction: 35/40.
2. Convert to a Decimal:
To convert the fraction to a decimal, divide the numerator (35) by the denominator (40):
35 ÷ 40 = 0.875
3. Multiply by 100:
Finally, multiply the decimal by 100 to express it as a percentage:
0.875 x 100 = 87.5%
Therefore, 35 out of 40 is equal to 87.5%.
Alternative Methods: Simplifying the Fraction
While the standard method is efficient, simplifying the fraction before converting to a decimal can sometimes make the calculation easier.
1. Simplify the Fraction:
The fraction 35/40 can be simplified by finding the greatest common divisor (GCD) of 35 and 40. The GCD of 35 and 40 is 5. Dividing both the numerator and the denominator by 5 gives:
35 ÷ 5 = 7 40 ÷ 5 = 8
This simplifies the fraction to 7/8.
2. Convert to a Decimal:
Now, divide the simplified numerator (7) by the simplified denominator (8):
7 ÷ 8 = 0.875
3. Multiply by 100:
Multiply the decimal by 100 to obtain the percentage:
0.875 x 100 = 87.5%
This method yields the same result: 87.5%. Simplifying the fraction can be particularly helpful when dealing with larger numbers.
Using Proportions: Another Approach
Another way to solve this problem is by using proportions. We can set up a proportion to find the percentage:
35/40 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we can cross-multiply:
40x = 3500
Then, divide both sides by 40:
x = 3500 ÷ 40 = 87.5
Therefore, x = 87.5%. This method demonstrates the fundamental relationship between fractions and percentages.
Interpreting the Result: What Does 87.5% Mean?
The result, 87.5%, signifies that 35 represents 87.5% of 40. This indicates a high proportion – almost 88% – suggesting a strong performance or a significant portion of the total. The context in which this calculation is used will determine the specific interpretation. For instance, if it represents a test score, it signifies a very good result.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Some examples include:
- Academic Performance: Calculating grades, test scores, and overall academic progress.
- Financial Calculations: Determining discounts, interest rates, taxes, profits, and losses.
- Data Analysis: Interpreting statistics, market research, and scientific data.
- Everyday Life: Calculating tips, comparing prices, understanding sales, and more.
Common Mistakes and Misconceptions
Several common mistakes can occur when calculating percentages:
- Incorrect Order of Operations: Always perform division before multiplication when converting a fraction to a percentage.
- Decimal Point Errors: Ensure accurate placement of the decimal point when converting decimals to percentages and vice versa.
- Misunderstanding the Concept: Clearly understand what the percentage represents in the given context.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage increase or decrease?
To calculate a percentage increase or decrease, you need to determine the difference between the two values, divide that difference by the original value, and then multiply by 100.
Q2: What if I need to calculate a percentage of a percentage?
To calculate a percentage of a percentage, simply multiply the two percentages together (after converting them to decimals). For instance, 10% of 20% is calculated as (0.10) x (0.20) = 0.02 or 2%.
Q3: How can I check my percentage calculations?
You can check your calculations by using an online percentage calculator or by working backward from your result to see if it matches the original values.
Advanced Concepts: Percentage Change and Applications
Understanding percentage change is crucial for analyzing trends and making comparisons over time. Percentage change is calculated as:
[(New Value - Old Value) / Old Value] x 100
A positive result indicates an increase, while a negative result signifies a decrease. This formula is vital in various fields, including finance, economics, and science, to understand growth rates, price fluctuations, and other dynamic data.
Furthermore, percentage calculations are essential in statistical analysis, particularly when dealing with probabilities, sampling, and hypothesis testing. For example, confidence intervals are expressed as percentages to indicate the reliability of statistical inferences.
Conclusion
Calculating 35 out of 40 as a percentage, which is 87.5%, is a simple yet fundamental skill. Mastering this process opens the door to understanding and applying percentages in numerous real-world contexts. By understanding the different methods, avoiding common mistakes, and exploring related concepts, you can confidently tackle various percentage-related problems and enhance your analytical skills. The ability to work with percentages is a powerful tool that enhances your critical thinking and problem-solving abilities across many areas of life and work. Remember to practice regularly to build your proficiency and confidence in this essential mathematical skill.
Latest Posts
Latest Posts
-
How To Make A Chatterbox
Sep 22, 2025
-
18 Cm Converted To Inches
Sep 22, 2025
-
Word That Has 12 Letters
Sep 22, 2025
-
1 16 As A Percentage
Sep 22, 2025
-
Difference Between River And Creek
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 35 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.