13 Squared - 12 Squared
candidatos
Sep 16, 2025 · 5 min read
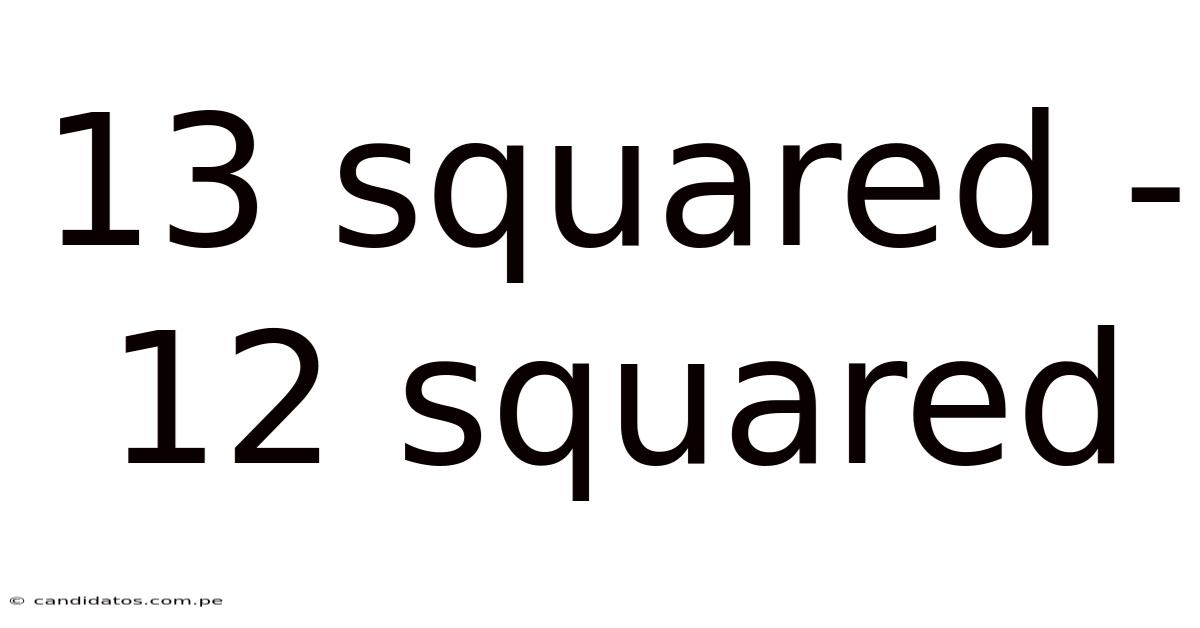
Table of Contents
Unveiling the Mystery: 13 Squared Minus 12 Squared – A Deep Dive into Number Theory
This article explores the seemingly simple mathematical expression "13 squared minus 12 squared" (13² - 12²), delving far beyond the immediate answer to uncover fascinating underlying principles of number theory, algebra, and their practical applications. We'll dissect the problem using multiple approaches, revealing its elegance and connecting it to broader mathematical concepts. Understanding this seemingly basic calculation can open doors to a deeper appreciation of mathematics and its power.
Understanding Squares and the Problem
Before diving into the solution, let's clarify the basics. A square of a number is simply that number multiplied by itself. For instance, 13 squared (13²) is 13 x 13 = 169, and 12 squared (12²) is 12 x 12 = 144. Therefore, the expression 13² - 12² translates to 169 - 144, which directly equals 25. This is the straightforward arithmetic solution. However, the true beauty lies in exploring alternative methods and understanding the underlying mathematical principles.
Method 1: Direct Calculation (The Basic Approach)
The most straightforward method, as mentioned above, is direct calculation:
- Calculate 13²: 13 x 13 = 169
- Calculate 12²: 12 x 12 = 144
- Subtract 12² from 13²: 169 - 144 = 25
This method is simple and effective for small numbers, but it becomes less efficient as the numbers grow larger. It doesn't illuminate the underlying mathematical structure.
Method 2: Difference of Squares – Unveiling the Algebraic Elegance
This problem showcases a fundamental algebraic identity: the difference of squares. This identity states that for any two numbers, a and b:
a² - b² = (a + b)(a - b)
Applying this to our problem (where a = 13 and b = 12):
13² - 12² = (13 + 12)(13 - 12) = (25)(1) = 25
This method is significantly more efficient and reveals a crucial algebraic concept. It highlights the factorization of the difference of squares, transforming a subtraction problem into a multiplication problem. This approach is far more powerful and scalable than direct calculation.
Method 3: Visual Representation – Geometry to the Rescue
The difference of squares can also be visualized geometrically. Imagine a large square with sides of length 13 units. Now, imagine a smaller square within it, with sides of length 12 units. The area of the larger square is 13² (169 square units), and the area of the smaller square is 12² (144 square units). The difference between these areas represents the area of the remaining region, which is a border surrounding the smaller square.
This border can be divided into three rectangles: two with dimensions 12 x 1 and one with dimensions 1 x 1. The total area of the border is (12 x 1) + (12 x 1) + (1 x 1) = 25 square units. This geometric representation provides an intuitive understanding of the difference of squares, demonstrating the connection between algebra and geometry.
Method 4: The Pattern and its Implications
Let's consider a series of similar calculations:
- 2² - 1² = 3
- 3² - 2² = 5
- 4² - 3² = 7
- 5² - 4² = 9
- 6² - 5² = 11
- and so on...
Notice a pattern? The results are consecutive odd numbers. This is not a coincidence. The difference of squares of two consecutive integers always results in an odd number. This observation stems directly from the algebraic identity (a + b)(a - b) where, when a and b are consecutive integers, (a-b) always equals 1. Therefore, the result is always a + b, which will always be odd if a and b are consecutive integers (one even, one odd).
Beyond the Numbers: Applications and Extensions
The difference of squares is not just a mathematical curiosity; it has numerous applications in various fields:
- Algebraic Manipulation: It's a crucial tool for simplifying algebraic expressions and solving equations.
- Calculus: The concept underlies differentiation and integration techniques.
- Physics: It appears in various physics formulas, particularly in problems involving energy and motion.
- Computer Science: Efficient algorithms often utilize the properties of the difference of squares for optimized calculations.
Furthermore, we can extend this concept to non-consecutive integers. For example, let's consider 15² - 5²:
15² - 5² = (15 + 5)(15 - 5) = (20)(10) = 200
The difference of squares provides a powerful and elegant way to solve such problems efficiently.
Frequently Asked Questions (FAQs)
Q: Is there a limit to the size of numbers for which the difference of squares formula works?
A: No, the difference of squares formula (a² - b² = (a + b)(a - b)) works for any real numbers a and b, regardless of their size or whether they are integers or decimals.
Q: Can the difference of squares be used with cubes or higher powers?
A: While there isn't a direct equivalent for cubes (a³ - b³), there are factorization formulas for the difference of cubes and higher powers. These are more complex but serve a similar purpose of simplifying calculations.
Q: What is the significance of the pattern of consecutive odd numbers we observed?
A: The pattern of consecutive odd numbers highlights the relationship between the difference of squares and the sum of consecutive odd numbers. This connection reveals a deeper structure within number theory and provides alternative methods for calculating sums of odd numbers.
Conclusion: More Than Just a Calculation
The seemingly simple problem of 13² - 12² serves as a gateway to understanding fundamental concepts in algebra and number theory. By exploring different solution methods, we've unveiled the elegant difference of squares formula, its geometric interpretation, and its broader applications. This journey highlights the power of mathematics, demonstrating how seemingly basic calculations can unveil profound principles and practical tools relevant across diverse fields. The key takeaway isn't just the answer (25), but the underlying mathematical elegance and its far-reaching implications. This exploration encourages a deeper appreciation for the interconnectedness and beauty of mathematics. It’s not just about numbers; it's about understanding the patterns, the relationships, and the power of mathematical reasoning.
Latest Posts
Latest Posts
-
Number Line From 1 10
Sep 16, 2025
-
Volume Of Cylinder In Litres
Sep 16, 2025
-
15 Percent As A Fraction
Sep 16, 2025
-
Another Term For Quick Learner
Sep 16, 2025
-
How Animals Eat Their Food
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 13 Squared - 12 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.