3 4 Multiplied By 2
candidatos
Sep 21, 2025 · 6 min read
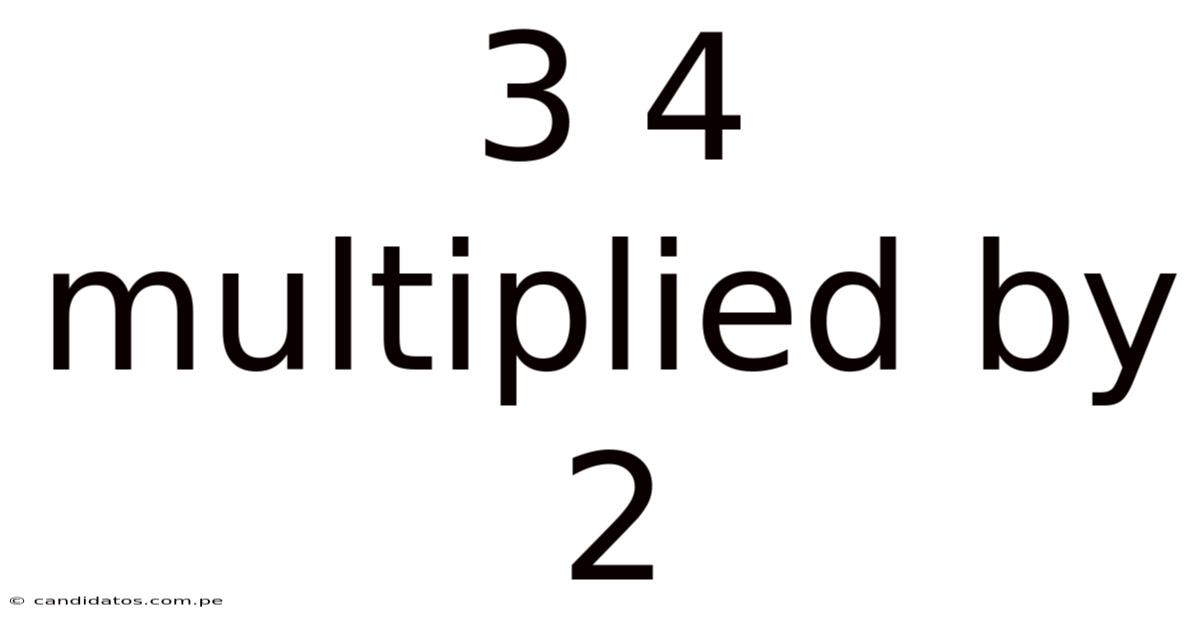
Table of Contents
Decoding 3/4 Multiplied by 2: A Deep Dive into Fractions and Multiplication
This article explores the seemingly simple mathematical problem of 3/4 multiplied by 2, delving far beyond just the answer. We'll uncover the underlying principles of fraction multiplication, explore multiple methods of solving the problem, and examine the real-world applications of this fundamental concept. Understanding this seemingly simple calculation unlocks a deeper understanding of fractions and their role in various mathematical operations. This comprehensive guide is designed for learners of all levels, from those just grasping the basics of fractions to those seeking a more nuanced understanding of mathematical operations.
Understanding Fractions: A Quick Recap
Before tackling the multiplication, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the denominator (4) signifies that the whole is divided into four equal parts, and the numerator (3) indicates that we are considering three of those parts.
Method 1: Direct Multiplication
The most straightforward approach to solving 3/4 multiplied by 2 is through direct multiplication. We multiply the numerator of the fraction by the whole number:
3/4 * 2 = (3 * 2) / 4 = 6/4
This result, 6/4, is an improper fraction because the numerator (6) is larger than the denominator (4). Improper fractions are perfectly valid, but they are often simplified into mixed numbers.
Converting to Mixed Numbers
A mixed number combines a whole number and a proper fraction. To convert 6/4 to a mixed number, we divide the numerator (6) by the denominator (4):
6 ÷ 4 = 1 with a remainder of 2
This means that 6/4 contains one whole unit and a remaining 2/4. Therefore, 6/4 is equivalent to 1 2/4.
Simplifying Fractions
The fraction 2/4 can be further simplified. Both the numerator and the denominator are divisible by 2:
2/4 = (2 ÷ 2) / (4 ÷ 2) = 1/2
Therefore, the simplified mixed number is 1 1/2. This is our final answer using the direct multiplication method.
Method 2: Converting to a Decimal
Another approach involves converting the fraction 3/4 to its decimal equivalent before performing the multiplication. To convert a fraction to a decimal, we divide the numerator by the denominator:
3 ÷ 4 = 0.75
Now, we multiply the decimal equivalent by 2:
0.75 * 2 = 1.5
Notice that 1.5 is the decimal equivalent of 1 1/2, confirming our previous result. This method demonstrates the interchangeability between fractions and decimals.
Method 3: Visual Representation
For a more intuitive understanding, let's visualize the problem. Imagine a pizza cut into four equal slices. 3/4 represents three slices of the pizza. Multiplying by 2 means we have two such sets of three slices:
- Set 1: 3/4 of the pizza (three slices)
- Set 2: 3/4 of the pizza (three slices)
In total, we have six slices (6/4 or 1 1/2 pizzas). This visual approach reinforces the concept of multiplication as repeated addition.
The Importance of Fraction Multiplication in Real Life
Understanding fraction multiplication is crucial for tackling numerous real-world problems. Consider these examples:
- Cooking: A recipe calls for 3/4 cup of flour, and you need to double the recipe. Fraction multiplication helps determine the total amount of flour required (3/4 * 2 = 1 1/2 cups).
- Construction: Measuring materials for building projects often involves fractions. Calculating the length of a beam or the area of a surface requires understanding fraction multiplication.
- Finance: Calculating percentages, interest rates, and discounts all rely on the principles of fraction multiplication.
- Science: Many scientific measurements involve fractions, particularly when dealing with smaller units. Analyzing data and performing experiments often requires the manipulation of fractional values.
Expanding on the Concepts: Exploring More Complex Fractions
While 3/4 multiplied by 2 is a relatively simple problem, it lays the groundwork for understanding more complex fraction multiplications. Let's consider a scenario involving multiplying two fractions:
1/2 * 3/4
To multiply fractions, we simply multiply the numerators together and the denominators together:
(1 * 3) / (2 * 4) = 3/8
This simple operation highlights the fundamental rules of fraction multiplication. Understanding this concept is crucial for solving more complex equations involving fractions and other mathematical operations.
Addressing Potential Misconceptions
A common misconception in fraction multiplication is incorrectly adding the numerators and denominators. Remember, we multiply the numerators and multiply the denominators, not add them. This distinction is critical for accurately calculating the result. Another potential area of confusion is simplifying fractions. Always simplify your answer to its lowest terms to obtain the most accurate and concise result.
Frequently Asked Questions (FAQ)
Q: Can I multiply a fraction by a whole number in any order?
A: Yes, multiplication is commutative, meaning the order of the numbers doesn't affect the result. 3/4 * 2 is the same as 2 * 3/4.
Q: What if the whole number is a decimal?
A: You can still use the same method. Convert the decimal to a fraction (if necessary) and multiply the numerators and denominators as before. Or, you can multiply the fraction's decimal equivalent by the decimal number.
Q: How do I multiply mixed numbers?
A: First, convert the mixed numbers into improper fractions. Then, multiply the numerators and denominators as you would with any other fractions. Finally, simplify the result and convert it back to a mixed number if necessary.
Q: What if I get a fraction with a very large numerator and denominator?
A: Simplify the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD.
Conclusion: Mastering Fraction Multiplication
Mastering the multiplication of fractions, even seemingly simple problems like 3/4 multiplied by 2, forms a crucial foundation for more advanced mathematical concepts. Understanding the underlying principles, exploring different solution methods, and visualizing the process all contribute to a more comprehensive grasp of this vital mathematical operation. By applying these techniques and understanding the real-world applications, you'll be well-equipped to tackle more complex problems and confidently navigate the world of fractions and numbers. Remember, consistent practice and a deep understanding of the fundamentals are key to success in mathematics. The journey to mastering fractions is a rewarding one, opening doors to a wider understanding of the mathematical world and its relevance to everyday life.
Latest Posts
Latest Posts
-
Words That Rhyme With Ball
Sep 21, 2025
-
The Best Couch Potato List
Sep 21, 2025
-
Format For Letter Of Authorization
Sep 21, 2025
-
Blue Colour Fruits And Vegetables
Sep 21, 2025
-
Sin X Sin 180 X
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Multiplied By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.