Sin X Sin 180 X
candidatos
Sep 21, 2025 · 6 min read
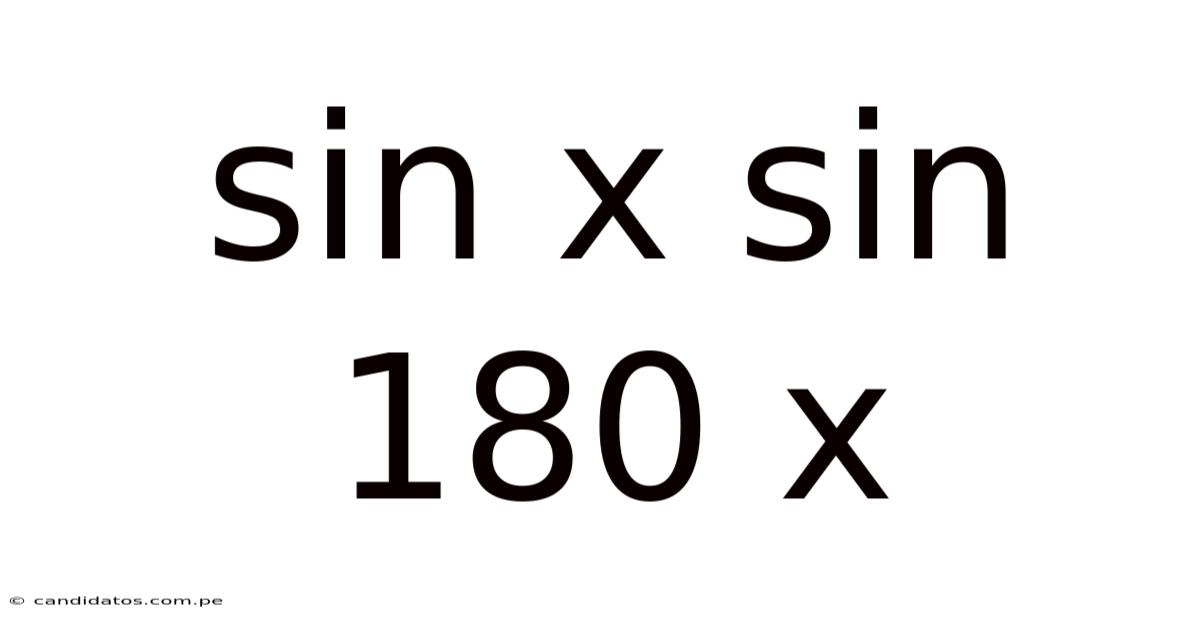
Table of Contents
Unraveling the Mystery: sin x sin 180° - x
Understanding trigonometric identities is crucial for anyone delving into mathematics, physics, or engineering. This article dives deep into the intriguing relationship between sin x and sin (180° - x), exploring its proof, applications, and significance in various mathematical contexts. We'll uncover why this identity holds true and how it can simplify complex calculations, making it a valuable tool in your mathematical arsenal.
Introduction
The expression sin x sin (180° - x) represents a fundamental trigonometric identity. This identity, often overlooked in its simplicity, provides a powerful shortcut in solving numerous trigonometric problems. It's based on the properties of angles and their relationship within the unit circle, allowing us to manipulate and simplify equations involving sine functions. This article will not only prove this identity but also demonstrate its practical applications and explore its connection to other trigonometric concepts. Mastering this identity enhances your understanding of trigonometric functions and expands your problem-solving capabilities.
Understanding the Unit Circle
Before we delve into the proof, it's essential to refresh our understanding of the unit circle. The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. Any point on the unit circle can be represented by its coordinates (cos θ, sin θ), where θ is the angle formed between the positive x-axis and the line segment connecting the origin to that point.
This geometric representation is vital because it visually demonstrates the relationship between angles and their trigonometric functions. Angles are measured counterclockwise from the positive x-axis. Understanding this visual representation will greatly assist in grasping the proof and application of the sin x sin (180° - x) identity.
Proving the Identity: sin x sin (180° - x) = sin²x
There are several ways to prove this identity. We'll explore two common approaches: using the sine subtraction formula and using the unit circle's properties.
Method 1: Using the Sine Subtraction Formula
The sine subtraction formula states that sin (A - B) = sin A cos B - cos A sin B. Let's apply this formula to our expression:
sin (180° - x) = sin 180° cos x - cos 180° sin x
Since sin 180° = 0 and cos 180° = -1, the equation simplifies to:
sin (180° - x) = 0 * cos x - (-1) * sin x = sin x
Therefore, sin x sin (180° - x) becomes sin x * sin x, which simplifies to sin²x.
Method 2: Geometric Proof Using the Unit Circle
Consider an angle x in the first quadrant of the unit circle. The y-coordinate of the point on the unit circle corresponding to angle x is sin x. Now consider the angle (180° - x). This angle lies in the second quadrant. Notice that the y-coordinate of the point corresponding to (180° - x) is also sin x. This is because the sine function represents the y-coordinate on the unit circle, and the y-coordinate for angle x and (180° -x) have the same magnitude. Since both angles share the same y-coordinate (which is sin x), we can deduce that sin x = sin (180° - x). Consequently, sin x sin (180° - x) = sin x * sin x = sin²x.
Applications of the Identity
The identity sin x sin (180° - x) = sin²x has several significant applications in various mathematical fields. Some prominent examples include:
-
Simplifying Trigonometric Equations: This identity simplifies complex trigonometric expressions, making them easier to solve. For example, an equation involving sin x sin (180° - x) can be readily simplified to an equation involving sin²x, which might be easier to manage.
-
Calculus: In calculus, this identity can be instrumental in simplifying integrals and derivatives involving trigonometric functions. By replacing sin x sin (180° - x) with sin²x, complex integrations can sometimes be simplified using known power-reducing formulas for trigonometric functions.
-
Physics and Engineering: Many applications in physics and engineering involve trigonometric functions, particularly in oscillatory motion, wave phenomena, and AC circuit analysis. This identity proves useful in simplifying these equations, leading to easier problem solving.
-
Geometry: This identity has implications in geometrical problem-solving, particularly in situations involving triangles and circles where angles and their sine values play a significant role.
Extending the Concept: sin x sin (360° - x)
A related but slightly different identity involves the angle (360° - x). Let's explore this:
Using the sine subtraction formula, we have:
sin (360° - x) = sin 360° cos x - cos 360° sin x
Since sin 360° = 0 and cos 360° = 1, this simplifies to:
sin (360° - x) = -sin x
Therefore, sin x sin (360° - x) = sin x (-sin x) = -sin²x
This demonstrates that while the identity for (180° - x) results in a positive value, the identity for (360° - x) yields a negative value. This difference is crucial and highlights the importance of understanding the quadrant where the angle lies within the unit circle.
Frequently Asked Questions (FAQ)
-
Q: Is this identity valid for all values of x?
- A: Yes, the identity sin x sin (180° - x) = sin²x is valid for all real values of x. This is because both sin x and sin (180° - x) are defined for all real numbers.
-
Q: How is this identity different from other trigonometric identities?
- A: While there are many trigonometric identities, this one provides a specific simplification involving the product of sines of supplementary angles. It offers a direct substitution that can greatly streamline calculations.
-
Q: Can this identity be used with radians instead of degrees?
- A: Yes, the identity remains valid when using radians. The equivalent expression would be sin x sin (π - x) = sin²x.
-
Q: What are some common mistakes to avoid when using this identity?
- A: A common mistake is misinterpreting the relationship between x and (180° - x) or (π - x). Ensure you accurately apply the identity to avoid incorrect simplifications. Also, be mindful of the signs in similar identities, such as the one involving (360° - x).
Conclusion
The trigonometric identity sin x sin (180° - x) = sin²x is a powerful tool in simplifying complex mathematical expressions. Its proof, based on the sine subtraction formula or the geometric properties of the unit circle, establishes its validity. Understanding this identity significantly expands your mathematical toolkit, offering practical applications in diverse fields including calculus, physics, engineering, and geometry. By mastering this identity, you not only enhance your problem-solving capabilities but also deepen your understanding of trigonometric relationships within the unit circle. Remember to always consider the quadrant of the angle and be aware of the sign implications, especially when dealing with related identities involving different angles. This comprehensive exploration serves as a solid foundation for further exploration of trigonometric identities and their applications.
Latest Posts
Latest Posts
-
Electronic Components In A Circuit
Sep 21, 2025
-
350 Usd In Indian Rupees
Sep 21, 2025
-
Coarse Focus Knob Microscope Function
Sep 21, 2025
-
Deck Of Cards And Probability
Sep 21, 2025
-
Public And Private Company Difference
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Sin X Sin 180 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.