2 X 3 X 5
candidatos
Sep 21, 2025 · 7 min read
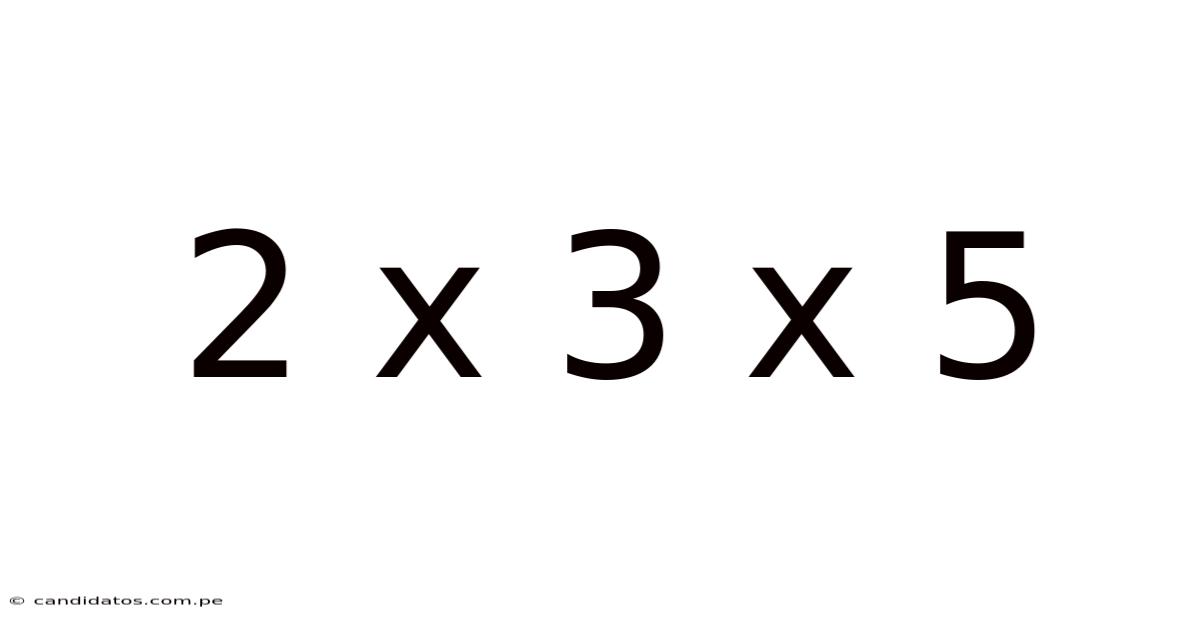
Table of Contents
Unveiling the Secrets of 2 x 3 x 5: A Deep Dive into Prime Factorization and Beyond
This article explores the seemingly simple equation 2 x 3 x 5 = 30, delving far beyond the basic arithmetic. We'll uncover its significance in mathematics, its applications in various fields, and the underlying concepts that make it a cornerstone of number theory. Understanding this seemingly simple calculation opens doors to comprehending more complex mathematical ideas, from prime factorization to the building blocks of larger numbers. This exploration is ideal for anyone looking to strengthen their understanding of fundamental mathematical principles.
Understanding the Fundamentals: Prime Numbers and Factorization
Before diving into the intricacies of 2 x 3 x 5, let's refresh our understanding of some key mathematical concepts.
Prime Numbers: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The numbers 2, 3, and 5 in our equation are all prime numbers. This means they are indivisible by any other whole number except 1 and themselves. Prime numbers are the fundamental building blocks of all other whole numbers.
Prime Factorization: Prime factorization is the process of expressing a composite number (a number that is not prime) as a product of its prime factors. Our equation, 2 x 3 x 5 = 30, showcases the prime factorization of 30. It tells us that 30 can be broken down into the product of these three prime numbers and no others. This representation is unique for every composite number, a fundamental theorem in number theory known as the Fundamental Theorem of Arithmetic.
The Significance of 30: The number 30 itself holds several mathematical and historical interests. It’s the smallest number divisible by 1, 2, 3, 5, 6, 10, and 15. This property makes it a highly composite number – a number with more divisors than any smaller positive integer. In some ancient cultures, 30 held significant calendrical importance.
Exploring the Equation: 2 x 3 x 5 = 30
Now, let's delve deeper into the equation 2 x 3 x 5 = 30. This seemingly simple equation reveals a wealth of mathematical concepts:
-
Multiplication as Repeated Addition: At its most basic level, this equation represents repeated addition. 2 x 3 means adding 2 three times (2 + 2 + 2 = 6), and then multiplying this by 5 signifies adding 6 five times (6 + 6 + 6 + 6 + 6 = 30). This provides a foundation for understanding multiplication's relationship to addition.
-
Commutative Property: The order of the numbers in multiplication doesn't affect the result. We could rearrange the equation as 3 x 5 x 2 = 30, 5 x 2 x 3 = 30, and so on, without changing the final answer. This property is known as the commutative property of multiplication.
-
Associative Property: Similarly, the grouping of numbers doesn't affect the result. We could group the numbers as (2 x 3) x 5 = 30 or 2 x (3 x 5) = 30. This is the associative property of multiplication.
-
Distributive Property: The distributive property links multiplication and addition. For example, we can express 30 as (2 x 3) + (2 x 27) or other combinations that demonstrate the distributive property of multiplication over addition.
Applications in Various Fields
The concept of prime factorization, embodied in the equation 2 x 3 x 5 = 30, has far-reaching applications beyond pure mathematics:
-
Cryptography: Prime numbers form the backbone of modern cryptography. Algorithms like RSA encryption rely on the difficulty of factoring extremely large numbers into their prime components. The security of online transactions and sensitive data hinges on this principle.
-
Computer Science: Understanding prime factorization is crucial in various algorithms related to data structures and number theory applications within computer science. Efficient algorithms for prime factorization are continually being developed and refined.
-
Coding Theory: Prime numbers play a significant role in error-correcting codes used in data transmission and storage. These codes ensure reliable data transfer even in the presence of noise or errors.
-
Music Theory: Interestingly, prime numbers have found applications in music theory. The relationships between intervals in music can sometimes be expressed using prime numbers, leading to insights into harmonic structures and musical compositions.
-
Physics: Prime numbers unexpectedly appear in certain areas of physics, particularly in the study of quantum mechanics and chaotic systems. While the connection isn't fully understood, these appearances suggest a deeper, possibly unforeseen connection between prime numbers and the laws of nature.
Beyond 30: Exploring Larger Numbers and Factorization
The principles demonstrated by 2 x 3 x 5 = 30 extend to larger numbers. Consider the number 60: its prime factorization is 2² x 3 x 5. This shows how larger composite numbers are built from combinations of prime numbers. Finding the prime factorization of larger numbers can be more challenging, but algorithms and techniques exist to efficiently determine them, even for very large numbers. These techniques are fundamental in fields like cryptography, as mentioned earlier.
Practical Applications and Real-World Examples
Let's look at some practical examples where understanding the concepts of prime factorization and the equation 2 x 3 x 5 = 30 prove useful:
-
Divisibility Rules: Knowing that 30 is composed of 2, 3, and 5 allows us to quickly determine its divisibility by these numbers. This extends to understanding divisibility rules for other numbers.
-
Finding Common Factors: When working with fractions, finding the greatest common factor (GCF) is essential for simplification. Knowing the prime factorization of numbers makes finding the GCF much simpler. For example, finding the GCF of 30 and 60 is easily accomplished by analyzing their prime factorizations (2 x 3 x 5 and 2² x 3 x 5).
-
Least Common Multiple: Similarly, finding the least common multiple (LCM) of numbers is crucial in various mathematical operations, particularly when dealing with fractions or working with different time cycles. Understanding prime factorization simplifies this task.
-
Problem Solving: Many mathematical problems, especially in areas like algebra and number theory, benefit significantly from understanding prime factorization and the underlying principles.
Frequently Asked Questions (FAQs)
Q: Is 30 the only number that can be expressed as the product of 2, 3, and 5?
A: Yes, due to the Fundamental Theorem of Arithmetic, 30 has a unique prime factorization. No other combination of prime numbers will yield 30.
Q: How do I find the prime factorization of a larger number?
A: Several methods exist, including trial division (dividing by increasingly larger prime numbers), and more sophisticated algorithms like the Pollard rho algorithm and the general number field sieve, which are used for very large numbers.
Q: What is the importance of prime numbers in cryptography?
A: The difficulty of factoring very large numbers into their prime components forms the basis of many encryption algorithms. The security of online transactions relies on this computational challenge.
Q: Are there any patterns in the distribution of prime numbers?
A: While there's no simple formula to predict prime numbers, their distribution has been studied extensively. The Prime Number Theorem provides an approximation of the number of primes less than a given number, although it doesn't precisely pinpoint individual primes. The distribution remains a topic of ongoing research in number theory.
Conclusion: The Enduring Significance of 2 x 3 x 5 = 30
The seemingly simple equation 2 x 3 x 5 = 30 offers a gateway to understanding profound mathematical concepts. From the fundamentals of prime factorization and the properties of multiplication to its diverse applications in various fields, this equation provides a powerful illustration of the building blocks of mathematics and its influence on our world. Exploring this equation encourages us to appreciate the elegance and power of mathematical principles that underly complex systems and processes, both natural and man-made. The journey from a simple equation to a deeper understanding of number theory is a testament to the enduring power of mathematical exploration. By understanding the foundations, we can unlock the secrets of more complex numerical relationships and applications.
Latest Posts
Latest Posts
-
How To Multiply Algebraic Fractions
Sep 21, 2025
-
Difference Between Center And Centre
Sep 21, 2025
-
5 Million Dollars In Rupees
Sep 21, 2025
-
9 12 As A Percent
Sep 21, 2025
-
Incline Plane Free Body Diagram
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 2 X 3 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.