2 X 2 X 12
candidatos
Sep 17, 2025 · 6 min read
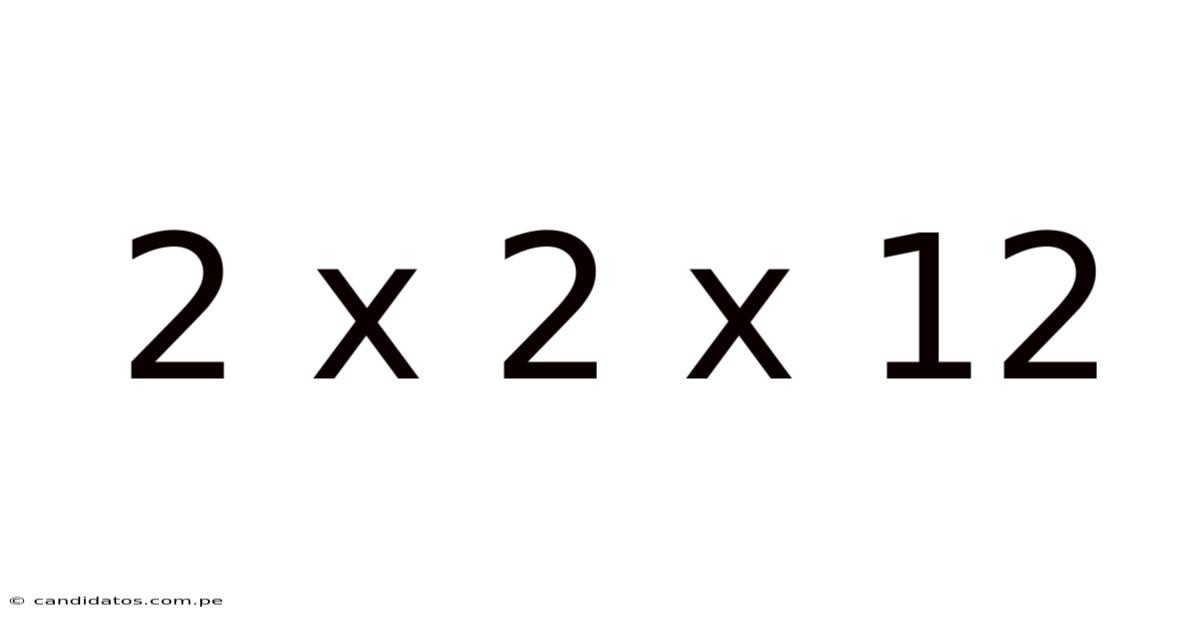
Table of Contents
Exploring the Mathematical Landscape of 2 x 2 x 12: Beyond Simple Multiplication
This article delves into the seemingly simple mathematical expression "2 x 2 x 12," uncovering its multifaceted nature and exploring its applications across various fields. We'll move beyond the basic calculation to examine its implications in geometry, algebra, and even real-world scenarios. Understanding this seemingly basic equation can open doors to a deeper appreciation of mathematical principles and their practical use.
The Fundamentals: Calculating 2 x 2 x 12
At its core, "2 x 2 x 12" is a straightforward multiplication problem. The calculation proceeds as follows:
- 2 x 2 = 4: We begin by multiplying the first two numbers.
- 4 x 12 = 48: Next, we multiply the result by the third number.
Therefore, the solution to 2 x 2 x 12 is 48. This simple calculation forms the basis for exploring more complex concepts.
Geometric Interpretations: Volume and Dimensions
The expression "2 x 2 x 12" readily lends itself to a geometric interpretation. Imagine a rectangular prism (or cuboid). The numbers represent the dimensions of this prism:
- 2: Length
- 2: Width
- 12: Height
The result of the multiplication, 48, represents the volume of this rectangular prism. This means that the prism can hold 48 cubic units of space. This visualization helps to contextualize the abstract mathematical operation, making it more tangible and understandable. This understanding of volume is crucial in fields like architecture, engineering, and even packaging design.
Algebraic Extensions: Variables and Equations
We can extend this concept into the realm of algebra by introducing variables. Let's represent the dimensions as:
- Length (l) = 2
- Width (w) = 2
- Height (h) = 12
The formula for the volume (V) of a rectangular prism is: V = l x w x h
Substituting our values, we get: V = 2 x 2 x 12 = 48.
This simple equation can be modified. For instance, if we know the volume (48) and two dimensions (2 and 2), we can solve for the unknown height:
- 48 = 2 x 2 x h
- 48 = 4h
- h = 48/4 = 12
This demonstrates how the basic multiplication problem can be incorporated into more complex algebraic equations and problem-solving. The ability to manipulate equations and solve for unknowns is a fundamental skill in many scientific and engineering disciplines.
Real-World Applications: From Boxes to Buildings
The concept of 2 x 2 x 12, and its representation of volume, appears in numerous real-world situations:
-
Packaging: Imagine designing a box to hold a specific item. If the item requires a volume of 48 cubic inches, the designer might consider a box with dimensions of 2 x 2 x 12 inches. This is just one possible configuration; other combinations of length, width, and height could also yield a volume of 48 cubic inches. Finding the optimal dimensions often involves considering factors beyond just volume, such as material cost and ease of handling.
-
Construction: In construction, the calculation of volume is critical for estimating the amount of materials needed for a project. For example, calculating the volume of concrete required for a foundation or the volume of fill needed for landscaping would involve similar multiplication calculations. Accurate volume calculations are essential for cost estimation and project planning.
-
Data Storage: In the digital world, data storage is often measured in cubic units (though not literally cubic inches or centimeters, but rather in units like gigabytes or terabytes). While the units differ, the underlying concept of volume and the use of multiplication to determine capacity remain the same. A server's storage space might be described in terms of dimensions analogous to length, width, and height, although these dimensions might represent aspects such as processing power, memory, and disk space.
-
Inventory Management: Warehouses utilize volume calculations extensively to optimize storage and retrieval of goods. Knowing the volume of individual items and the overall warehouse space helps in designing efficient storage layouts, minimizing wasted space, and streamlining logistical operations.
Exploring Variations: Factors and Multiples
The number 48, resulting from 2 x 2 x 12, has several interesting mathematical properties. Let's explore some of these:
-
Factors: The factors of 48 are the numbers that divide evenly into 48. These include 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. Understanding factors is crucial in many mathematical operations, including simplifying fractions and solving equations.
-
Multiples: Multiples of 48 are the numbers obtained by multiplying 48 by any whole number. These include 48, 96, 144, 192, and so on. The concept of multiples is essential in understanding number patterns and sequences.
-
Prime Factorization: The prime factorization of 48 is 2⁴ x 3. This means that 48 can be expressed as the product of its prime factors (numbers divisible only by 1 and themselves). Prime factorization is a fundamental concept in number theory and has applications in cryptography and other advanced mathematical fields.
Beyond the Numbers: Developing Mathematical Thinking
The seemingly simple problem of 2 x 2 x 12 offers a gateway to a deeper understanding of mathematical concepts. It highlights the interconnectedness of arithmetic, geometry, and algebra. The ability to translate a simple multiplication problem into a geometric representation, an algebraic equation, and a real-world application showcases the power of mathematical thinking.
Frequently Asked Questions (FAQ)
-
Q: Are there other ways to obtain a volume of 48 cubic units?
- A: Absolutely! There are many combinations of length, width, and height that would result in a volume of 48 cubic units. For example, 1 x 6 x 8, 3 x 4 x 4, and 1 x 1 x 48 are just a few possibilities. The specific dimensions would depend on the constraints of the particular application.
-
Q: What if one of the dimensions was a decimal?
- A: The same principles apply. If one dimension was, for example, 2.5, the calculation would still be straightforward: 2 x 2.5 x 12 = 60. The resulting volume would simply be 60 cubic units.
-
Q: How does this relate to more advanced mathematical concepts?
- A: The foundation of understanding volume calculations like this is crucial for later work in calculus (calculating volumes of irregular shapes), linear algebra (dealing with multi-dimensional spaces), and other advanced mathematical disciplines.
Conclusion: The Enduring Significance of 2 x 2 x 12
The seemingly simple calculation of 2 x 2 x 12 reveals a wealth of mathematical concepts and applications. From the basic act of multiplication to the visualization of volume, the solving of algebraic equations, and the interpretation in real-world scenarios, this expression demonstrates the power and versatility of mathematics. Understanding this simple problem strengthens the foundation for tackling more complex mathematical challenges and fosters a deeper appreciation for the relevance of mathematics in various aspects of life. It underscores that even the simplest mathematical concepts can hold profound implications and far-reaching applications. The key is to not just calculate the answer, but to understand the underlying principles and explore its connections to broader mathematical and real-world contexts.
Latest Posts
Latest Posts
-
1500 Sq Feet To Meters
Sep 17, 2025
-
11 20 As A Percent
Sep 17, 2025
-
What Is Interconnection In Geography
Sep 17, 2025
-
Advantages Of Human Development Index
Sep 17, 2025
-
26 36 As A Percentage
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.