11 20 As A Percent
candidatos
Sep 17, 2025 · 6 min read
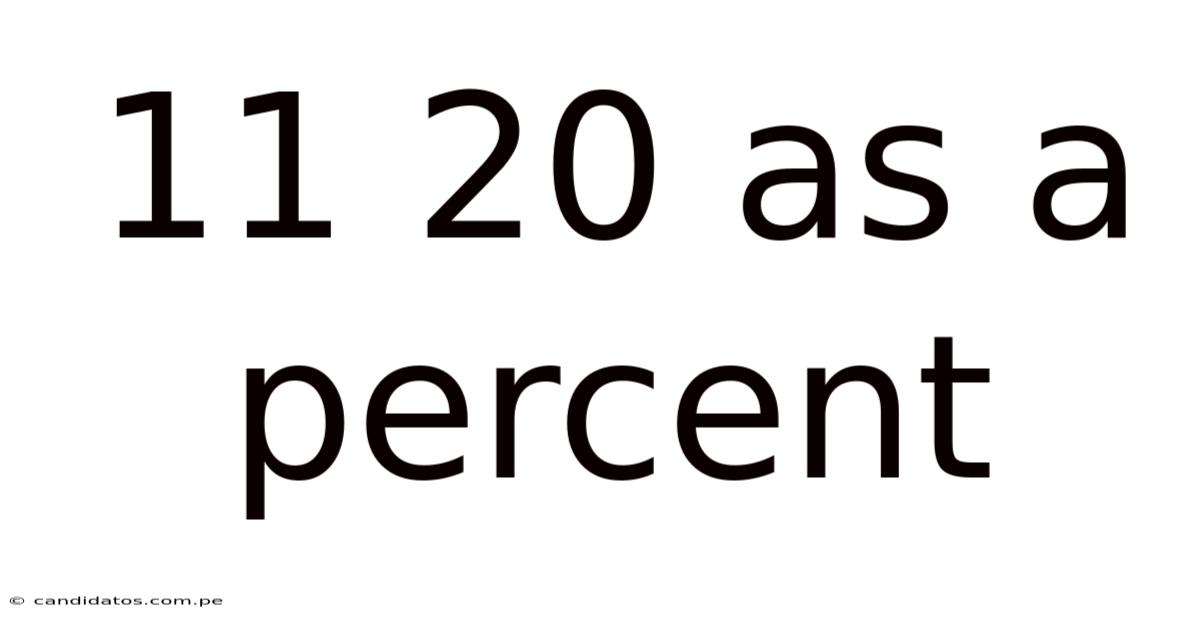
Table of Contents
11/20 as a Percent: A Comprehensive Guide to Understanding Fractions, Decimals, and Percentages
Converting fractions to percentages is a fundamental skill in mathematics with applications across various fields, from finance and statistics to everyday life. This comprehensive guide will walk you through the process of converting the fraction 11/20 into a percentage, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll explore different methods, address common misconceptions, and delve into the broader context of working with fractions, decimals, and percentages.
Introduction: Understanding the Relationship Between Fractions, Decimals, and Percentages
Before we dive into calculating 11/20 as a percentage, let's establish a clear understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: A fraction expresses a part of a whole as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 11/20, 11 represents the part and 20 represents the whole.
-
Decimals: A decimal represents a part of a whole using the base-10 number system. Decimals use a decimal point to separate the whole number part from the fractional part. For instance, 0.5 represents one-half (1/2).
-
Percentages: A percentage represents a part of a whole as a fraction of 100. The symbol "%" is used to denote a percentage. For example, 50% means 50 out of 100, or one-half (1/2).
These three representations are interchangeable. You can convert a fraction to a decimal and then to a percentage, or you can directly convert a fraction to a percentage, and vice-versa.
Method 1: Converting 11/20 to a Percentage Directly
The most straightforward method to convert 11/20 to a percentage involves understanding that a percentage is simply a fraction with a denominator of 100. Therefore, we need to find an equivalent fraction to 11/20 that has 100 as its denominator.
To do this, we ask ourselves: what number do we multiply the denominator (20) by to get 100? The answer is 5 (20 x 5 = 100). Since we must multiply the denominator by 5 to obtain 100, we must also multiply the numerator by the same number to maintain the equivalence of the fraction.
11 x 5 = 55
Therefore, 11/20 is equivalent to 55/100. Since a percentage is a fraction out of 100, 55/100 is equal to 55%.
Method 2: Converting 11/20 to a Decimal, then to a Percentage
Another way to convert 11/20 to a percentage is by first converting it into a decimal. To convert a fraction to a decimal, we simply divide the numerator by the denominator:
11 ÷ 20 = 0.55
Now, to convert the decimal 0.55 to a percentage, we multiply it by 100 and add the percentage symbol:
0.55 x 100 = 55
Therefore, 0.55 is equal to 55%. This method reinforces the understanding that multiplying a decimal by 100 shifts the decimal point two places to the right.
Method 3: Using Proportions to Solve for the Percentage
This method utilizes the concept of proportions to solve for the unknown percentage. We can set up a proportion as follows:
11/20 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
20x = 1100
Now, divide both sides by 20:
x = 1100 ÷ 20 = 55
Therefore, x = 55, meaning 11/20 is equal to 55%. This method highlights the relationship between fractions and proportions, providing a more algebraic approach to solving the problem.
Illustrative Examples: Real-World Applications of Percentage Conversion
Understanding percentage conversion isn't just about abstract mathematical concepts; it's a crucial skill applicable in various real-world situations. Here are a few examples:
-
Grade Calculation: Imagine you answered 11 out of 20 questions correctly on a test. Using our calculation, you achieved a score of 55%.
-
Sales and Discounts: A store offers a 55% discount on an item. This means you'll pay 45% (100% - 55%) of the original price.
-
Financial Analysis: Understanding percentages is crucial for analyzing financial statements, calculating interest rates, and interpreting investment returns. For example, an investment yielding 55% return on investment is highly significant.
-
Data Interpretation: In many fields, data is presented in percentages. Understanding how to convert between fractions and percentages allows for a better interpretation of this data.
Frequently Asked Questions (FAQ)
-
What is the easiest way to convert a fraction to a percentage? The easiest way is often the direct method: find an equivalent fraction with a denominator of 100.
-
Can I convert any fraction to a percentage? Yes, any fraction can be converted to a percentage. However, some fractions might result in repeating or non-terminating decimals, leading to approximate percentage values.
-
What if the fraction has a larger denominator than 100? If the denominator is not a factor of 100, you can still use the division method (converting to a decimal first) to obtain the percentage.
-
Why is understanding percentages important? Percentages provide a standardized way to compare and interpret proportions, making them essential in various fields.
-
Are there online calculators for percentage conversion? Yes, many online calculators can help with percentage conversions, but understanding the underlying process is crucial for building mathematical literacy.
Scientific Explanation: The Mathematical Basis of Percentage Conversion
The conversion from a fraction to a percentage is fundamentally based on the concept of ratios and proportions. A percentage is simply a ratio expressed as a fraction of 100. The process of conversion involves manipulating the fraction to obtain an equivalent fraction with a denominator of 100. This manipulation is done through equivalent fractions, ensuring that the ratio remains constant while changing the representation. The division method (converting to a decimal first) is rooted in the definition of a fraction as a division operation. Multiplying the decimal result by 100 is merely a scaling factor to express the fraction as a percentage—parts per hundred.
The mathematical foundation underpinning percentage conversion is closely linked to the fundamental principles of arithmetic and algebra, including equivalent fractions, ratios, proportions, and decimal operations. A solid grasp of these concepts is crucial not only for performing the conversions accurately but also for understanding the underlying mathematical logic behind the process.
Conclusion: Mastering Percentage Conversions for Success
Converting fractions like 11/20 into a percentage (55%) is a vital skill with wide-ranging applications. This guide has presented multiple methods for performing this conversion, each with its advantages. By mastering these methods and understanding the underlying principles, you'll be well-equipped to tackle similar problems and apply your knowledge to real-world scenarios in various academic and professional settings. Remember, consistent practice is key to building fluency and confidence in working with fractions, decimals, and percentages. The ability to confidently interconvert between these representations will significantly enhance your mathematical proficiency and problem-solving skills.
Latest Posts
Latest Posts
-
Senegals Neighbour To The East
Sep 17, 2025
-
Number Of Neutrons For Potassium
Sep 17, 2025
-
Advantages And Disadvantages Of Coal
Sep 17, 2025
-
Good Adjectives Starting With E
Sep 17, 2025
-
Words With Q U I
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 11 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.