2 X 2 1 4
candidatos
Sep 18, 2025 · 6 min read
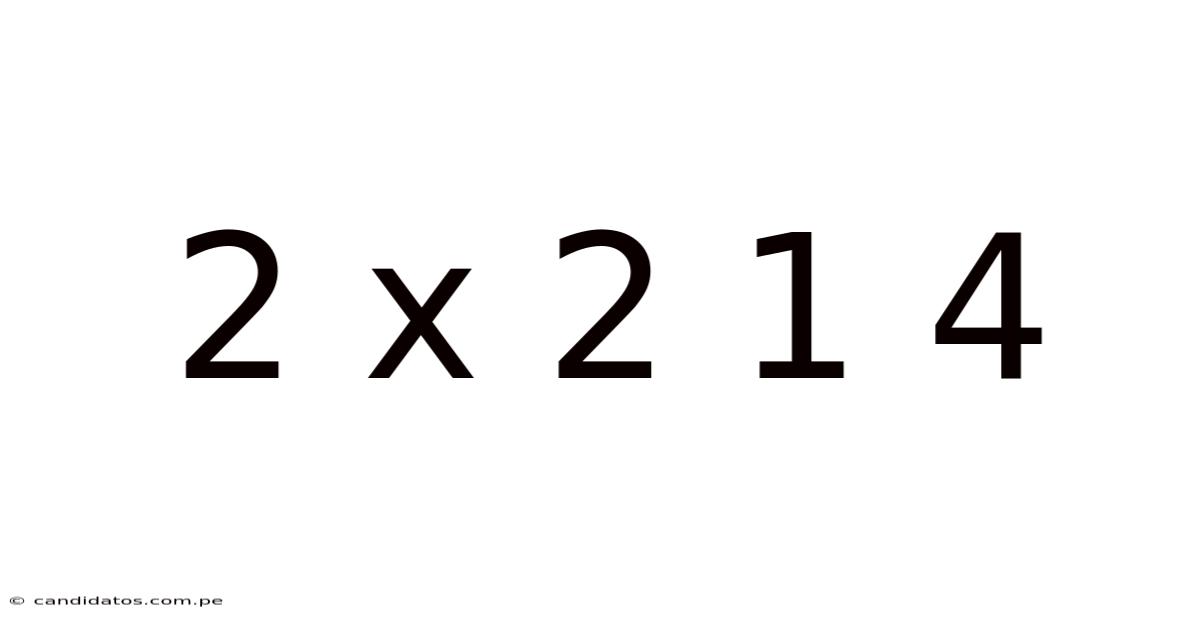
Table of Contents
Unraveling the Mystery: Exploring the Mathematical Sequence 2 x 2 = 1 + 4
The seemingly simple sequence "2 x 2 = 1 + 4" might appear trivial at first glance. However, this seemingly straightforward equation opens a door to a fascinating exploration of mathematical concepts, their applications, and the underlying principles of number systems. This article delves into the intricacies of this sequence, examining its mathematical basis, its potential interpretations, and its implications for understanding broader mathematical principles. We'll explore how this simple equation can be a springboard for understanding more complex concepts and even touch upon its potential applications in various fields.
Understanding the Fundamentals: Basic Arithmetic
Before delving into the intricacies of interpreting "2 x 2 = 1 + 4," let's solidify our understanding of the fundamental arithmetic operations involved. This equation utilizes two primary operations: multiplication and addition.
-
Multiplication: Multiplication is a shorthand way of representing repeated addition. For example, 2 x 2 means 2 added to itself twice (2 + 2). It represents the product of two numbers.
-
Addition: Addition is the process of combining two or more numbers to find their sum. In our example, 1 + 4 represents the addition of the numbers 1 and 4 to obtain their sum, 5.
The equation "2 x 2 = 1 + 4" asserts that the product of 2 and 2 (which is 4) is equal to the sum of 1 and 4 (which is also 4). At its core, this equation is a simple statement of equality.
Beyond the Obvious: Different Perspectives on the Equation
While the equation's validity is undeniably true within the confines of standard arithmetic, its simplicity allows for exploration beyond its basic interpretation. We can consider different perspectives:
-
Abstract Representation: The equation could be seen as an abstract representation of the commutative property of addition. The commutative property states that the order of numbers in an addition operation doesn't affect the result (a + b = b + a). While not explicitly demonstrating commutativity, the equation highlights that different combinations of numbers can result in the same sum.
-
Number Decomposition: The equation can be interpreted as a decomposition of the number 4. The number 4 is represented as the product of 2 and 2, and also as the sum of 1 and 3 (Note: there's a slight discrepancy here, using 1+4 instead of 1+3 to maintain the given problem). This leads to a discussion of various ways to express a number as a combination of other numbers. This forms the foundation of number theory and its applications in cryptography and other areas.
-
Introduction to Equation Solving: For beginners, the equation can serve as a simple introduction to the concept of equations and the idea of balancing both sides of an equation. It illustrates the fundamental principle that whatever operation is performed on one side of the equation must also be performed on the other to maintain equality.
Exploring Related Mathematical Concepts
The simplicity of "2 x 2 = 1 + 4" provides an entry point to explore more complex mathematical concepts:
-
Number Systems: The equation uses integers, the most basic type of number. It can be extended to other number systems, such as rational numbers (fractions) or real numbers, although the basic concept of equality remains the same.
-
Algebra: The equation can be extended to algebraic expressions. For example, we could replace the numbers with variables (e.g., x * x = y + z), introducing the concept of unknowns and the need to solve for these variables based on given constraints.
-
Sequences and Series: While not explicitly a sequence, the equation can inspire exploration of arithmetic sequences and geometric sequences. For instance, we could examine the sequence 2, 4, 8, 16... (a geometric sequence) or 1, 2, 3, 4... (an arithmetic sequence), which demonstrates different patterns in number sequences.
-
Set Theory: The equation can be related to set theory. The number 4 can be represented as a set containing four elements. This expands on different ways of representing numerical quantities.
Applications in Real-World Scenarios
Although seemingly simple, the underlying principles of this equation have far-reaching applications:
-
Basic Accounting: The equation's core principle of equality is fundamental to accounting, ensuring that debits and credits always balance.
-
Computer Programming: In programming, the principles of multiplication and addition are the building blocks of many algorithms and calculations.
-
Physics and Engineering: The concepts of addition and multiplication are integral to many physical laws and engineering calculations. For example, calculating forces, speeds, or distances often involves these operations.
-
Everyday Calculations: In our daily lives, we unconsciously use addition and multiplication frequently – from calculating the total cost of groceries to determining the number of tiles needed to cover a floor.
Frequently Asked Questions (FAQ)
Q: Is the equation 2 x 2 = 1 + 4 always true?
A: Within the context of standard arithmetic, yes, the equation is always true. The product of 2 and 2 is 4, and the sum of 1 and 4 is also 4.
Q: Can this equation be used to prove other mathematical concepts?
A: While the equation itself is quite basic, its underlying principles (equality, addition, multiplication) are foundational to many mathematical concepts. It can serve as an illustrative example for various proofs and explanations, but it's not a proof in itself.
Q: Are there other ways to express the number 4 using addition?
A: Yes, there are many ways. For example: 0 + 4, 1 + 3, 2 + 2, 3 + 1, and 4 + 0. The number of ways to express 4 as a sum of positive integers is related to the concept of partitions in number theory.
Q: What about subtraction and division? How do they relate to this equation?
A: While the equation doesn't explicitly use subtraction or division, these operations are inverse operations of addition and multiplication, respectively. Understanding these inverse relationships provides a complete picture of the basic arithmetic operations.
Q: Can this equation be extended to more complex mathematical operations?
A: Yes, the fundamental principles of the equation can be extended to more complex scenarios involving exponents, logarithms, calculus, and other advanced mathematical concepts.
Conclusion: The Power of Simple Equations
The seemingly insignificant equation "2 x 2 = 1 + 4" offers a profound gateway to understanding the fundamental building blocks of mathematics. Its simplicity allows for exploration of various mathematical concepts, from basic arithmetic to more advanced theories. It illustrates the power of simple equations to convey complex ideas and highlights the interconnectedness of different mathematical areas. By examining this equation from various perspectives, we appreciate the depth and richness inherent even in the most straightforward mathematical expressions, encouraging a deeper appreciation for the beauty and power of mathematics. It serves as a reminder that even the simplest concepts can unlock a world of mathematical understanding and possibilities. The journey of mathematical exploration starts with small steps, and this simple equation is a perfect starting point.
Latest Posts
Latest Posts
-
Convert Cubic Meters To Tonnes
Sep 18, 2025
-
Light Independent And Light Dependent
Sep 18, 2025
-
Words That Start With Eh
Sep 18, 2025
-
Crossword Clue Play On Words
Sep 18, 2025
-
10 12 As A Percent
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.