10 12 As A Percent
candidatos
Sep 18, 2025 · 5 min read
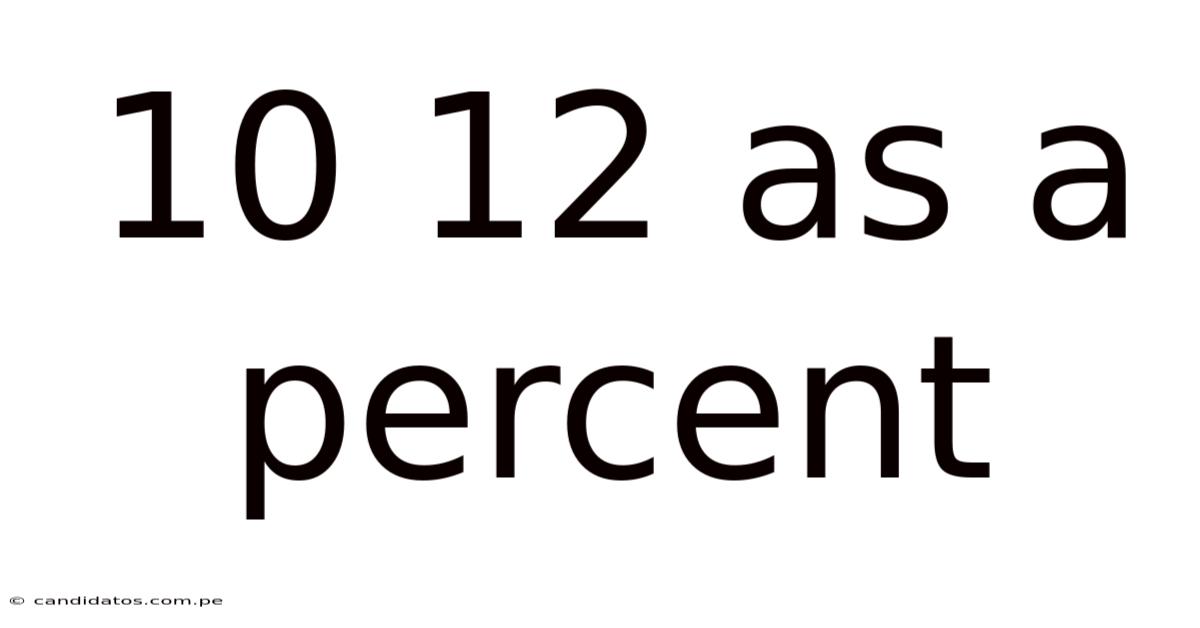
Table of Contents
Understanding 10/12 as a Percentage: A Comprehensive Guide
What does 10/12 as a percent actually mean? This seemingly simple question opens the door to a deeper understanding of percentages, fractions, and their practical applications in everyday life. This comprehensive guide will not only show you how to calculate 10/12 as a percentage but will also explore the underlying mathematical concepts, provide practical examples, and address frequently asked questions. By the end, you'll be confident in converting fractions to percentages and applying this skill in various situations.
Understanding Fractions and Percentages
Before diving into the calculation, let's solidify our understanding of the fundamental concepts involved. A fraction represents a part of a whole. In the fraction 10/12, 10 represents the part and 12 represents the whole. A percentage, on the other hand, expresses a fraction as a portion of 100. The symbol "%" denotes percentage. Therefore, converting a fraction to a percentage involves expressing the fraction's value as a number out of 100.
Calculating 10/12 as a Percentage: Step-by-Step
There are several ways to calculate 10/12 as a percentage. Here's a step-by-step breakdown of the most common methods:
Method 1: Direct Conversion
-
Divide the numerator by the denominator: Divide 10 by 12. This gives you 0.8333... (the decimal representation continues infinitely).
-
Multiply by 100: Multiply the decimal result (0.8333...) by 100 to express it as a percentage. This gives you 83.333...%.
-
Rounding: For practical purposes, you'll usually round the percentage to a specific number of decimal places. Rounding to two decimal places, we get 83.33%.
Method 2: Simplifying the Fraction First
This method involves simplifying the fraction before converting it to a percentage. Simplifying a fraction means reducing it to its lowest terms. Both 10 and 12 are divisible by 2:
-
Simplify the fraction: 10/12 simplifies to 5/6.
-
Divide the numerator by the denominator: Divide 5 by 6, which equals approximately 0.8333.
-
Multiply by 100: Multiply 0.8333 by 100 to get approximately 83.33%.
Both methods yield the same result: 10/12 is approximately 83.33%.
The Importance of Accuracy and Rounding
The decimal representation of 10/12 (0.8333...) is an example of a repeating decimal. This means that the digit 3 repeats infinitely. When converting to a percentage, we often round the decimal to a manageable number of decimal places. The level of accuracy required depends on the context. In some cases, rounding to the nearest whole number (83%) might suffice, while in others, greater precision (83.33%) or even more decimal places might be necessary.
Practical Applications of Percentage Calculations
Understanding how to convert fractions to percentages is crucial in various real-world scenarios:
-
Calculating Grades: If you answered 10 out of 12 questions correctly on a test, your score is 83.33%.
-
Financial Calculations: Percentage calculations are essential for understanding interest rates, discounts, tax rates, and profit margins. For instance, if a store offers a 10% discount on a $12 item, the discount is $1.20 ($12 * 0.10 = $1.20).
-
Data Analysis: Percentages are widely used in data analysis to represent proportions and trends. For example, if a survey shows 10 out of 12 respondents prefer a particular product, this can be expressed as 83.33% preference.
-
Everyday Life: Calculating tips in restaurants, determining sale prices, or understanding the nutritional information on food labels all involve percentage calculations.
Further Exploration: Percentage Increase and Decrease
The concept of percentages extends beyond simple fraction conversion. You can also use percentages to calculate increases and decreases.
-
Percentage Increase: If a value increases from an initial value to a new value, the percentage increase is calculated as: [(New Value - Initial Value) / Initial Value] * 100%.
-
Percentage Decrease: If a value decreases from an initial value to a new value, the percentage decrease is calculated as: [(Initial Value - New Value) / Initial Value] * 100%.
For example, if the price of an item increased from $10 to $12, the percentage increase is: [($12 - $10) / $10] * 100% = 20%.
Beyond 10/12: Mastering Fraction-to-Percentage Conversions
The principles used to convert 10/12 to a percentage are applicable to any fraction. To convert any fraction a/b to a percentage, follow these steps:
- Divide a by b.
- Multiply the result by 100.
- Round to the desired number of decimal places (if necessary).
Frequently Asked Questions (FAQ)
Q: Why is it important to simplify fractions before converting to a percentage?
A: Simplifying fractions makes the calculation easier and reduces the risk of errors, particularly when dealing with larger numbers. It also allows for a clearer understanding of the fraction's value.
Q: What if the fraction has a decimal in the numerator or denominator?
A: Convert the decimal to a fraction first. For example, if you have 2.5/5, convert 2.5 to the fraction 5/2, resulting in (5/2)/5 = 1/2 = 50%.
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have functions to perform division and multiplication, making the conversion process straightforward. Many calculators even have a dedicated percentage function.
Q: Are there any online tools or resources to help with percentage calculations?
A: Many websites and apps offer free online calculators specifically designed for percentage conversions and other mathematical calculations.
Q: What is the difference between a fraction and a ratio?
A: While both fractions and ratios compare quantities, a fraction represents a part of a whole, while a ratio compares two or more quantities. For example, 10/12 is a fraction, but the ratio of boys to girls in a class might be 10:12 (or simplified to 5:6).
Conclusion
Converting fractions to percentages is a fundamental skill with broad applications. Understanding the underlying principles, as illustrated by the conversion of 10/12 to approximately 83.33%, enables you to confidently tackle similar problems in various contexts. Remember to choose an appropriate level of rounding based on the context of your calculation, and don’t hesitate to utilize calculators or online resources to assist you in the process. Mastering percentage calculations empowers you to approach numerical problems with greater precision and confidence. By practicing these methods and understanding the reasoning behind them, you'll become proficient in working with percentages and their various applications.
Latest Posts
Latest Posts
-
National Game Of Sri Lanka
Sep 18, 2025
-
Net For A 3d Shape
Sep 18, 2025
-
3000 Sq Feet In Meters
Sep 18, 2025
-
2019 Methods Exam 1 Solutions
Sep 18, 2025
-
5 X 4 X 3
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 10 12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.