2 3 Divided By 12
candidatos
Sep 23, 2025 · 5 min read
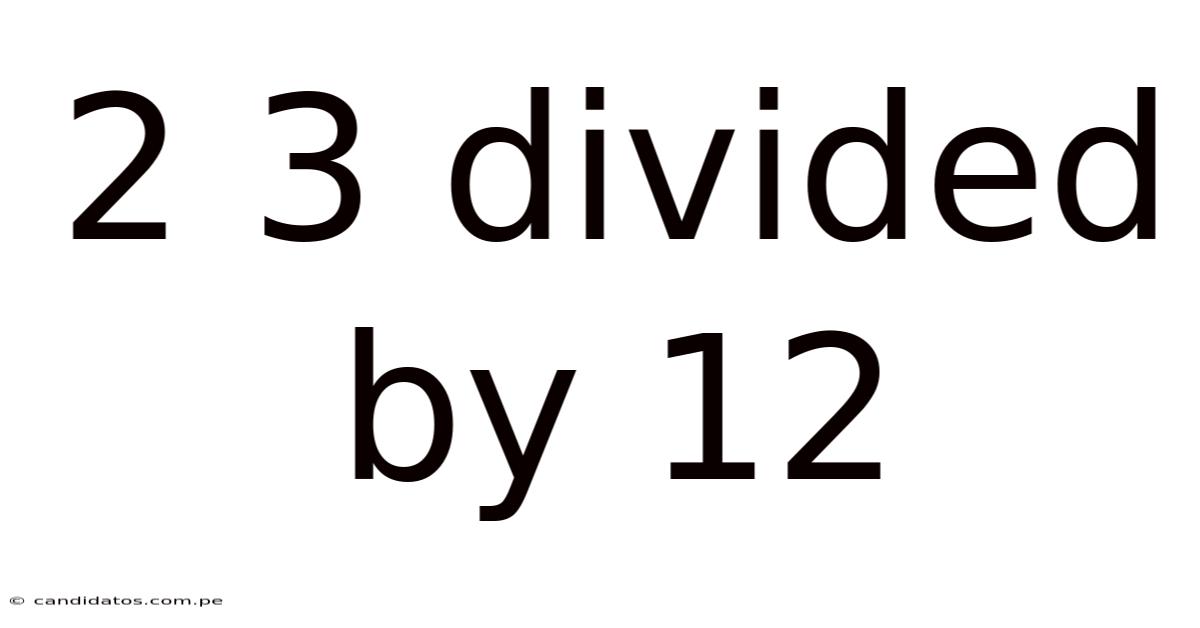
Table of Contents
Decoding the Mystery: 2/3 Divided by 12
Understanding fractions and division can sometimes feel like navigating a maze. This article will demystify the seemingly complex problem of 2/3 divided by 12, providing a step-by-step guide, insightful explanations, and addressing frequently asked questions. By the end, you'll not only know the answer but also possess a deeper understanding of the underlying mathematical principles. This will empower you to tackle similar problems with confidence and ease.
Introduction: A Friendly Approach to Fractions and Division
The question, "What is 2/3 divided by 12?", might seem daunting at first glance. However, with a systematic approach and a clear understanding of the concepts involved, solving it becomes surprisingly straightforward. This guide will break down the problem into manageable steps, using clear language and helpful examples to ensure a comprehensive understanding for everyone, regardless of their mathematical background. We'll explore the fundamental rules of fraction division, and show how they apply to this specific problem.
Understanding the Fundamentals: Fractions and Division
Before diving into the solution, let's revisit the basics. A fraction represents a part of a whole. The top number is the numerator (in this case, 2), indicating how many parts we have. The bottom number is the denominator (3), showing how many equal parts the whole is divided into.
Division, on the other hand, involves splitting a quantity into equal groups. When dividing fractions, we're essentially asking: "How many times does one fraction fit into another?"
Step-by-Step Solution: 2/3 ÷ 12
Here's how to solve 2/3 divided by 12 step-by-step:
Step 1: Rewrite the Division as a Multiplication
The key to dividing fractions is to transform the division problem into a multiplication problem. To do this, we keep the first fraction (2/3) as it is, change the division sign (÷) to a multiplication sign (×), and invert (or take the reciprocal of) the second number (12). Remember, 12 can be written as the fraction 12/1. Inverting 12/1 gives us 1/12.
So, our problem becomes: (2/3) × (1/12)
Step 2: Multiply the Numerators and Denominators
Now, we multiply the numerators together and the denominators together separately:
Numerators: 2 × 1 = 2 Denominators: 3 × 12 = 36
This gives us the fraction 2/36.
Step 3: Simplify the Fraction
The fraction 2/36 can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 2 and 36 is 2. We divide both the numerator and the denominator by the GCD:
2 ÷ 2 = 1 36 ÷ 2 = 18
Therefore, the simplified fraction is 1/18.
Conclusion of the Step-by-Step Solution: 2/3 divided by 12 equals 1/18.
Visualizing the Problem: A Real-World Analogy
Imagine you have a pizza cut into 3 equal slices. You have 2 of those slices (2/3 of the pizza). Now, you want to share these 2 slices equally among 12 people. How much pizza does each person get?
Each person would receive 1/18th of the whole pizza. This perfectly illustrates the result we obtained through our calculations.
The Mathematical Explanation: Why Does This Work?
The process of inverting and multiplying when dividing fractions is rooted in the concept of reciprocals. The reciprocal of a number is the value that, when multiplied by the original number, results in 1. For example, the reciprocal of 12 is 1/12 (because 12 × 1/12 = 1).
When we divide by a fraction, we are essentially asking how many times that fraction fits into the first number. Inverting and multiplying allows us to find that answer accurately. This method maintains mathematical consistency and ensures we arrive at the correct solution.
Handling More Complex Problems: Expanding the Concept
The principles demonstrated in solving 2/3 ÷ 12 are applicable to a wide range of fraction division problems. Regardless of the complexity, the steps remain consistent:
-
Convert any whole numbers into fractions: This allows you to apply the same rules to all numbers involved.
-
Rewrite the division as multiplication: Invert (reciprocate) the second fraction.
-
Multiply numerators and denominators: Calculate the new numerator and denominator separately.
-
Simplify the resulting fraction: Reduce the fraction to its lowest terms.
Frequently Asked Questions (FAQs)
Q1: Can I divide 12 by 2/3 instead?
A1: Yes, you can! However, remember to invert and multiply. The problem would then become 12/1 × 3/2 = 36/2 = 18. This shows the reciprocal relationship – dividing by 2/3 is the same as multiplying by 3/2, which results in the inverse of the previous answer (1/18 vs. 18).
Q2: What if the fractions involved are improper fractions (where the numerator is greater than the denominator)?
A2: The process remains the same. Follow the steps outlined above, and you can simplify the resulting fraction as needed.
Q3: What if I get a mixed number as an answer?
A3: A mixed number combines a whole number and a fraction (e.g., 2 1/2). If your answer is a mixed number, you might need to convert it to an improper fraction for some applications or leave it in mixed number form if that's more practical.
Q4: Are there any alternative methods to solve this problem?
A4: While the invert-and-multiply method is generally the most efficient, you could also convert the fractions into decimals and then perform the division. However, this approach might lead to rounding errors and doesn't demonstrate a fundamental understanding of fraction manipulation.
Conclusion: Mastering Fraction Division
Solving 2/3 divided by 12 may have seemed daunting at the outset, but by understanding the underlying principles of fractions and division, and by following a systematic approach, we successfully determined the answer to be 1/18. This process, although seemingly simple for this particular problem, lays the groundwork for solving more complex fractional equations. Remember the key steps: rewrite the division as multiplication, invert the second fraction, multiply, and simplify. Mastering these concepts empowers you to confidently tackle a vast range of mathematical problems involving fractions, building a solid foundation for further mathematical exploration. Keep practicing, and you'll find that working with fractions becomes increasingly intuitive and enjoyable.
Latest Posts
Latest Posts
-
35 37 As A Percentage
Sep 23, 2025
-
Days Of The Week Worksheet
Sep 23, 2025
-
Electrical Fuses Vs Circuit Breakers
Sep 23, 2025
-
Describing Words Beginning With F
Sep 23, 2025
-
Calcium Carbonate And Nitric Acid
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.