35 37 As A Percentage
candidatos
Sep 23, 2025 · 5 min read
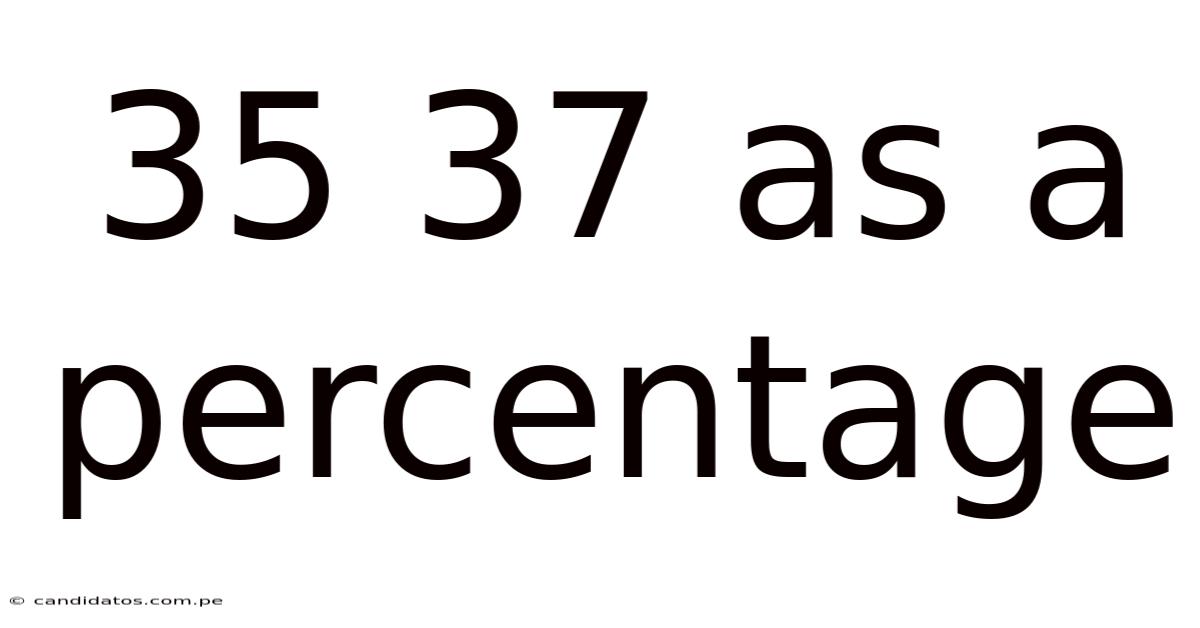
Table of Contents
Decoding the Percentage: Understanding 35 out of 37
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. This article dives deep into understanding how to calculate and interpret the percentage represented by 35 out of 37, exploring the process step-by-step, providing context for different applications, and addressing frequently asked questions. We'll unpack the mathematics behind the calculation, explain its significance, and illustrate its practical uses. This comprehensive guide will empower you to confidently tackle similar percentage calculations in the future.
Understanding the Fundamentals of Percentage Calculations
Before we delve into the specifics of 35 out of 37, let's establish a clear understanding of percentage calculations. A percentage is simply a fraction expressed as a part of 100. The term "percent" literally means "per hundred". The fundamental formula for calculating a percentage is:
(Part / Whole) * 100% = Percentage
In this formula:
- Part: Represents the specific value you are interested in expressing as a percentage. In our example, this is 35.
- Whole: Represents the total value to which the part belongs. In our example, the whole is 37.
- Percentage: The resulting value, representing the part as a proportion of the whole, expressed as a percentage.
Calculating 35 out of 37 as a Percentage
Now let's apply this formula to our specific problem: calculating what percentage 35 represents out of 37.
-
Identify the Part and the Whole: We have already identified the part as 35 and the whole as 37.
-
Divide the Part by the Whole: Divide 35 by 37: 35 / 37 ≈ 0.9459
-
Multiply by 100: Multiply the result by 100 to express the fraction as a percentage: 0.9459 * 100% ≈ 94.59%
Therefore, 35 out of 37 is approximately 94.59%.
Contextualizing the Result: Interpreting the Percentage
The percentage 94.59% signifies that 35 represents a substantial portion – almost the entirety – of 37. The context in which this percentage arises is crucial for accurate interpretation. For example:
- Academic Performance: If 35 out of 37 questions were answered correctly on a test, a score of 94.59% indicates excellent performance.
- Sales Targets: If a salesperson achieved 35 out of a target of 37 sales, they nearly met their goal, with only a small shortfall.
- Project Completion: If 35 out of 37 tasks in a project were completed, the project is nearing completion with only a few minor tasks remaining.
- Survey Results: If 35 out of 37 respondents answered “yes” to a particular question in a survey, this indicates strong positive sentiment towards the subject.
The interpretation of 94.59% will vary depending on the specific scenario. The significance of being close to 100% versus the small difference between 35 and 37 should be considered within the specific context.
Beyond the Calculation: Exploring Related Concepts
Understanding the percentage calculation of 35 out of 37 opens doors to exploring other related concepts in mathematics and statistics. These include:
-
Proportions: The calculation demonstrates a fundamental concept of proportions – the relationship between two quantities. Understanding proportions is essential for solving many real-world problems, including scaling recipes, converting units, and analyzing data.
-
Ratios: Closely related to proportions, ratios express the relationship between two or more quantities. The ratio of 35 to 37 can be written as 35:37, providing another way to represent the relationship between the two numbers.
-
Fractions: The core of percentage calculations lies in understanding fractions. 35/37 is a fraction representing the part compared to the whole. Mastering fractions is crucial for handling percentages effectively.
-
Decimals: The decimal equivalent of 0.9459 is used in the percentage calculation. Understanding decimals helps translate between fractions, percentages, and decimal representations of numbers.
-
Statistical Significance: In statistical analysis, determining whether a difference is statistically significant often involves percentage calculations and comparisons. In the context of the 35 out of 37 example, the closeness to 100% could be analyzed statistically to determine its significance.
Practical Applications of Percentage Calculations
The ability to calculate percentages is indispensable in a wide range of applications:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and returns on investments all rely heavily on percentage calculations.
- Business: Analyzing sales data, market share, customer satisfaction, and productivity often involves calculating and interpreting percentages.
- Science: Expressing experimental results, analyzing data, and comparing measurements often require percentage calculations.
- Education: Grading tests, calculating averages, and tracking student progress rely on percentage calculations.
- Everyday Life: Budgeting, tipping in restaurants, calculating discounts, and understanding interest rates on loans all involve using percentages.
Frequently Asked Questions (FAQ)
Q1: How do I calculate percentages quickly without a calculator?
A1: For quick estimations, you can use rounding techniques. Rounding 37 to 40 simplifies the calculation: 35/40 = 0.875, which is approximately 87.5%. While less precise, this provides a rapid estimate.
Q2: What if the "whole" number is zero?
A2: You cannot calculate a percentage when the whole is zero because division by zero is undefined in mathematics. It means there's no basis for comparison.
Q3: Can percentages exceed 100%?
A3: Yes, percentages can exceed 100%. This occurs when the part is larger than the whole. For example, if you have 120 apples and your expected amount was 100, you exceeded your expectation by 20%, or 120% of the expected amount.
Q4: Are there any online tools for calculating percentages?
A4: Many online calculators and software programs provide percentage calculation functions. These tools can be helpful for verifying results or handling more complex calculations.
Q5: How can I improve my understanding of percentage calculations?
A5: Practice is key. Work through various percentage problems, starting with simpler examples and gradually increasing complexity. Use online resources and textbooks to reinforce your understanding.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that enhances both academic and professional success. The detailed explanation and step-by-step guide provided in this article demonstrate the process of calculating 35 out of 37 as a percentage, approximately 94.59%. We have explored the formula, its practical applications, and clarified some frequently asked questions. By understanding the principles discussed here, you will be well-equipped to confidently tackle future percentage calculations and apply this fundamental skill across various contexts. Remember that understanding the context is as important as the calculation itself for accurate interpretation and effective application.
Latest Posts
Latest Posts
-
Picture Of A Crow Bird
Sep 23, 2025
-
4 7 As A Percentage
Sep 23, 2025
-
Dividing Decimals By Decimals Worksheet
Sep 23, 2025
-
Is Domain X Or Y
Sep 23, 2025
-
First Flush In Rainwater Harvesting
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 35 37 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.