1 X 2 Y 2
candidatos
Sep 22, 2025 · 6 min read
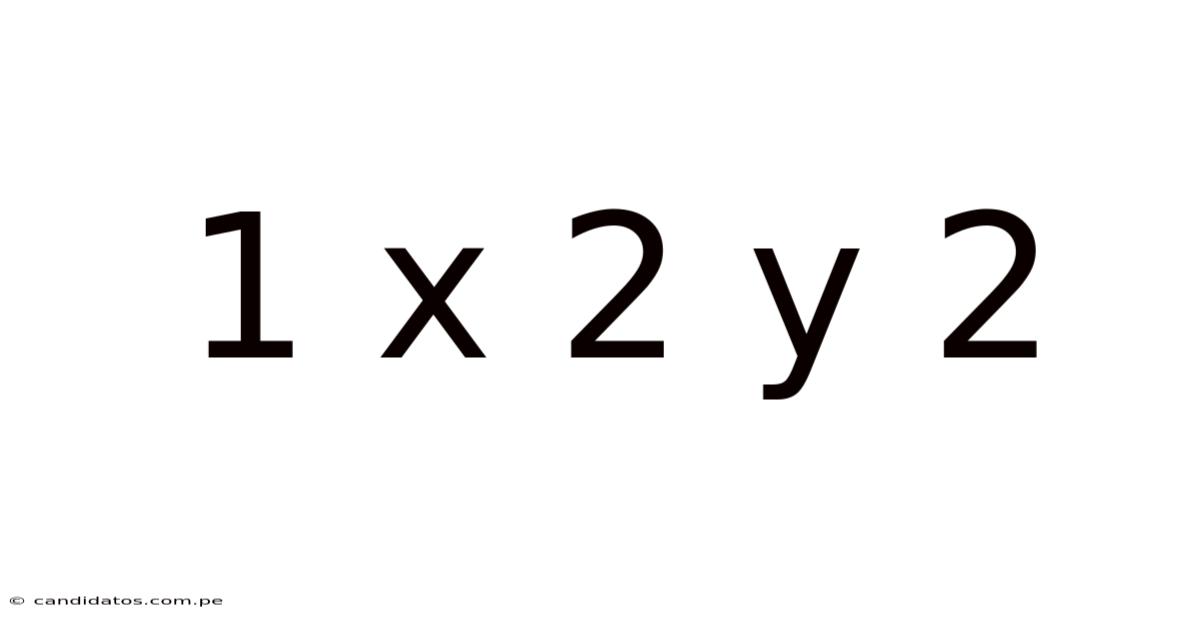
Table of Contents
Decoding the Mystery: A Deep Dive into the Equation 1x² + 2y²
The seemingly simple equation, 1x² + 2y² (or more commonly written as x² + 2y²), might appear innocuous at first glance. However, this quadratic form holds a surprising depth, revealing connections to number theory, geometry, and even abstract algebra. This article will explore this equation comprehensively, delving into its properties, solutions, graphical representation, and its significance in various mathematical fields. We will uncover its secrets, starting from basic understanding and progressing to more advanced concepts, ensuring accessibility for a broad audience.
Introduction: Understanding the Basics
The equation x² + 2y² represents a quadratic form, a homogeneous polynomial of degree two in two variables. This means it's a combination of squared terms (x² and y²) with constant coefficients (1 and 2). Understanding its solutions means finding pairs of integers (x, y) that satisfy the equation. This might seem straightforward, but the nature of solutions depends heavily on the context – are we looking for integer solutions, rational solutions, or real solutions? This distinction will be crucial throughout our exploration.
Finding Integer Solutions: A Number Theoretic Approach
Finding integer solutions to x² + 2y² is a classic problem in number theory. Unlike simpler equations, there's no single, easily stated formula to generate all solutions. Instead, we need to employ techniques that leverage the properties of integers and their factors.
Let's start with some simple examples:
- If x = 1 and y = 0, then 1² + 2(0)² = 1, which satisfies the equation.
- If x = 0 and y = 1, then 0² + 2(1)² = 2, which also satisfies the equation.
- If x = 1 and y = 1, then 1² + 2(1)² = 3.
- If x = 2 and y = 1, then 2² + 2(1)² = 6.
- If x = 3 and y = 0, then 3² + 2(0)² = 9.
- If x = 3 and y = 1, then 3² + 2(1)² = 11.
- If x = 1 and y = 2, then 1² + 2(2)² = 9.
Notice a pattern isn't immediately apparent. To systematically find integer solutions, we can leverage concepts like prime factorization and unique factorization domains. We are essentially searching for numbers that can be expressed as the sum of a perfect square and twice another perfect square.
A deeper dive reveals a connection to the ring of Gaussian integers (numbers of the form a + bi, where a and b are integers and i is the imaginary unit). The equation x² + 2y² can be factored in the Gaussian integers as (x + iy√2)(x - iy√2). The properties of prime factorization in this ring offer powerful tools for analyzing the equation’s solutions, but this requires a significant understanding of abstract algebra.
Graphical Representation: Visualizing the Equation
Moving beyond integer solutions, let's consider the graphical representation of x² + 2y² = k, where k is a constant. This equation represents a family of ellipses centered at the origin (0,0).
-
k > 0: For positive values of k, the equation represents an ellipse. The larger the value of k, the larger the ellipse. The semi-major axis will be along the x-axis, and the semi-minor axis will be along the y-axis, reflecting the coefficients of the equation.
-
k = 0: The only solution is (0, 0).
-
k < 0: There are no real solutions because the sum of two squares cannot be negative.
The graphical representation provides a visual context for understanding the solutions. Integer solutions correspond to points on the ellipse with integer coordinates. The density of these points varies depending on the value of k.
Exploring Rational Solutions: Extending the Scope
While integer solutions are often the focus, we can also explore rational solutions – solutions where x and y are rational numbers (fractions). The nature of rational solutions is closely tied to the integer solutions. If we find a rational solution (x,y), we can multiply both x and y by a suitable integer to obtain an integer solution. This reveals a strong connection between the sets of integer and rational solutions.
The Equation in Different Mathematical Contexts
The equation x² + 2y² appears in various mathematical contexts, far beyond basic number theory.
-
Diophantine Equations: This equation is a prime example of a Diophantine equation, an equation where solutions are restricted to integers. Diophantine equations are notoriously challenging, and the equation x² + 2y² provides a relatively approachable entry point into this rich area of mathematics.
-
Quadratic Forms and Number Theory: As a quadratic form, it's studied extensively in the context of quadratic form theory, a branch of number theory that deals with the properties and representations of quadratic forms over various rings.
-
Geometry of Numbers: In geometry of numbers, this equation relates to lattice points within ellipses, leading to questions about the distribution of integer solutions and their asymptotic behavior.
-
Algebraic Number Theory: The equation is deeply connected with algebraic number theory, particularly through the study of quadratic fields and their associated rings of integers.
Frequently Asked Questions (FAQ)
-
Q: Is there a general formula for finding all integer solutions to x² + 2y² = n? A: No, there's no single, elegant formula for all n. However, methods based on the unique factorization of integers in the ring of Gaussian integers can help determine solutions for specific values of n.
-
Q: How does the coefficient 2 affect the solutions? A: The coefficient 2 fundamentally alters the nature of the solutions. Changing it to another coefficient would lead to a different set of solutions, often with drastically different properties.
-
Q: What are some applications of solving this equation? A: While direct applications may not be immediately obvious, understanding the properties of such equations is crucial for advancements in cryptography, coding theory, and other areas that rely on number theory.
-
Q: Can this equation be generalized to higher dimensions? A: Yes, this equation can be extended to higher dimensions, resulting in more complex equations involving multiple variables and coefficients. The study of these generalizations continues to be a rich area of mathematical research.
Conclusion: A Journey into Mathematical Depth
The seemingly simple equation x² + 2y² opens up a fascinating world of mathematical exploration. From its humble beginnings as a quadratic form, it unveils connections to number theory, geometry, and abstract algebra, showcasing the interconnectedness of mathematical concepts. While finding all integer solutions might not yield a simple formula, the techniques employed to investigate them offer valuable insights into the structure of integers and the power of mathematical tools. This exploration is a testament to the richness and complexity hidden within seemingly simple mathematical expressions, reminding us that even the most basic-looking equations can lead us down a path of profound mathematical discovery. Further research into Gaussian integers, quadratic forms, and related number theory concepts will provide a deeper appreciation for the intricate beauty of this equation.
Latest Posts
Latest Posts
-
Formal Definition Of A Limit
Sep 22, 2025
-
Are Hedgehogs And Echidnas Related
Sep 22, 2025
-
Afghanistan Currency To Indian Rupees
Sep 22, 2025
-
List Of Australian Military Exercises
Sep 22, 2025
-
Colour That Starts With W
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.