15 Percent As A Fraction
candidatos
Sep 16, 2025 · 6 min read
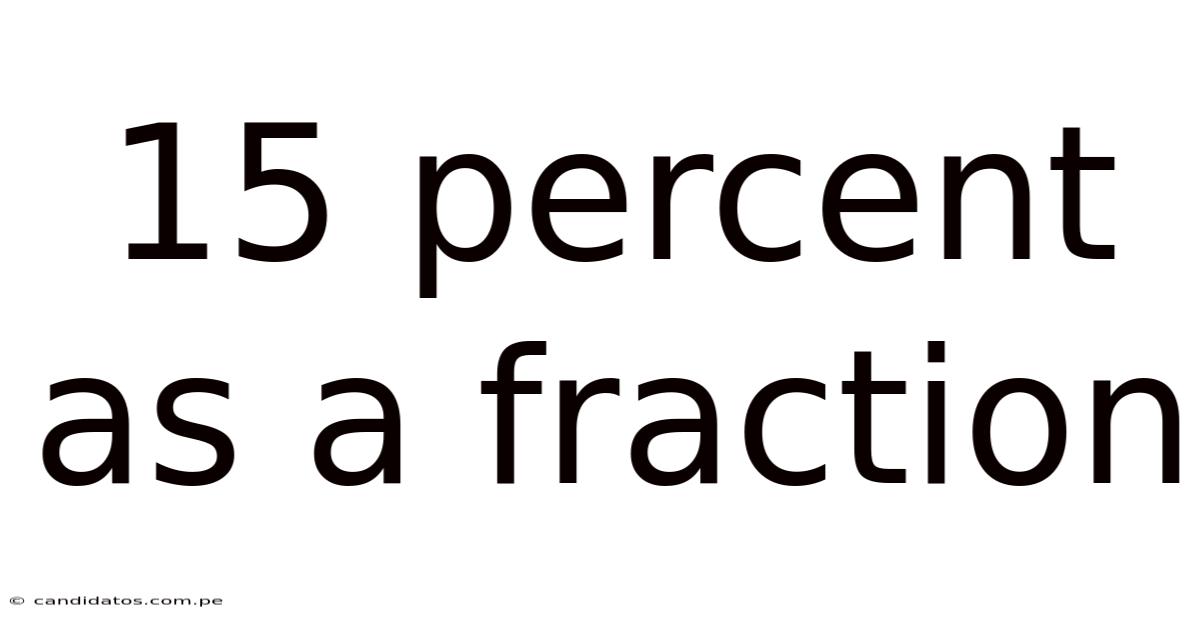
Table of Contents
15 Percent as a Fraction: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics and everyday life. Whether you're calculating discounts, understanding tax rates, or analyzing data, the ability to convert percentages to fractions and decimals is crucial. This article provides a comprehensive guide on how to express 15 percent as a fraction, explaining the process step-by-step and delving into the broader concepts of percentages, fractions, and decimals. We'll also explore some real-world applications and address common questions.
Introduction: Understanding Percentages and Fractions
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 15 percent (15%) means 15 out of 100.
A fraction, on the other hand, represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, 1/2 represents one part out of two equal parts.
Converting between percentages and fractions is a straightforward process, and understanding this conversion is key to solving various mathematical problems.
Converting 15% to a Fraction: A Step-by-Step Guide
The process of converting 15% to a fraction is simple and involves these steps:
-
Write the percentage as a fraction with a denominator of 100: Since a percentage is a fraction of 100, we can write 15% as 15/100.
-
Simplify the fraction: The fraction 15/100 can be simplified by finding the greatest common divisor (GCD) of the numerator (15) and the denominator (100). The GCD of 15 and 100 is 5. We divide both the numerator and the denominator by 5:
15 ÷ 5 = 3 100 ÷ 5 = 20
This simplifies the fraction to 3/20.
Therefore, 15% as a fraction is 3/20.
Further Exploration: Equivalent Fractions
It's important to understand that a fraction can have many equivalent forms. While 3/20 is the simplest form of the fraction representing 15%, there are other fractions that are equivalent to 3/20. For example, if you multiply both the numerator and the denominator by 2, you get 6/40. Multiplying by 3 gives you 9/60, and so on. All these fractions represent the same value as 3/20 and, therefore, the same value as 15%.
The key is to always simplify the fraction to its lowest terms to obtain the most concise and easily understandable representation.
Illustrative Examples: Real-World Applications
Let's consider some real-world scenarios where understanding 15% as a fraction (3/20) is helpful:
-
Discounts: A store offers a 15% discount on an item. If the original price is $100, the discount amount is 15% of $100, which is (3/20) * $100 = $15. This clearly shows the ease of calculating a percentage discount using the fractional representation.
-
Taxes: A sales tax rate is 15%. For a $200 purchase, the tax amount would be (3/20) * $200 = $30.
-
Surveys and Statistics: If 15% of 200 people surveyed prefer a particular brand, the number of people who prefer that brand is (3/20) * 200 = 30 people.
These examples highlight how the fractional representation of 15% (3/20) provides a simpler and more intuitive way to perform calculations compared to directly using the percentage.
Beyond the Basics: Connecting Percentages, Fractions, and Decimals
It’s crucial to understand the interrelationship between percentages, fractions, and decimals. They are simply different ways of representing the same portion of a whole.
-
Percentage to Decimal: To convert a percentage to a decimal, simply divide the percentage by 100. For 15%, this means 15/100 = 0.15.
-
Fraction to Decimal: To convert a fraction to a decimal, divide the numerator by the denominator. For 3/20, this is 3 ÷ 20 = 0.15.
-
Decimal to Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%). For 0.15, this is 0.15 * 100 = 15%.
This interconnectedness allows for flexibility in calculations. You can choose the most convenient representation (percentage, fraction, or decimal) depending on the specific problem and your preferred method of calculation.
Mathematical Properties and Operations
Understanding the mathematical properties of fractions is crucial when working with percentages represented as fractions. Here are some key aspects:
-
Addition and Subtraction: When adding or subtracting fractions, you need a common denominator. For instance, adding 3/20 and 1/5 requires converting 1/5 to 4/20, resulting in a sum of 7/20.
-
Multiplication and Division: Multiplying fractions involves multiplying the numerators and denominators separately. Dividing fractions involves inverting the second fraction and then multiplying.
-
Simplification: Always simplify fractions to their lowest terms to make them easier to work with and interpret.
Mastering these properties enables more efficient and accurate calculations involving percentages expressed as fractions.
Frequently Asked Questions (FAQ)
Q1: Why is it important to simplify fractions?
A1: Simplifying fractions makes them easier to understand and work with. A simplified fraction provides the most concise representation of the value. It also simplifies subsequent calculations.
Q2: Can I convert any percentage to a fraction?
A2: Yes, you can convert any percentage to a fraction by writing it as a fraction with a denominator of 100 and then simplifying.
Q3: What if the percentage is a decimal, like 15.5%?
A3: You can follow the same process. Write it as 15.5/100. To simplify, you can multiply both numerator and denominator by 10 to get 155/1000. Then, find the greatest common divisor and simplify further. In this case, the simplified fraction is 31/200.
Q4: Are there any online tools to help with percentage to fraction conversions?
A4: While this article provides the methodology, various online calculators and converters are available to assist with percentage to fraction conversions if needed.
Q5: How does understanding this help me in real life?
A5: Understanding percentage-to-fraction conversions helps in many everyday situations, including calculating discounts, understanding tax rates, interpreting statistical data, and solving various mathematical problems in finance, cooking, and more.
Conclusion: Mastering the Conversion of 15% to a Fraction
Converting 15% to a fraction, yielding 3/20, is a fundamental skill with far-reaching applications. This process, along with understanding the interconnectedness of percentages, fractions, and decimals, empowers you to tackle numerous mathematical problems confidently and efficiently. The ability to switch between these representations allows for flexibility and enhances your problem-solving capabilities in various academic and real-world situations. Remember the steps, practice the conversions, and embrace the versatility of these mathematical concepts. By understanding this seemingly simple conversion, you unlock a world of mathematical possibilities. From calculating simple discounts to comprehending complex statistical analyses, the foundation laid by mastering this conversion is invaluable.
Latest Posts
Latest Posts
-
1 000 Divided By 10
Sep 16, 2025
-
100 000 Rupees To Dollars
Sep 16, 2025
-
Descriptive Words Beginning With H
Sep 16, 2025
-
Are All Squares Are Rhombuses
Sep 16, 2025
-
Conversion Metres To Square Metres
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.