1 000 Divided By 10
candidatos
Sep 16, 2025 · 6 min read
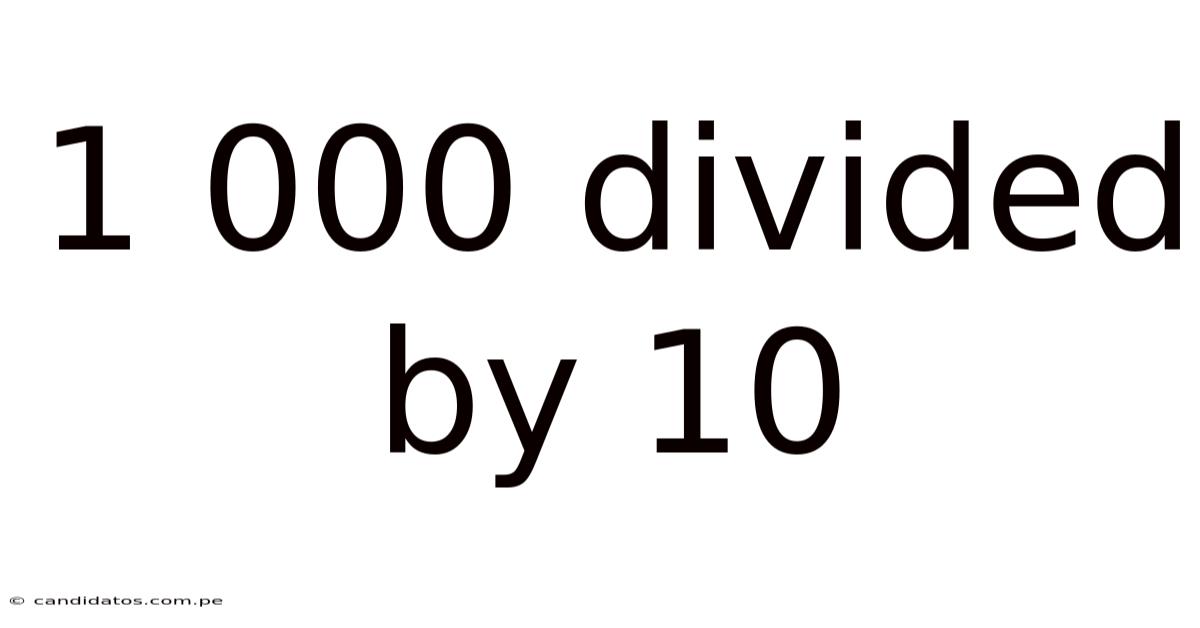
Table of Contents
Unveiling the Simplicity: 1,000 Divided by 10 – A Deep Dive into Division
Dividing 1,000 by 10 might seem like a simple arithmetic problem, suitable only for elementary school students. However, beneath the surface of this seemingly straightforward calculation lies a wealth of mathematical concepts that extend far beyond the basic operation itself. This article will explore not just the answer to 1,000 divided by 10, but also the underlying principles of division, its practical applications, and how it relates to other mathematical ideas. We will delve into different methods of solving this problem, examine its significance in various fields, and address frequently asked questions. This comprehensive guide will leave you with a thorough understanding of this fundamental concept, equipping you to tackle more complex division problems with confidence.
Understanding Division: The Foundation
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts or groups. In the context of 1,000 divided by 10 (written as 1000 ÷ 10 or 1000/10), we are asking: "How many times does 10 fit into 1,000?" The answer, as we'll see shortly, reveals the number of groups of 10 that are contained within 1,000.
This seemingly simple question has profound implications. Think about dividing a collection of 1,000 apples into 10 equal baskets. Each basket would receive an equal number of apples – the result of our division problem. Similarly, if you have 1,000 dollars to distribute equally among 10 people, each person would receive the same amount. Division allows us to solve problems involving equal sharing and partitioning.
Calculating 1,000 Divided by 10: Multiple Approaches
There are several ways to solve 1,000 ÷ 10. Let's explore a few:
-
Long Division: This traditional method is a systematic approach to division, suitable for more complex problems. While it might seem overkill for 1,000 ÷ 10, understanding the process is crucial for tackling larger numbers. The steps would involve:
- Setting up the problem: 10 | 1000
- Determining how many times 10 goes into 10 (the first digit of 1000). The answer is 1.
- Placing the 1 above the 10 in 1000.
- Multiplying 1 by 10, which is 10.
- Subtracting 10 from 10, resulting in 0.
- Bringing down the next digit (0).
- Repeating steps 2-6 until all digits are processed. You will continue to bring down zeros and get a zero remainder.
-
Short Division: For simpler problems like this, short division provides a quicker solution. You can mentally divide 1000 by 10, considering the effect on the zeros.
-
Using Multiplication: Since division is the inverse of multiplication, we can think, "What number, when multiplied by 10, equals 1,000?" The answer is, of course, 100. This method highlights the interconnectedness of arithmetic operations.
-
Cancelling Zeros: A more intuitive method for this specific problem leverages the properties of zeros. Notice that 1,000 has three zeros, and 10 has one zero. We can cancel one zero from both the numerator (1,000) and the denominator (10), leaving us with 100 ÷ 1. This simplifies the calculation to 100.
Regardless of the method employed, the answer remains consistent: 1,000 ÷ 10 = 100.
Beyond the Calculation: Real-World Applications
The seemingly simple act of dividing 1,000 by 10 has far-reaching consequences in various real-world scenarios. Here are a few examples:
-
Finance: Imagine you're splitting a $1,000 bonus among 10 employees. Each employee receives $100. This principle applies to various financial calculations, such as distributing profits, calculating per-unit costs, or dividing investments.
-
Measurement: Converting units often involves division. For instance, converting 1,000 centimeters to meters requires dividing by 100 (since there are 100 centimeters in a meter). While this isn't directly 1,000 ÷ 10, the underlying principle remains the same: partitioning a larger quantity into smaller, equal units.
-
Data Analysis: In statistics and data analysis, dividing large datasets into smaller, manageable groups is essential for efficient processing and interpretation. Understanding division helps in calculating averages, percentages, and proportions.
-
Engineering and Construction: Calculating material quantities, distributing workloads, and managing resources all involve division. For instance, if you need 1,000 bricks and you can lay 10 bricks per hour, you can calculate the total time required.
-
Everyday Life: Dividing tasks among family members, sharing food equally, or splitting bills are all everyday examples where division plays a vital role.
Extending the Concept: Division with Remainders
While 1,000 ÷ 10 results in a whole number, not all division problems are so neat. Consider dividing 1,003 by 10. In this case, the answer is 100 with a remainder of 3. Understanding remainders is crucial in many contexts, such as determining leftover materials in construction or handling unequal distribution of resources.
Connecting Division to Other Mathematical Concepts
Division is intrinsically linked to other mathematical concepts:
-
Fractions: The expression 1,000/10 can also be represented as a fraction. Fractions represent parts of a whole and are closely related to division.
-
Decimals: Division can result in decimal answers, particularly when the divisor doesn't divide the dividend evenly. For example, 1,005 ÷ 10 = 100.5.
-
Ratios and Proportions: Ratios compare two quantities, and proportions are equal ratios. Understanding division helps in solving problems involving ratios and proportions.
-
Algebra: Division is a fundamental operation in algebra, used to solve equations and simplify expressions.
Frequently Asked Questions (FAQs)
-
Q: What is the most efficient method to divide 1,000 by 10?
- A: For this specific problem, canceling zeros is the quickest and most intuitive method.
-
Q: Can I use a calculator to solve 1,000 ÷ 10?
- A: Yes, a calculator will readily provide the answer, 100. However, understanding the underlying principles is crucial for problem-solving beyond simple calculations.
-
Q: What if I divide by a number other than 10?
- A: The same principles apply, although the calculation will be different. The method used would depend on the divisor. For larger or more complex numbers, long division becomes more useful.
-
Q: What is the significance of understanding division beyond simply getting the answer?
- A: Understanding division allows you to solve a wide range of real-world problems, to think critically, and to build a strong foundation for more advanced mathematical concepts. It's not just about getting the answer; it's about comprehending the process and its implications.
Conclusion: More Than Just an Answer
This in-depth exploration of 1,000 divided by 10 demonstrates that even seemingly simple arithmetic problems can reveal profound mathematical insights. While the answer, 100, is straightforward, the underlying principles and real-world applications are far-reaching. Mastering division is not just about memorizing procedures; it's about developing a deep understanding of how this fundamental operation shapes our understanding of quantity, proportion, and the world around us. This knowledge extends far beyond the classroom and empowers you to tackle more complex problems with confidence and clarity. The simplicity of 1,000 divided by 10 serves as a gateway to a much richer understanding of mathematics and its practical applications.
Latest Posts
Latest Posts
-
Positive Words Starting With A
Sep 16, 2025
-
Convert 225 Fahrenheit To Celsius
Sep 16, 2025
-
Quiz With Multiple Choice Answers
Sep 16, 2025
-
Words With The Prefix Re
Sep 16, 2025
-
How Do You Sow Seeds
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 000 Divided By 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.