15 20 As A Percentage
candidatos
Sep 20, 2025 · 5 min read
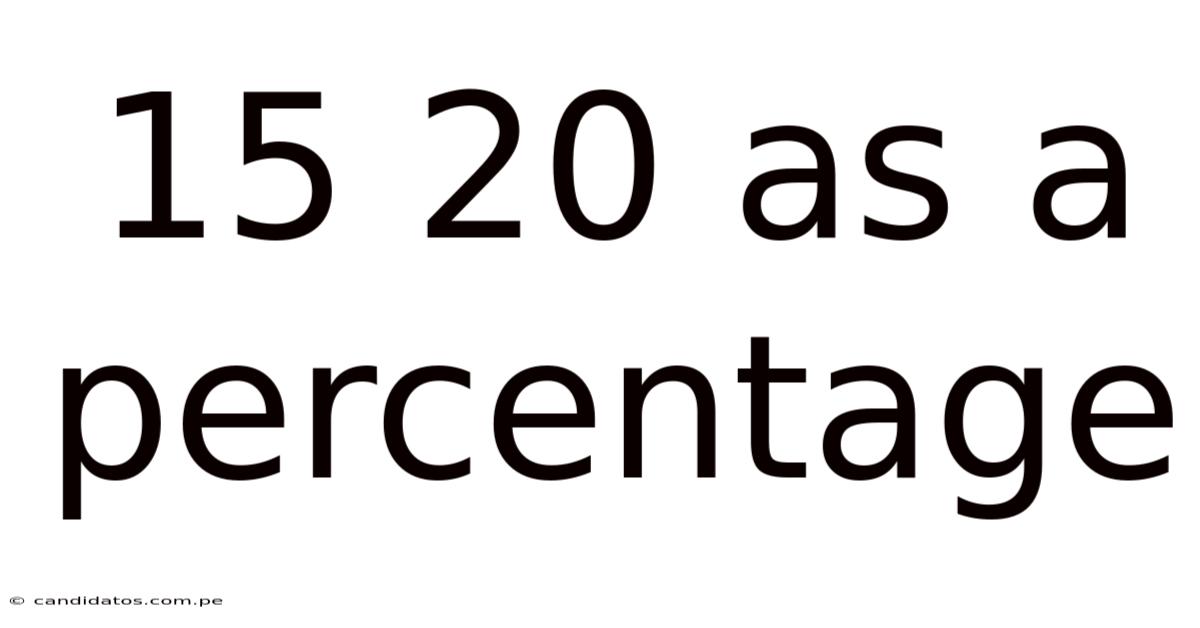
Table of Contents
Decoding the Percentage: Understanding 15 of 20 as a Percentage
Calculating percentages is a fundamental skill applicable across various aspects of life, from academic pursuits to financial planning and everyday decision-making. Understanding how to express a part of a whole as a percentage is crucial for interpreting data, comparing values, and making informed judgments. This article delves into the specific calculation of 15 out of 20 as a percentage, providing a step-by-step guide, exploring the underlying mathematical principles, and offering practical applications to solidify your understanding. We'll also tackle common misconceptions and provide you with the tools to confidently calculate any fraction as a percentage.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the calculation of 15 out of 20 as a percentage, let's refresh our understanding of the interconnectedness of fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For instance, 15/20 signifies 15 parts out of a total of 20 parts.
-
Decimal: A decimal is a representation of a number using a base-ten system, with a decimal point separating the whole number part from the fractional part. Decimals are often used interchangeably with fractions, offering an alternative way of expressing the same value.
-
Percentage: A percentage is a way of expressing a fraction or decimal as a proportion of 100. The percentage symbol (%) indicates that the number represents a fraction of 100. For example, 75% means 75 out of 100, or 75/100.
Calculating 15 out of 20 as a Percentage: A Step-by-Step Guide
To calculate 15 out of 20 as a percentage, we follow these simple steps:
Step 1: Express the values as a fraction.
The given information, "15 out of 20," is directly expressed as a fraction: 15/20.
Step 2: Convert the fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator (15) by the denominator (20):
15 ÷ 20 = 0.75
Step 3: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.75 x 100 = 75%
Therefore, 15 out of 20 is equal to 75%.
Mathematical Explanation: The Underlying Principles
The conversion from a fraction to a percentage involves a fundamental mathematical concept: proportionality. A percentage represents a proportion relative to 100. The process of converting a fraction to a percentage essentially scales the fraction to a denominator of 100.
In our example, 15/20 is equivalent to finding a fraction with a denominator of 100 that represents the same proportion. We can achieve this by finding an equivalent fraction:
We can simplify the fraction 15/20 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 5:
15 ÷ 5 = 3 20 ÷ 5 = 4
This simplifies the fraction to 3/4. To convert this to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and denominator by 25:
3 x 25 = 75 4 x 25 = 100
This gives us the equivalent fraction 75/100, which is directly represented as 75%. This demonstrates the underlying principle of proportionality – maintaining the same ratio while scaling to a different denominator.
Practical Applications: Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios:
-
Academic Performance: If a student answers 15 out of 20 questions correctly on a test, their score is 75%. This allows for easy comparison of performance across different tests or assignments.
-
Sales and Discounts: A store offering a 75% discount on an item means the price is reduced by three-quarters of its original value. Understanding percentages is essential for calculating the final price after a discount.
-
Financial Calculations: Interest rates, loan repayments, and investment returns are often expressed as percentages. Calculating percentages helps us make informed financial decisions.
-
Data Analysis: Many statistical analyses involve calculating percentages to represent proportions within a dataset. This aids in visualizing and interpreting data effectively.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of ingredients in a recipe, or understanding tax rates all involve percentage calculations.
Common Misconceptions and Pitfalls
Several common misconceptions can lead to errors in percentage calculations:
-
Confusing numerator and denominator: Always ensure you correctly identify the part (numerator) and the whole (denominator) when setting up the fraction.
-
Incorrect decimal-to-percentage conversion: Remember to multiply the decimal by 100, not just move the decimal point.
-
Ignoring simplification: Simplifying the fraction before converting to a decimal can make the calculation easier.
-
Overlooking the context: Ensure you understand the context of the percentage calculation; a 75% score on a test is different from a 75% discount.
Frequently Asked Questions (FAQ)
Q1: How can I calculate other fractions as percentages?
A: Follow the same three-step process: Convert the fraction to a decimal by dividing the numerator by the denominator, then multiply the decimal by 100 and add the percentage symbol.
Q2: What if the fraction doesn't simplify easily?
A: You can still divide the numerator by the denominator to get a decimal, then convert the decimal to a percentage. A calculator can be helpful for more complex fractions.
Q3: Are there any online tools or calculators for calculating percentages?
A: Yes, many online calculators are available that can perform percentage calculations quickly and accurately. However, understanding the underlying process is crucial for problem-solving and avoiding errors.
Q4: Can I express a percentage as a fraction or a decimal?
A: Absolutely! A percentage can always be converted back into a fraction by placing the percentage value over 100 and simplifying, or into a decimal by dividing the percentage value by 100.
Conclusion: Mastering Percentage Calculations
Calculating 15 out of 20 as a percentage, resulting in 75%, is a straightforward process that demonstrates the fundamental principles of fractions, decimals, and percentages. Understanding these concepts and the step-by-step procedure allows you to tackle various percentage calculations confidently. This knowledge is a valuable tool for navigating numerous aspects of daily life, from academic pursuits to financial management and data analysis. By understanding the underlying mathematical principles and practicing these calculations, you'll develop a strong foundation for successfully applying percentage calculations in various situations. Remember, the key is to practice consistently and to always double-check your work to ensure accuracy.
Latest Posts
Latest Posts
-
Difference Between Proprietorship And Partnership
Sep 20, 2025
-
How To Find Yield Load
Sep 20, 2025
-
3 5 As An Equivalent Fraction
Sep 20, 2025
-
Things That Rhyme With Show
Sep 20, 2025
-
5 Letter Words Beginning Pa
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 15 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.