3/5 As An Equivalent Fraction
candidatos
Sep 20, 2025 · 6 min read
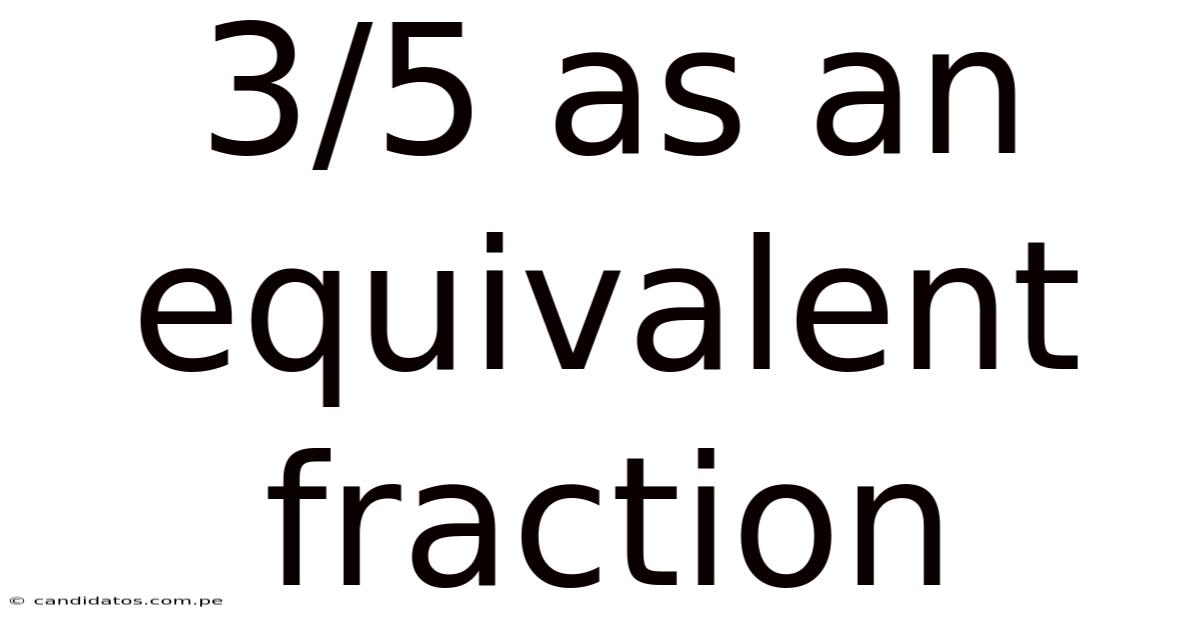
Table of Contents
Understanding 3/5: Exploring Equivalent Fractions and Their Applications
Fractions are fundamental building blocks in mathematics, representing parts of a whole. Understanding fractions, especially how to find equivalent fractions, is crucial for mastering more advanced mathematical concepts. This article delves deep into the fraction 3/5, exploring its equivalent fractions, demonstrating how to find them, and showcasing their practical applications in various fields. We'll uncover why understanding equivalent fractions is so important and how this knowledge can empower you to solve a wide range of problems. This comprehensive guide will leave you with a solid understanding of 3/5 and its equivalents, ready to tackle fraction-based challenges with confidence.
What is 3/5? A Deep Dive into the Fraction
The fraction 3/5 represents three parts out of a total of five equal parts. The number 3 is the numerator, indicating the number of parts we are considering. The number 5 is the denominator, representing the total number of equal parts that make up the whole. Imagine a pizza cut into five equal slices. If you eat three slices, you have consumed 3/5 of the pizza. This simple example illustrates the core concept of fractions and how they represent proportions.
Finding Equivalent Fractions of 3/5: The Fundamental Principle
Equivalent fractions represent the same proportion or value, even though they look different. The key principle behind finding equivalent fractions is to multiply (or divide) both the numerator and the denominator by the same non-zero number. This ensures that the ratio between the numerator and denominator remains constant, thus preserving the original value of the fraction.
Let's find some equivalent fractions of 3/5:
- Multiplying by 2: (3 x 2) / (5 x 2) = 6/10. This means 3/5 is equivalent to 6/10.
- Multiplying by 3: (3 x 3) / (5 x 3) = 9/15. Therefore, 3/5 is also equivalent to 9/15.
- Multiplying by 4: (3 x 4) / (5 x 4) = 12/20. Similarly, 3/5 equals 12/20.
- Multiplying by 5: (3 x 5) / (5 x 5) = 15/25. We see that 3/5 is equivalent to 15/25.
- Multiplying by 10: (3 x 10) / (5 x 10) = 30/50. Thus, 3/5 is equal to 30/50.
And so on. We can generate an infinite number of equivalent fractions for 3/5 simply by multiplying both the numerator and the denominator by any whole number greater than zero.
Simplifying Fractions: Finding the Simplest Form
While we can create countless equivalent fractions, it's often beneficial to work with the simplest form of a fraction. This is the fraction where the numerator and denominator have no common factors other than 1. This process is called simplifying or reducing a fraction.
To simplify a fraction, we find the greatest common divisor (GCD) or highest common factor (HCF) of the numerator and denominator and divide both by this GCD.
For example, let's simplify the fraction 15/25:
The GCD of 15 and 25 is 5. Dividing both the numerator and denominator by 5, we get:
15/5 ÷ 25/5 = 3/5
This confirms that 15/25 is an equivalent fraction of 3/5, and 3/5 is the simplest form of the fraction.
Visualizing Equivalent Fractions
Visual aids can greatly enhance understanding. Imagine a rectangular bar divided into five equal parts. Shading three of these parts represents 3/5. Now, imagine dividing each of these five parts into two equal parts. You now have ten equal parts, and six of them are shaded (representing 6/10). The area covered remains the same, visually demonstrating that 3/5 and 6/10 are equivalent. This visual representation reinforces the concept of equivalent fractions.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions isn't just a theoretical exercise; it has wide-ranging practical applications:
-
Baking and Cooking: Recipes often require fractional measurements. Understanding equivalent fractions allows for flexibility; you can easily convert a recipe that calls for 3/5 of a cup of flour to an equivalent amount like 6/10 or 9/15 of a cup.
-
Measurement and Scale: Maps and blueprints use scales that rely on ratios and fractions. Converting between different scales often involves working with equivalent fractions.
-
Finance and Budgeting: Managing finances involves working with percentages and proportions, which are fundamentally based on fractions. Understanding equivalent fractions facilitates calculations and comparisons.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Equivalent fractions help in converting units and ensuring accuracy.
-
Data Analysis and Statistics: Presenting data often involves using fractions and percentages. Understanding equivalent fractions helps in interpreting and comparing data effectively.
Working with Equivalent Fractions: Common Mistakes to Avoid
While seemingly straightforward, working with equivalent fractions can lead to common mistakes. Here are some pitfalls to avoid:
-
Incorrectly multiplying or dividing: Remember that you must multiply or divide both the numerator and the denominator by the same number. Multiplying only the numerator or denominator will change the value of the fraction.
-
Forgetting to simplify: Always simplify your answer to its simplest form to ensure clarity and efficiency.
-
Confusing equivalent fractions with addition or subtraction: Remember that finding equivalent fractions involves multiplication or division, not addition or subtraction.
Frequently Asked Questions (FAQ)
Q: Are there any limitations to finding equivalent fractions?
A: The only limitation is that you cannot divide by zero. Both the numerator and denominator must be divided by a non-zero number to maintain the value of the fraction.
Q: Why is it important to learn about equivalent fractions?
A: Understanding equivalent fractions is essential for mastering more complex mathematical concepts like addition, subtraction, multiplication, and division of fractions, as well as working with decimals and percentages.
Q: How can I check if two fractions are equivalent?
A: You can check if two fractions are equivalent by simplifying both to their simplest forms. If the simplified forms are identical, then the original fractions are equivalent. Alternatively, you can cross-multiply: if the product of the numerator of one fraction and the denominator of the other is equal to the product of the numerator of the other fraction and the denominator of the first, then the fractions are equivalent.
Q: Can I use decimals to represent equivalent fractions?
A: Yes, you can convert a fraction to its decimal equivalent by dividing the numerator by the denominator. For example, 3/5 = 0.6. Equivalent fractions will have the same decimal representation.
Conclusion: Mastering the Art of Equivalent Fractions
Understanding the concept of equivalent fractions, particularly with a fraction like 3/5, is a cornerstone of mathematical proficiency. From its fundamental principles to its widespread practical applications, the ability to identify and work with equivalent fractions is invaluable. This article provided a comprehensive exploration of 3/5 and its numerous equivalent fractions, emphasizing the importance of simplifying fractions to their lowest terms and highlighting the potential pitfalls to avoid. By mastering this fundamental concept, you build a strong foundation for more advanced mathematical pursuits and equip yourself with the problem-solving skills necessary to navigate numerous real-world scenarios. Remember to practice regularly, and soon you’ll find yourself confidently tackling any fraction-based challenge.
Latest Posts
Latest Posts
-
Conductor We Have A Problem
Sep 20, 2025
-
Physics Year 12 Formula Sheet
Sep 20, 2025
-
Definition Of Prim And Proper
Sep 20, 2025
-
Put Fractions In Order Worksheet
Sep 20, 2025
-
155cm To Inches And Feet
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3/5 As An Equivalent Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.