5 X 4 X 3
candidatos
Sep 18, 2025 · 6 min read
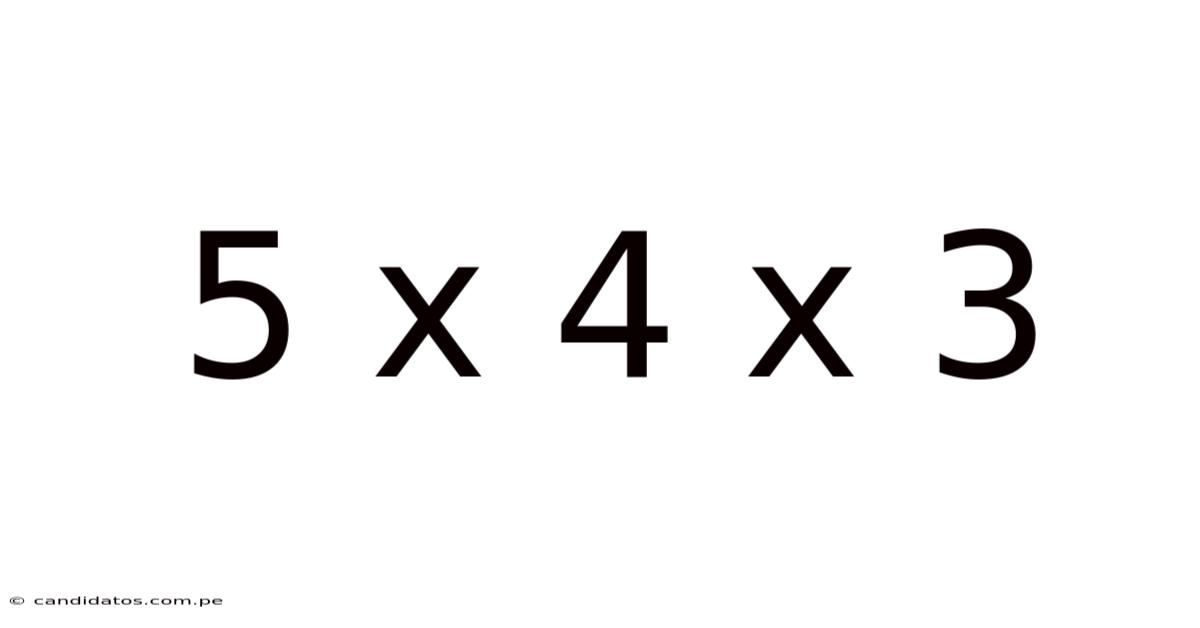
Table of Contents
Unlocking the Mysteries of 5 x 4 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical expression "5 x 4 x 3," delving beyond the immediate answer to uncover the underlying principles of multiplication, its practical applications, and its connection to broader mathematical concepts. Understanding this seemingly basic equation provides a foundation for grasping more complex mathematical ideas and problem-solving skills. We will examine the calculation itself, explore different methods of solving it, discuss its relevance in various fields, and address frequently asked questions. This comprehensive guide is designed for learners of all levels, from elementary school students to those seeking a refresher on fundamental mathematical concepts.
Understanding the Basics: Multiplication as Repeated Addition
At its core, multiplication is a shortcut for repeated addition. The expression "5 x 4 x 3" can be interpreted as:
-
5 added to itself 4 times, and then the result multiplied by 3. This translates to (5 + 5 + 5 + 5) x 3 = 20 x 3 = 60.
-
Alternatively, it can be seen as 5 groups of 4, each group then multiplied by 3. This could be visualized as 5 rows of 4 items, and then having 3 sets of this arrangement.
This understanding of multiplication as repeated addition is crucial for building a strong foundation in mathematics. It helps visualize the operation and makes it less abstract, particularly for younger learners.
Methods for Solving 5 x 4 x 3
While the simplest approach is to solve the equation step-by-step (as shown above), there are other methods, highlighting the flexibility and properties of multiplication:
-
Order of Operations: Multiplication is commutative, meaning the order of the numbers doesn't affect the result. We can rearrange the equation to simplify the calculation:
- Method 1: (5 x 4) x 3 = 20 x 3 = 60
- Method 2: (5 x 3) x 4 = 15 x 4 = 60
- Method 3: (4 x 3) x 5 = 12 x 5 = 60
This demonstrates the associative property of multiplication, where the grouping of numbers doesn't alter the final product. This flexibility is extremely useful when dealing with larger numbers or more complex equations.
-
Distributive Property: While less intuitive for this particular equation, the distributive property can be applied when dealing with more complex expressions involving addition or subtraction. For example, if we had 5 x (4 + 3), we would distribute the 5 to both 4 and 3, resulting in (5 x 4) + (5 x 3) = 20 + 15 = 35.
-
Mental Math Techniques: With practice, solving 5 x 4 x 3 mentally becomes straightforward. Many people develop their own shortcuts and strategies, often involving breaking down the numbers into easier-to-manage components. For instance, recognizing that 5 x 4 is 20 makes the subsequent multiplication by 3 much simpler.
Real-World Applications: Where 5 x 4 x 3 Shows Up
The seemingly simple calculation 5 x 4 x 3 has surprisingly broad applications in various real-world scenarios:
-
Everyday Calculations: Imagine you're buying 5 packs of cookies, each containing 4 rows of 3 cookies. To find the total number of cookies, you'd perform 5 x 4 x 3. This demonstrates the practicality of multiplication in everyday shopping and inventory management.
-
Geometry and Volume: Consider a rectangular prism (a box) with dimensions of 5 cm, 4 cm, and 3 cm. The volume of the prism is calculated by multiplying these dimensions: 5 x 4 x 3 = 60 cubic centimeters. This highlights the use of multiplication in spatial reasoning and geometric calculations.
-
Data Analysis: In data analysis, multiplication is often used to scale data or perform calculations involving multiple variables. For example, if you have 5 groups of data, each with 4 subgroups, and each subgroup containing 3 data points, the total number of data points would be 5 x 4 x 3.
-
Engineering and Construction: In engineering and construction, multiplication is crucial for calculating material requirements, project timelines, and cost estimations. Understanding the relationship between quantities and dimensions allows for accurate planning and efficient resource allocation.
-
Finance and Budgeting: Multiplication is fundamental for financial calculations, such as calculating interest, determining investment returns, or projecting future earnings. Understanding how multiplication works is essential for managing personal finances and making informed financial decisions.
Expanding the Concept: Beyond the Basics
While seemingly simple, 5 x 4 x 3 offers a gateway to explore deeper mathematical concepts:
-
Factors and Multiples: The numbers 5, 4, and 3 are factors of 60. Conversely, 60 is a multiple of 5, 4, and 3. Understanding factors and multiples is crucial for simplifying fractions, finding common denominators, and working with prime numbers.
-
Prime Factorization: Breaking down a number into its prime factors (numbers divisible only by 1 and themselves) is a fundamental concept in number theory. While 5 is a prime number, 4 (2 x 2) and 3 are also prime numbers, demonstrating the prime factorization of 60 as 2 x 2 x 3 x 5.
-
Exponents and Powers: Extending this concept, we can see how multiplication relates to exponents. For example, 2² (2 squared or 2 to the power of 2) is 2 x 2 = 4. This lays the groundwork for understanding exponential growth and decay, crucial in various fields, from finance to biology.
Frequently Asked Questions (FAQ)
-
Q: What is the quickest way to solve 5 x 4 x 3?
- A: The quickest way depends on individual preference and familiarity with multiplication tables. Most people find (5 x 4) x 3 or (5 x 3) x 4 the most efficient.
-
Q: Can I use a calculator to solve 5 x 4 x 3?
- A: Yes, calculators are useful tools, especially for more complex calculations. However, understanding the underlying principles of multiplication is crucial for developing mathematical fluency.
-
Q: Is there a difference between 5 x 4 x 3 and 3 x 4 x 5?
- A: No, due to the commutative and associative properties of multiplication, the order of the numbers doesn't affect the final result. Both expressions equal 60.
-
Q: How can I help my child understand 5 x 4 x 3?
- A: Use visual aids like counters, blocks, or drawings to represent the equation as repeated addition or groups of items. Make it relatable to real-world scenarios to enhance comprehension.
Conclusion: The Enduring Significance of 5 x 4 x 3
While seemingly a simple equation, "5 x 4 x 3" serves as a powerful illustration of fundamental mathematical principles. It underscores the importance of understanding multiplication as repeated addition, demonstrates the associative and commutative properties, and showcases its widespread applications in various fields. Mastering this basic calculation builds a solid foundation for tackling more complex mathematical problems and fostering a deeper appreciation for the power of mathematics in our everyday lives. By exploring this seemingly simple equation, we've unveiled a world of mathematical possibilities, highlighting the interconnectedness of fundamental concepts and their relevance to our understanding of the world around us. The journey from a simple multiplication problem to a deeper understanding of mathematical principles is a testament to the power of curiosity and the beauty of mathematics itself.
Latest Posts
Latest Posts
-
The Horse And His Boy
Sep 18, 2025
-
Alice In Wonderland Blue Dress
Sep 18, 2025
-
Maths Worksheet For Class 1
Sep 18, 2025
-
180 Australian Dollars In Euro
Sep 18, 2025
-
Boiling Point Of Hydrogen Fluoride
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 X 4 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.