Y 1 X 1 X
candidatos
Sep 16, 2025 · 5 min read
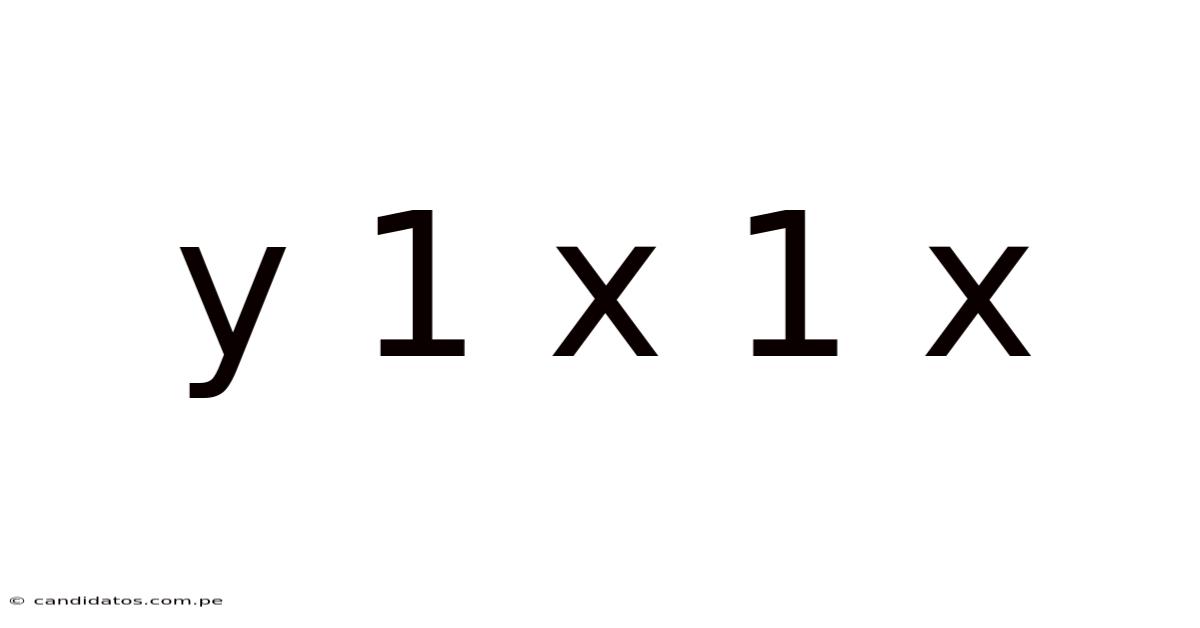
Table of Contents
Decoding Y = 1x¹: A Deep Dive into Linear Equations and Their Applications
This article explores the seemingly simple equation, Y = 1x¹, delving into its fundamental mathematical principles, real-world applications, and the broader context of linear equations. Understanding this basic equation is crucial for grasping more complex mathematical concepts and their applications in various fields. We'll break down the components, explore its graphical representation, and examine its uses in diverse areas like physics, economics, and computer science.
Understanding the Basics: Components of Y = 1x¹
At first glance, Y = 1x¹ appears deceptively simple. Let's dissect each component:
-
Y: This represents the dependent variable. Its value depends on the value of x. Think of Y as the output or result.
-
1: This is the slope or gradient of the line. It indicates the rate of change of Y with respect to x. A slope of 1 means that for every one-unit increase in x, Y increases by one unit.
-
x: This is the independent variable. Its value is chosen independently and determines the value of Y. Think of x as the input.
-
¹: This is the exponent, indicating that x is raised to the power of 1. This signifies a linear relationship between x and Y – meaning the graph of this equation will be a straight line.
Graphical Representation: Visualizing the Linear Relationship
The equation Y = 1x¹ represents a straight line on a Cartesian coordinate system (x-y plane). The slope of 1 means the line has a positive inclination, rising from left to right. The line passes through the origin (0,0) because when x = 0, Y = 0.
To visualize this, imagine plotting several points:
- If x = 1, Y = 1 (point (1,1))
- If x = 2, Y = 2 (point (2,2))
- If x = 3, Y = 3 (point (3,3))
- If x = -1, Y = -1 (point (-1,-1))
- If x = -2, Y = -2 (point (-2,-2))
Connecting these points reveals a straight line with a slope of 1, passing through the origin. This visual representation clearly demonstrates the direct proportional relationship between x and Y: as x increases, Y increases proportionally.
Beyond the Basics: Expanding the Concept
While Y = 1x¹ appears simple, it forms the bedrock for understanding more complex linear equations. The general form of a linear equation is Y = mx + c, where:
- m represents the slope (the rate of change of Y with respect to x). In our original equation, m = 1.
- c represents the y-intercept (the point where the line intersects the y-axis). In Y = 1x¹, c = 0, meaning the line passes through the origin.
Understanding the variables m and c allows us to model a vast array of real-world scenarios. For instance:
- A positive slope (m > 0): Indicates a positive relationship – as x increases, Y increases.
- A negative slope (m < 0): Indicates a negative relationship – as x increases, Y decreases.
- A zero slope (m = 0): Indicates a horizontal line, where Y remains constant regardless of the value of x.
- A non-zero y-intercept (c ≠ 0): Indicates that the line does not pass through the origin.
Real-World Applications: Where Linear Equations Shine
Linear equations, even the simplest like Y = 1x¹, have far-reaching applications in numerous fields:
-
Physics: Calculating distance traveled at a constant speed. If speed (x) is constant, then distance (Y) is directly proportional to time.
-
Economics: Modeling supply and demand. A simple linear equation can represent the relationship between the price of a good (x) and the quantity demanded (Y).
-
Computer Science: In algorithms and data structures, linear equations are used extensively in calculations and representations. Linear search, a fundamental algorithm, relies on a linear relationship between the input and the number of steps required.
-
Engineering: Linear equations are essential in structural analysis, calculating forces and stresses in various structures.
-
Finance: Calculating simple interest. The interest earned (Y) is directly proportional to the principal amount (x) and the interest rate (m) over a given time period.
-
Biology: Modeling population growth under ideal conditions. In simplified models, population size (Y) can be linearly related to time (x) under specific circumstances.
Solving Linear Equations: Techniques and Methods
Solving for either x or Y in a linear equation is relatively straightforward. For Y = 1x¹, if we know the value of x, we simply substitute it into the equation to find Y. Similarly, if we know the value of Y, we solve for x by dividing Y by 1 (which is simply Y).
Advanced Concepts: Extending the Linear Model
While Y = 1x¹ illustrates the simplest form, understanding this foundation lays the groundwork for tackling more sophisticated linear models:
-
Multiple Linear Regression: Extends the concept to include multiple independent variables influencing the dependent variable. For instance, Y = m₁x₁ + m₂x₂ + c, where x₁ and x₂ are independent variables with respective slopes m₁ and m₂.
-
Linear Programming: A powerful optimization technique used to find the best outcome (maximum or minimum) given a set of linear constraints.
-
Systems of Linear Equations: Involves solving multiple linear equations simultaneously to find the values of multiple variables.
Frequently Asked Questions (FAQ)
Q: What if the slope in Y = mx + c isn't 1?
A: A different slope simply means the line is steeper or less steep. A slope of 2 means Y increases twice as fast as x. A slope of 0.5 means Y increases half as fast as x. A negative slope means Y decreases as x increases.
Q: What is the significance of the y-intercept?
A: The y-intercept represents the value of Y when x is 0. It's the point where the line crosses the y-axis. In many real-world scenarios, the y-intercept can represent an initial value or a starting point.
Q: How can I tell if a relationship is linear?
A: A linear relationship exhibits a constant rate of change between the variables. If you plot the data points and they form a straight line, it's a linear relationship.
Conclusion: The Power of Simplicity
The equation Y = 1x¹ might seem rudimentary, but it's a cornerstone of mathematics and a powerful tool for understanding and modeling various real-world phenomena. By mastering the fundamentals of this equation, you gain a strong foundation for exploring more complex mathematical concepts and their broad applications in science, technology, engineering, and beyond. The simplicity of this equation belies its profound influence and widespread utility in countless areas of study and application. Its understanding unlocks a gateway to a deeper appreciation of the power and elegance of linear relationships.
Latest Posts
Latest Posts
-
Gradient Of A Horizontal Line
Sep 17, 2025
-
Short Sound Of I Words
Sep 17, 2025
-
Why Do Sweat Taste Salty
Sep 17, 2025
-
150 Dollars In Indian Rupees
Sep 17, 2025
-
Baa Baa Black Sheep Words
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Y 1 X 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.