X 2 X X 2
candidatos
Sep 19, 2025 · 6 min read
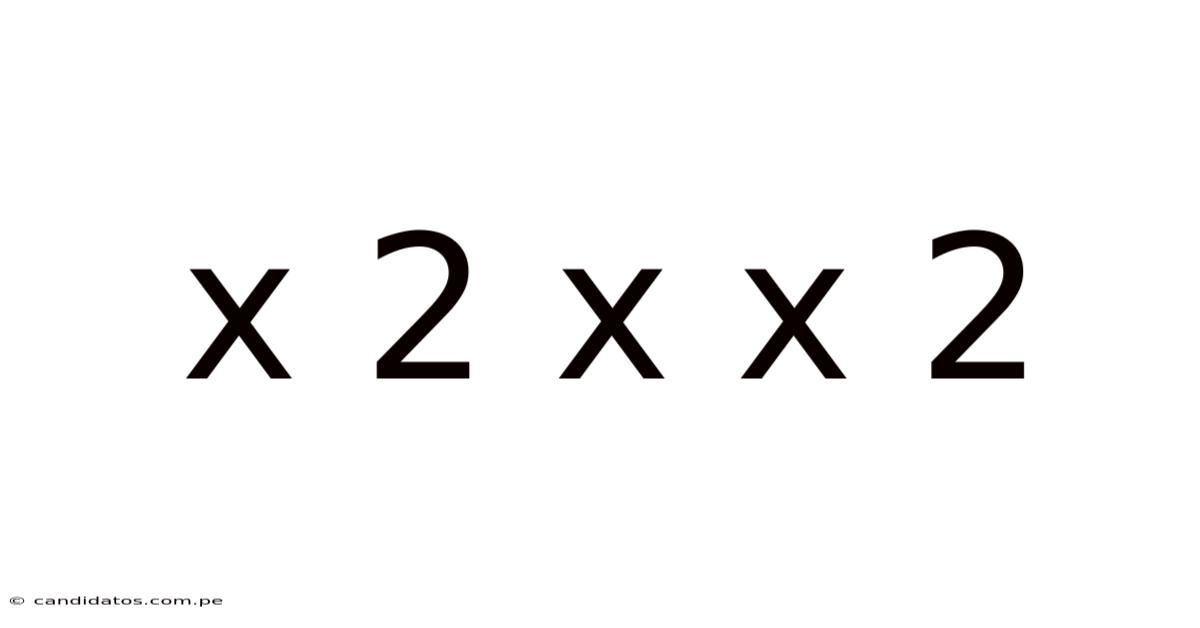
Table of Contents
Decoding the Mystery: A Deep Dive into the Mathematical Expression "x² x x²"
This article explores the mathematical expression "x² x x²," delving into its simplification, applications, and broader implications within algebra and beyond. We'll break down the expression step-by-step, making it accessible to readers of all mathematical backgrounds, from beginners grappling with basic algebraic concepts to those seeking a deeper understanding of exponential notation and its properties. Understanding this seemingly simple expression opens doors to more complex mathematical concepts and problem-solving techniques.
Understanding the Basics: Exponents and Multiplication
Before we tackle the core expression "x² x x²," let's refresh our understanding of two fundamental mathematical concepts: exponents and multiplication.
-
Exponents: An exponent (or power) indicates how many times a base number is multiplied by itself. For example, x² (pronounced "x squared") means x * x. Similarly, x³ (pronounced "x cubed") means x * x * x, and so on. The exponent sits as a superscript to the right of the base number.
-
Multiplication: Multiplication is a fundamental arithmetic operation representing repeated addition. It signifies the combining of quantities. In algebra, the multiplication symbol (×) is often omitted, especially when a variable is multiplied by another variable or a number. For instance, 2x means 2 multiplied by x, and xy means x multiplied by y.
Simplifying "x² x x²"
Now, let's dissect our target expression: x² x x². Remembering that x² means x * x, we can rewrite the expression as:
(x * x) × (x * x)
This illustrates that we are multiplying x by itself a total of four times. Therefore, we can simplify the expression using the rules of exponents:
x² x x² = x⁽²⁺²⁾ = x⁴
This simplification relies on the fundamental rule of exponents: when multiplying terms with the same base, we add their exponents. In this case, the base is 'x,' and the exponents are 2 and 2. Adding them together (2 + 2 = 4) gives us the simplified expression x⁴ (pronounced "x to the power of four" or "x raised to the fourth power").
Practical Applications and Real-World Examples
The simplification of x² x x² = x⁴ might seem abstract, but its applications are widespread across various fields. Here are a few examples:
-
Area Calculation: Imagine a square with sides of length x. The area of this square is x². Now, consider a larger square formed by four of these smaller squares arranged in a 2x2 grid. The area of this larger square is (x²) x 2 x 2 = 4x². This illustrates the concept of area scaling and demonstrates how exponents and multiplication are used to calculate areas in geometric problems. Another example would be if we considered the smaller square as having an area of x², and then we have another identical square next to it. The total area of both would be 2x².
-
Volume Calculation: If we extend the concept to three dimensions, let's consider a cube with sides of length x. Its volume is x³. If we then take two of these cubes, then the total volume will be 2x³. A more complex scenario might involve a larger cube made up of smaller cubes, further highlighting the utility of exponential notation in volumetric calculations.
-
Computer Science: In computer science, particularly in algorithms and data structures, exponential notation is frequently encountered. For instance, the time complexity of an algorithm might be described using exponential functions, where the exponent represents the growth rate of the algorithm with respect to input size. An algorithm that has a time complexity of O(x²) would process data much more efficiently than an algorithm with a complexity of O(x⁴).
-
Physics: Many physical phenomena are modeled using exponential functions. For instance, the intensity of light decreases exponentially with distance from the source. The decay rate is represented by an exponent, reflecting the rate at which the intensity falls off.
Expanding the Concept: More Complex Scenarios
While we've focused on the straightforward simplification of x² x x², let's explore more complex scenarios incorporating similar principles:
-
x³ x x²: Applying the same rule as before, we add the exponents: x³ x x² = x⁽³⁺²⁾ = x⁵.
-
x⁴ x x⁻²: Here, we encounter a negative exponent. Remember that x⁻ⁿ = 1/xⁿ. Therefore: x⁴ x x⁻² = x⁽⁴⁻²⁾ = x².
-
(x²)³: This involves the power of a power. In this case, we multiply the exponents: (x²)³ = x⁽²ˣ³⁾ = x⁶.
-
(2x²) x (3x³): Here, we multiply the coefficients (2 and 3) and add the exponents of the 'x' terms: (2x²) x (3x³) = 6x⁵.
These examples showcase the flexibility and power of exponential notation and the rules governing its manipulation within algebraic expressions. Mastering these rules is fundamental to success in algebra and related mathematical disciplines.
The Importance of Understanding the Fundamentals
The seemingly simple expression "x² x x²" serves as a gateway to a richer understanding of more complex mathematical concepts. Its simplification using exponential rules isn't just about manipulating symbols; it's about grasping the underlying principles that govern the behavior of exponential functions. This understanding is crucial for tackling more advanced topics like calculus, differential equations, and various applications in science and engineering.
Frequently Asked Questions (FAQ)
Q1: What happens if the bases are different?
A: The rule of adding exponents only applies when the bases are the same. If you have an expression like x² x y², you cannot simplify it further. It remains x²y².
Q2: Can I use this simplification in all mathematical contexts?
A: Yes, the simplification of x² x x² = x⁴ holds true in most mathematical contexts. However, it's always important to consider the specific constraints or rules of the context in which you're working. For example, there may be domain restrictions, but this simplification still holds.
Q3: What if there are more terms?
A: If you have more terms with the same base, you simply continue adding the exponents. For example: x² x x³ x x = x⁽²⁺³⁺¹⁾ = x⁶.
Q4: Are there any exceptions to the exponent rules?
A: While the rules are generally consistent, you need to be cautious when dealing with zero and negative exponents, complex numbers, and specific contexts within advanced mathematics. However, the core principles remain relevant.
Conclusion: Beyond the Basics
This in-depth exploration of the seemingly simple expression "x² x x²" reveals its significance in understanding fundamental algebraic principles. By mastering the manipulation of exponents and their implications, we not only simplify expressions but also develop a foundation for tackling more advanced mathematical problems. The ability to seamlessly work with exponential notation is a cornerstone of mathematical literacy and is essential for success in numerous fields requiring quantitative reasoning. This seemingly simple equation serves as a gateway to a deeper and more rewarding understanding of the world around us, demonstrating the power of mathematical principles in describing patterns and phenomena across diverse disciplines. From area calculations to algorithm analysis, this foundational understanding is essential for any aspiring mathematician or scientist. The principles explored here form the building blocks for more complex mathematical concepts, highlighting the importance of mastering fundamental concepts to solve complex problems effectively. The journey of understanding mathematics often starts with simple equations like this one, paving the way for tackling complex challenges with confidence.
Latest Posts
Latest Posts
-
Meaning Of Consolidation In Accounting
Sep 19, 2025
-
3 4 Is Equal To
Sep 19, 2025
-
18 5 As A Decimal
Sep 19, 2025
-
Wage Price Index Vs Cpi
Sep 19, 2025
-
Words That Rhyme With Ten
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about X 2 X X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.