X 2 X 3 2
candidatos
Sep 19, 2025 · 5 min read
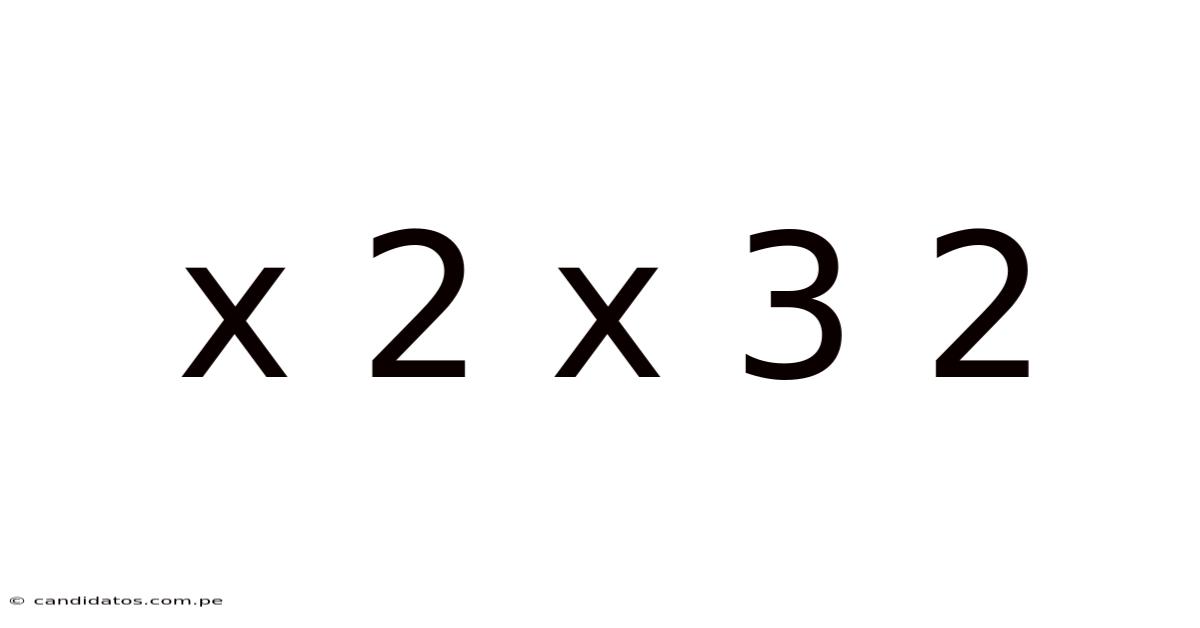
Table of Contents
Decoding the Enigma: A Deep Dive into the Expression "x² x ³ = 2"
This article explores the mathematical expression "x² x ³ = 2," delving into its solution, the underlying principles, and its implications within broader mathematical contexts. We'll examine the different approaches to solving this equation, address potential misconceptions, and explore related concepts to provide a comprehensive understanding. This seemingly simple equation opens doors to a deeper appreciation of algebraic manipulation and exponential properties.
Introduction: Understanding the Problem
The equation x² x ³ = 2 presents a challenge in algebra. At first glance, it might appear straightforward, but understanding the solution requires a solid grasp of exponent rules and algebraic manipulation. The core challenge lies in simplifying the left-hand side of the equation before solving for x. The keyword here is exponent rules, specifically how we handle multiplying terms with the same base but different exponents. This article will guide you through the process step-by-step, explaining the reasoning behind each calculation. We will also explore the nature of the solution and its implications.
Step-by-Step Solution
The key to solving this equation lies in understanding the rules of exponents. When multiplying terms with the same base, we add their exponents. Therefore, x² x ³ can be simplified as follows:
x² x ³ = x⁽²⁺³⁾ = x⁵
This simplifies our original equation to:
x⁵ = 2
Now, we need to isolate x. To do this, we need to find the fifth root of both sides of the equation:
⁵√x⁵ = ⁵√2
This simplifies to:
x = ⁵√2
This is the exact solution. While we can approximate the value of ⁵√2 using a calculator (approximately 1.1487), it's important to remember that x = ⁵√2 is the precise mathematical solution.
Understanding the Fifth Root
The expression ⁵√2 represents the fifth root of 2. This means, what number, when multiplied by itself five times, equals 2? This concept is crucial in understanding the solution. It illustrates the inverse operation of raising a number to the power of 5. Just as squaring a number (raising it to the power of 2) and taking the square root are inverse operations, raising a number to the power of 5 and taking the fifth root are also inverse operations.
Expanding the Concept: Generalization and Applications
The principles used to solve x² x ³ = 2 are applicable to a wide range of similar problems. The general form is:
xᵃ xᵇ = c
Where a and b are exponents, and c is a constant. The solution follows the same pattern:
x⁽ᵃ⁺ᵇ⁾ = c
x = ⁽ᵃ⁺ᵇ⁾√c
This illustrates the power of generalization in mathematics. Understanding the fundamental principles allows us to tackle a broader class of problems, not just the specific case presented initially. This simple equation forms a foundational element in various advanced mathematical concepts.
Exploring Related Concepts
This equation touches upon several crucial mathematical concepts, including:
-
Exponents and Exponential Functions: The equation highlights the importance of understanding exponent rules. Mastering these rules is crucial for tackling more complex problems involving exponential growth and decay, often seen in fields like finance, physics, and biology.
-
Roots and Radicals: The solution involves finding the fifth root, a type of radical expression. Understanding radicals is crucial for solving various algebraic equations and working with functions that involve fractional exponents.
-
Solving Equations: The process of isolating x demonstrates a fundamental skill in algebra: manipulating equations to solve for an unknown variable. This skill is essential for success in all areas of mathematics and its applications.
-
Numerical Approximation: While the exact solution is ⁵√2, we can approximate its value using a calculator. This highlights the interplay between precise mathematical solutions and practical numerical approximations.
Addressing Potential Misconceptions
A common mistake when encountering this type of problem is incorrectly multiplying the exponents instead of adding them. Remember, when multiplying terms with the same base, we add the exponents, not multiply them. This is a crucial distinction in understanding exponent rules.
Another potential issue might involve difficulties in interpreting the fifth root. While not as familiar as the square root, the fifth root represents the inverse operation of raising to the power of 5. Understanding this inverse relationship is essential for correctly solving the equation.
Frequently Asked Questions (FAQ)
-
Q: Can this equation be solved without using exponent rules? A: No. The fundamental process of simplifying x² x ³ requires the application of exponent rules. There is no alternative method that avoids this core principle.
-
Q: Is there more than one solution to this equation? A: For real numbers, there's only one real solution: ⁵√2. However, in the complex number system, there are four additional complex solutions. This expands the problem into the realm of complex analysis.
-
Q: How can I check if my solution is correct? A: Substitute the value of x (⁵√2) back into the original equation: (⁵√2)² x (⁵√2)³ = 2. If the equation holds true, your solution is correct. Remember you can use a calculator to obtain a decimal approximation to check the result.
Conclusion: Beyond the Equation
The seemingly simple equation x² x ³ = 2 serves as a gateway to a deeper understanding of fundamental mathematical concepts. From mastering exponent rules and working with radicals to solving equations and appreciating numerical approximations, this single problem encapsulates several essential skills and knowledge areas within algebra. By carefully dissecting the solution process and understanding its underlying principles, we gain a stronger foundation for tackling more complex mathematical challenges in the future. The journey from a simple equation to an appreciation of its broader mathematical context highlights the power and beauty of mathematical exploration. The ability to generalize the approach to similar problems further underscores the importance of understanding the fundamental principles involved. This deep dive into "x² x ³ = 2" provides not just a solution, but a pathway to a more profound understanding of algebra and its wider applications.
Latest Posts
Latest Posts
-
1 Litre How Many Grams
Sep 19, 2025
-
Tiny Things Studied By Chemists
Sep 19, 2025
-
Diagram Of Wastewater Treatment Plant
Sep 19, 2025
-
Picture Of A Synovial Joint
Sep 19, 2025
-
How To Clean The Womb
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.