X 2 6x 6 0
candidatos
Sep 15, 2025 · 5 min read
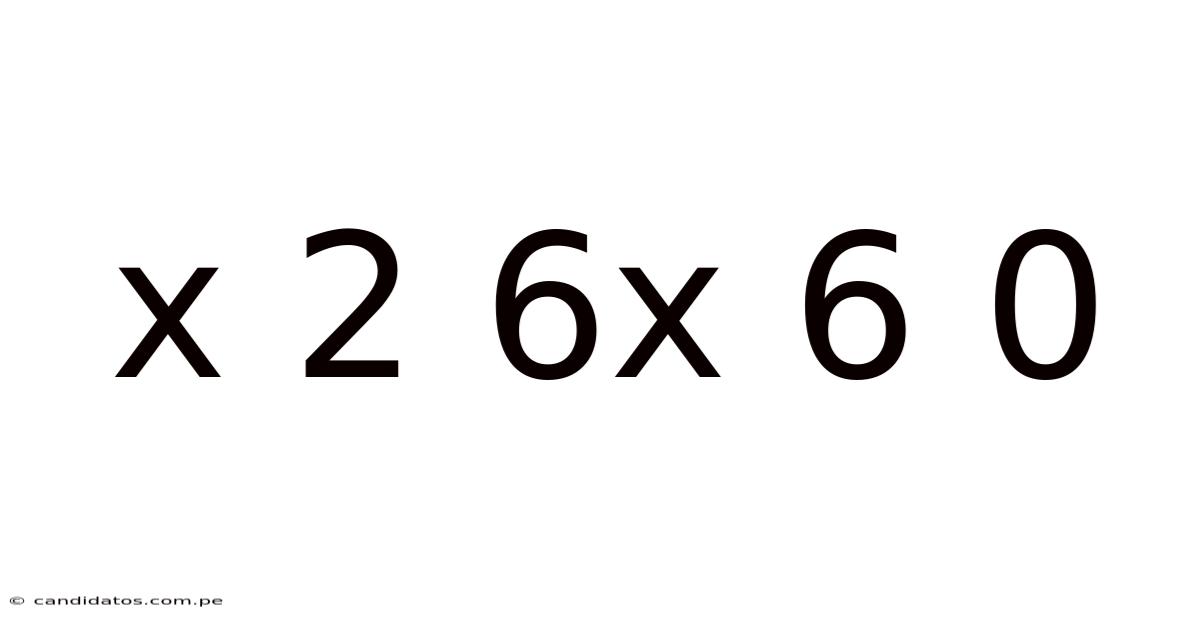
Table of Contents
Decoding the Mystery: Exploring the Mathematical Significance of "x² + 6x + 6 = 0"
This article delves into the mathematical intricacies of the quadratic equation x² + 6x + 6 = 0. We'll explore various methods for solving this equation, delve into the underlying concepts of quadratic equations, and examine its practical applications. Understanding this seemingly simple equation unlocks a deeper understanding of algebra and its role in numerous fields.
Introduction: Understanding Quadratic Equations
A quadratic equation is a second-degree polynomial equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our focus, x² + 6x + 6 = 0, fits this mold perfectly, with a = 1, b = 6, and c = 6. These equations are fundamental in mathematics and have wide-ranging applications in physics, engineering, economics, and computer science. Solving them unlocks the ability to model and solve problems involving parabolic trajectories, optimal resource allocation, and many other real-world scenarios.
Methods for Solving x² + 6x + 6 = 0
There are several established methods for solving quadratic equations. Let's explore the most common approaches applied to our specific equation:
1. The Quadratic Formula: This is a universal method applicable to all quadratic equations. The formula is derived from completing the square and provides a direct solution:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in our values (a = 1, b = 6, c = 6), we get:
x = [-6 ± √(6² - 4 * 1 * 6)] / 2 * 1
x = [-6 ± √(36 - 24)] / 2
x = [-6 ± √12] / 2
x = [-6 ± 2√3] / 2
x = -3 ± √3
Therefore, the two solutions are x = -3 + √3 and x = -3 - √3. These are the exact solutions, expressed in radical form. Approximating these values, we find:
x ≈ -1.268 and x ≈ -4.732
2. Completing the Square: This method involves manipulating the equation to create a perfect square trinomial. Let's see how it works:
x² + 6x + 6 = 0
First, move the constant term to the right side:
x² + 6x = -6
Next, take half of the coefficient of 'x' (which is 6), square it (3² = 9), and add it to both sides:
x² + 6x + 9 = -6 + 9
x² + 6x + 9 = 3
Now, the left side is a perfect square trinomial:
(x + 3)² = 3
Taking the square root of both sides:
x + 3 = ±√3
Solving for x:
x = -3 ± √3
This yields the same solutions as the quadratic formula, confirming its accuracy.
3. Graphing: While not as precise as the algebraic methods, graphing the quadratic function y = x² + 6x + 6 can provide a visual representation of the solutions. The x-intercepts of the graph represent the roots (solutions) of the equation. The parabola will intersect the x-axis at two points, corresponding to the approximate values we calculated earlier.
The Discriminant and the Nature of Roots
The expression b² - 4ac within the quadratic formula is called the discriminant. It determines the nature of the roots of the quadratic equation:
- b² - 4ac > 0: The equation has two distinct real roots (as in our case).
- b² - 4ac = 0: The equation has one real root (a repeated root).
- b² - 4ac < 0: The equation has two complex roots (involving imaginary numbers).
In our equation, the discriminant is 12 (36 - 24 = 12), which is greater than 0, indicating two distinct real roots.
Understanding the Solutions in Context
The solutions x ≈ -1.268 and x ≈ -4.732 are not just abstract numbers; they represent the points where the parabola represented by the equation intersects the x-axis. These points are crucial in various applications. For instance, in physics, they might represent the time it takes for a projectile to hit the ground, or in engineering, the points where a curve intersects a horizontal line.
Practical Applications of Quadratic Equations
The seemingly simple equation x² + 6x + 6 = 0, and quadratic equations in general, have extensive applications across numerous fields:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity, and analyzing oscillatory systems.
- Engineering: Designing bridges, buildings, and other structures; optimizing designs for strength and efficiency; analyzing electrical circuits.
- Economics: Modeling supply and demand curves, determining optimal production levels, and analyzing market equilibrium.
- Computer Science: Used in algorithms for optimization, image processing, and computer graphics.
- Finance: Calculating compound interest, modeling investment growth, and pricing options.
Expanding on the Concept: Beyond the Specific Equation
While we focused on x² + 6x + 6 = 0, the principles and methods discussed are universally applicable to all quadratic equations. The ability to solve these equations is a cornerstone of mathematical literacy, opening doors to understanding more complex mathematical concepts and their real-world implications.
Frequently Asked Questions (FAQ)
-
Q: Why are there two solutions to a quadratic equation? A: Because a parabola (the graphical representation of a quadratic equation) can intersect the x-axis at two points.
-
Q: What if the discriminant is negative? A: If the discriminant (b² - 4ac) is negative, the quadratic equation has two complex roots involving the imaginary unit i (where i² = -1).
-
Q: Can I use a calculator to solve quadratic equations? A: Yes, many calculators have built-in functions to solve quadratic equations, but understanding the underlying methods is crucial for grasping the mathematical concepts.
-
Q: Are there other methods for solving quadratic equations besides those mentioned? A: Yes, numerical methods like the Newton-Raphson method can also be used, especially for equations that are difficult to solve analytically.
Conclusion: The Enduring Significance of x² + 6x + 6 = 0
The equation x² + 6x + 6 = 0 might seem simple at first glance, but its exploration reveals a wealth of mathematical concepts and their practical applications. Mastering the techniques for solving quadratic equations is essential for anyone pursuing studies or careers in STEM fields and beyond. The ability to not only find the solutions but also understand the underlying principles, the nature of the roots, and the broader context of quadratic equations is a significant step towards a deeper appreciation of mathematics and its role in shaping our world. This seemingly simple equation serves as a gateway to understanding more complex mathematical models and their real-world relevance, making it a crucial concept to grasp firmly.
Latest Posts
Latest Posts
-
Deposition From Gas To Solid
Sep 15, 2025
-
Do Crows Eat Other Birds
Sep 15, 2025
-
150 Degrees F To C
Sep 15, 2025
-
Why Must We Conserve Water
Sep 15, 2025
-
Fruits That Start With Z
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 6x 6 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.