X 2 5x 6 0
candidatos
Sep 22, 2025 · 6 min read
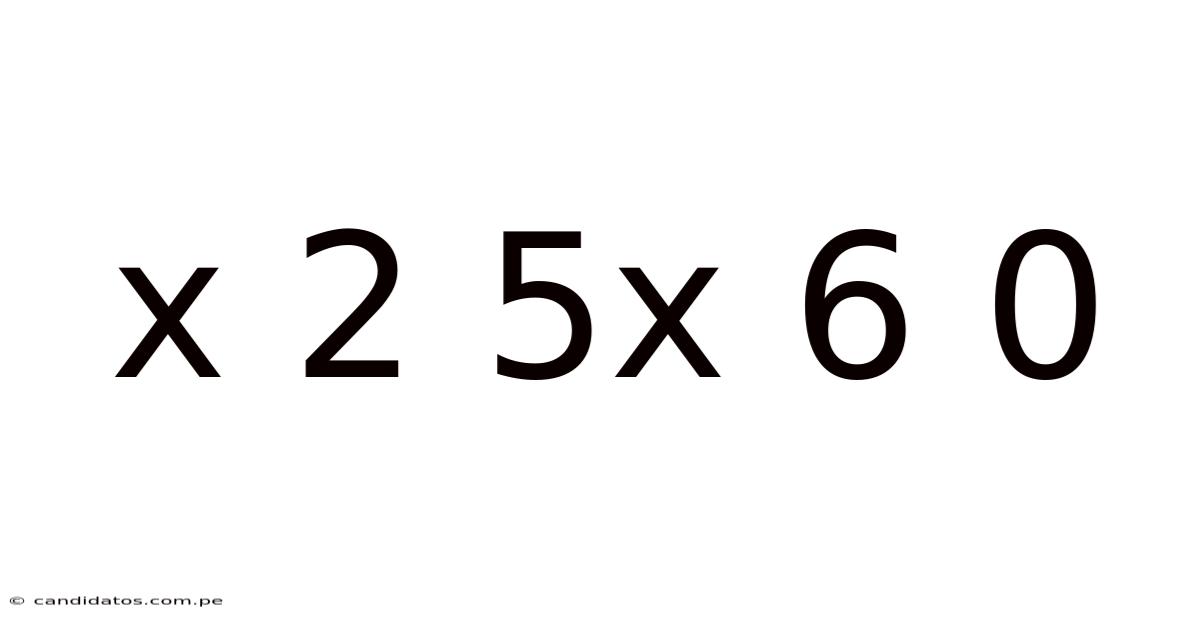
Table of Contents
Decoding the Pattern: Exploring the Mathematical Sequence x 2 5x 6 0
This article delves into the fascinating mathematical puzzle presented by the sequence "x 2 5x 6 0". We'll explore various approaches to understanding this pattern, from simple arithmetic to more advanced algebraic techniques. We aim to not only find a solution but also to illuminate the underlying mathematical principles and problem-solving strategies involved. This exploration will be particularly beneficial for those interested in algebra, pattern recognition, and mathematical problem-solving.
Understanding the Problem: What Does "x 2 5x 6 0" Represent?
At first glance, "x 2 5x 6 0" appears cryptic. However, interpreting it within the context of mathematical sequences, we can assume it represents a series of operations or a function where 'x' is an unknown variable. The sequence suggests a pattern of operations involving multiplication and potentially addition or subtraction. Our goal is to decipher this pattern and determine the value of 'x' or, more broadly, the underlying rule governing this sequence.
Approach 1: Trial and Error – A Practical Starting Point
One straightforward approach is trial and error. We can substitute different values for 'x' and see if they produce a consistent pattern or lead to a meaningful result. Let's try a few values:
- If x = 1: The sequence becomes 1 2 5 6 0. No immediately obvious pattern emerges.
- If x = 2: The sequence becomes 2 4 10 12 0. Still no clear pattern.
- If x = 3: The sequence becomes 3 6 15 18 0. Again, the pattern remains elusive.
While trial and error can be useful for simple problems, it becomes inefficient and unreliable for more complex sequences. It highlights the need for a more systematic and analytical approach.
Approach 2: Algebraic Manipulation – Unveiling the Underlying Function
A more robust method is to approach this problem algebraically. We can assume the sequence represents a function, f(x), where the output depends on the input 'x'. Let's analyze the given numbers (2, 5, 6, 0) as potential results of operations on 'x'.
One possible interpretation is that the sequence represents a series of operations applied to 'x'. Let's consider the possibility of a polynomial function. The simplest polynomial is a linear function: f(x) = ax + b, where 'a' and 'b' are constants. However, a linear function is unlikely to generate the given sequence due to the erratic jumps in values.
Let's explore quadratic functions, of the form f(x) = ax² + bx + c. This allows for more complex patterns. We need at least three data points to solve for the three unknowns (a, b, and c). Let's assume the first three terms in the sequence (2, 5, 6) are the results of the function for x=1, x=2, and x=3 respectively. This gives us the following system of equations:
- a(1)² + b(1) + c = 2
- a(2)² + b(2) + c = 5
- a(3)² + b(3) + c = 6
Solving this system of equations (through methods like substitution or elimination) would potentially give us the values of a, b, and c, thus defining our quadratic function. However, it's important to note that the 0 at the end of the sequence complicates this approach. It might be a separate operation or an indication of a different pattern altogether. This highlights the importance of considering alternative interpretations.
Approach 3: Piecewise Functions – Handling Discontinuities
Given the erratic jump from 6 to 0, we should consider the possibility of a piecewise function. This type of function uses different formulas for different intervals of x. For example, one rule might apply for x ≤ 3 and another for x > 3.
Let's hypothesize a piecewise function with two parts:
- For x ≤ 3: f(x) = ax² + bx + c
- For x > 3: f(x) = g(x) (where g(x) is another function)
We would need to determine the formulas for both f(x) and g(x). The first part could be solved using the same system of equations as before. This would give us an expression for f(x) based on the first three numbers. The function g(x) would need to be determined based on how the sequence continues. If we have further terms, we can extend this approach. Without more data points, however, this remains a hypothesis.
Approach 4: Sequences and Series – Recognizing Recurrence Relations
It's also possible that the sequence doesn't represent a single function but rather a recursive relationship between consecutive terms. This means each term is defined based on the preceding term(s). This is common in many mathematical sequences. For example, we might have a recurrence relation like:
- a<sub>n+1</sub> = f(a<sub>n</sub>)
where a<sub>n</sub> represents the nth term in the sequence. Finding such a recurrence relation requires careful observation of the differences or ratios between consecutive terms. However, with only the limited data provided, identifying a definitive recursive relation is challenging.
Addressing the '0': A Critical Element
The presence of '0' at the end significantly impacts our analysis. It suggests a possible discontinuity or a distinct operation unrelated to the preceding numbers. Possible interpretations include:
- Boundary Condition: The 0 could represent a boundary condition or a limit within a larger mathematical context. Without further information, this remains speculative.
- Separate Operation: The 0 could be the result of a separate operation or function applied after the sequence 2, 5, 6. For instance, it might be the result of a modulus operation or a special condition applied when a certain threshold is reached.
- Error or Incomplete Sequence: It's also possible that the 0 is an error or that the provided sequence is incomplete. More data points would greatly aid in clarifying the pattern.
The Importance of Context: Why More Information is Crucial
The ambiguity in interpreting "x 2 5x 6 0" highlights the importance of context in mathematics. Without additional information, such as:
- The source of the sequence: Where did this sequence come from? A textbook problem? A real-world application?
- Further terms: Are there more numbers in the sequence? This would significantly improve our ability to discern the pattern.
- The intended domain: What are the acceptable values of 'x'? Is it restricted to integers, or are real numbers allowed?
It's impossible to definitively determine the underlying rule governing this sequence. The analysis above showcases various mathematical approaches, highlighting the complexities involved in pattern recognition and problem-solving.
Conclusion: The Art of Mathematical Inquiry
The sequence "x 2 5x 6 0" presents a compelling challenge in mathematical problem-solving. The lack of sufficient data emphasizes the limitations of purely algebraic approaches without adequate context. The process of exploring this puzzle demonstrates the need for flexible thinking, the ability to consider different mathematical models (linear, quadratic, piecewise functions, recursive relations), and the importance of recognizing the limitations of incomplete information. This exercise is a valuable lesson in the art of mathematical inquiry – a process that often involves trial and error, creative hypothesis generation, and careful analysis. Further investigation with more data would be required to fully resolve this puzzle.
Latest Posts
Latest Posts
-
Diff Between Partnership And Company
Sep 22, 2025
-
Meaning Of The Swallow Bird
Sep 22, 2025
-
Unit Of Heat Crossword Clue
Sep 22, 2025
-
A4 Exercise Books 96 Page
Sep 22, 2025
-
What Is An Index Form
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 6 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.