X 2 2x 1 0
candidatos
Sep 15, 2025 · 6 min read
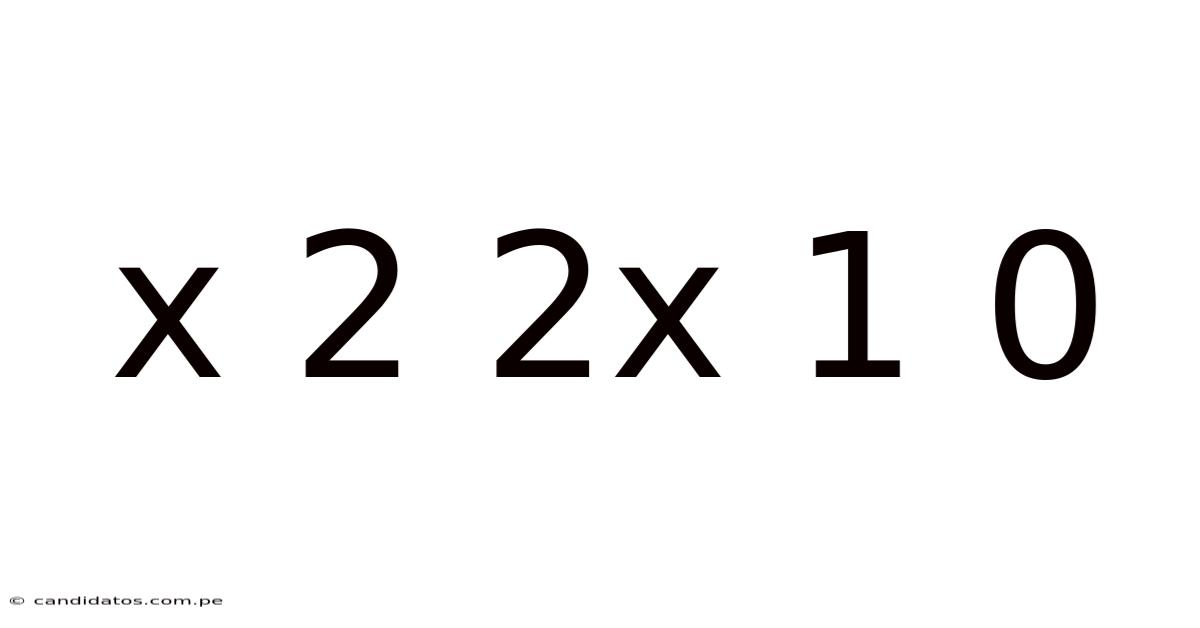
Table of Contents
Deconstructing x² + 2x + 1 = 0: A Deep Dive into Quadratic Equations
This article will explore the quadratic equation x² + 2x + 1 = 0, dissecting its solution methods and broader implications within the field of algebra. We'll move beyond simply finding the solution to understand the underlying principles and connect this seemingly simple equation to more complex mathematical concepts. This comprehensive guide is designed for students of all levels, from those just beginning their algebraic journey to those seeking a deeper understanding of quadratic equations.
Introduction: Understanding Quadratic Equations
A quadratic equation is a second-degree polynomial equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our specific focus, x² + 2x + 1 = 0, falls neatly into this category with a = 1, b = 2, and c = 1. Understanding quadratic equations is crucial in various fields, including physics, engineering, and economics, as they model numerous real-world phenomena involving parabolic curves and rates of change.
Method 1: Factoring the Quadratic Expression
The most straightforward approach to solving x² + 2x + 1 = 0 is through factoring. Notice that the quadratic expression x² + 2x + 1 is a perfect square trinomial. This means it can be factored into the square of a binomial. Recall the formula (a + b)² = a² + 2ab + b². In our case, a = x and b = 1. Therefore:
x² + 2x + 1 = (x + 1)²
Setting this equal to zero gives us:
(x + 1)² = 0
Taking the square root of both sides:
x + 1 = 0
Solving for x:
x = -1
This method reveals that the equation x² + 2x + 1 = 0 has only one real solution, x = -1. This is often referred to as a repeated root or a root of multiplicity two.
Method 2: Using the Quadratic Formula
The quadratic formula provides a general solution for any quadratic equation of the form ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 2, c = 1) into the quadratic formula, we get:
x = [-2 ± √(2² - 4 * 1 * 1)] / (2 * 1) x = [-2 ± √(4 - 4)] / 2 x = [-2 ± √0] / 2 x = -2 / 2 x = -1
Again, we arrive at the solution x = -1. The quadratic formula confirms our previous finding and demonstrates its versatility in solving any quadratic equation, regardless of its factorability.
Method 3: Completing the Square
Completing the square is another powerful technique for solving quadratic equations. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's apply this method to x² + 2x + 1 = 0:
-
Move the constant term to the right side: x² + 2x = -1
-
Take half of the coefficient of the x term (2/2 = 1), square it (1² = 1), and add it to both sides: x² + 2x + 1 = -1 + 1
-
Factor the left side as a perfect square: (x + 1)² = 0
-
Solve for x: x + 1 = 0 x = -1
Completing the square offers a systematic approach, particularly useful when dealing with quadratic equations that are not easily factorable. It also provides insights into the geometric interpretation of quadratic equations.
Graphical Representation and the Discriminant
The equation x² + 2x + 1 = 0 can be represented graphically as a parabola. The parabola intersects the x-axis at the point where y = 0, which represents the solution(s) to the equation. In this case, the parabola only touches the x-axis at x = -1, indicating a single, repeated root.
The discriminant, denoted by Δ (delta), is the expression b² - 4ac within the quadratic formula. The discriminant provides valuable information about the nature of the roots:
- Δ > 0: Two distinct real roots (the parabola intersects the x-axis at two points).
- Δ = 0: One repeated real root (the parabola touches the x-axis at one point).
- Δ < 0: Two complex roots (the parabola does not intersect the x-axis).
For our equation, x² + 2x + 1 = 0, the discriminant is:
Δ = 2² - 4 * 1 * 1 = 0
This confirms that the equation has one repeated real root, which aligns with our previous findings.
Exploring the Significance of Repeated Roots
The fact that x² + 2x + 1 = 0 has a repeated root has important mathematical implications. It signifies that the parabola is tangent to the x-axis at the point (-1, 0). This tangency suggests a point of criticality or a turning point in the function represented by the quadratic. Repeated roots often arise in situations where a system or process reaches an equilibrium or a critical state.
Applications in Calculus and Beyond
Understanding quadratic equations is fundamental in calculus. The derivative of a quadratic function is a linear function, and finding the roots of the derivative helps identify critical points (maxima or minima) of the quadratic function. For instance, the derivative of f(x) = x² + 2x + 1 is f'(x) = 2x + 2. Setting f'(x) = 0 gives x = -1, which corresponds to the minimum point of the parabola.
Furthermore, quadratic equations are used extensively in physics to model projectile motion, the path of a ball or rocket. They are also essential in engineering for designing structures and analyzing stresses. Economic models often utilize quadratic equations to describe cost functions or to optimize resource allocation.
Frequently Asked Questions (FAQ)
-
Q: Can I solve this equation using graphical methods? A: Yes, you can graph the function y = x² + 2x + 1 and find the x-intercept(s), which represent the solution(s) to the equation. In this case, the x-intercept is at x = -1.
-
Q: What if the constant term (c) was different? A: Changing the value of 'c' would alter the parabola's vertical position and potentially change the number and nature of the roots.
-
Q: Are there other methods to solve quadratic equations? A: Yes, numerical methods such as the Newton-Raphson method can be used to approximate the roots of more complex quadratic equations that are difficult to solve analytically.
-
Q: Why is understanding repeated roots important? A: Repeated roots often indicate points of equilibrium, critical points, or turning points in systems modeled by quadratic equations.
Conclusion: A Foundation for Further Exploration
The seemingly simple equation x² + 2x + 1 = 0 serves as a strong foundation for understanding the broader concept of quadratic equations. Through factoring, the quadratic formula, and completing the square, we have explored different approaches to finding its solution. The significance of the repeated root and the discriminant underscores the richness of this equation and its connections to various mathematical fields. This deep dive should equip you with a solid understanding not only of solving this specific equation, but also of tackling more complex quadratic equations and their applications in a range of disciplines. Further exploration into more advanced mathematical concepts will build upon this fundamental knowledge, highlighting the continuous interconnectedness within the world of mathematics.
Latest Posts
Latest Posts
-
Layers Of Retina On Oct
Sep 15, 2025
-
1 Square Foot In Cm
Sep 15, 2025
-
What Acids Are In Batteries
Sep 15, 2025
-
Why Is Polypeptide Synthesis Important
Sep 15, 2025
-
Words That Start With Za
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 1 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.