Whats 5 Percent Of 2000
candidatos
Sep 18, 2025 · 5 min read
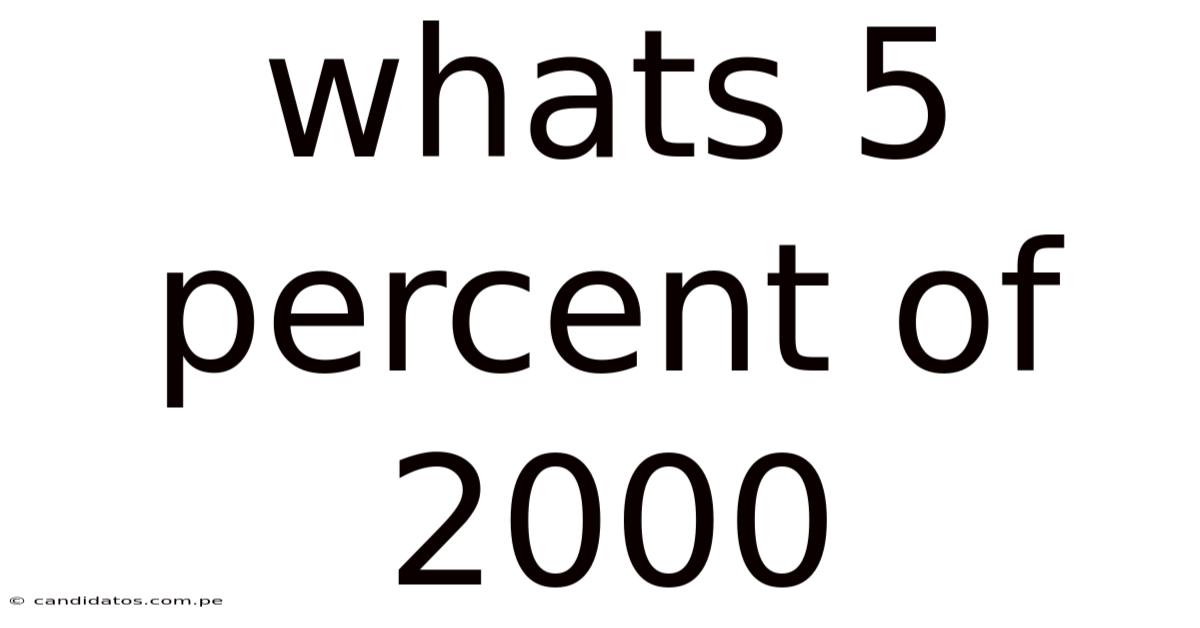
Table of Contents
What's 5 Percent of 2000? A Deep Dive into Percentages and Their Applications
Finding 5 percent of 2000 might seem like a simple calculation, but understanding the underlying principles of percentages unlocks a powerful tool applicable across various fields – from finance and budgeting to sales and statistics. This article will not only answer the question directly but also explore the methods for calculating percentages, their real-world applications, and address common misconceptions. We'll delve into the 'why' behind the calculation, making it more than just a simple arithmetic problem.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent" or "out of one hundred." So, 5% means 5 out of every 100, or 5/100. This can be expressed as a decimal (0.05) or a fraction (1/20). Understanding these equivalent representations is crucial for calculating percentages efficiently.
Methods for Calculating 5% of 2000
There are several ways to calculate 5% of 2000, each offering a different approach and highlighting the flexibility of percentage calculations:
1. The Decimal Method:
This is perhaps the most straightforward method. We convert the percentage to its decimal equivalent and multiply it by the number.
- Step 1: Convert 5% to a decimal: 5% = 5/100 = 0.05
- Step 2: Multiply the decimal by 2000: 0.05 x 2000 = 100
Therefore, 5% of 2000 is 100.
2. The Fraction Method:
This method uses the fractional representation of the percentage.
- Step 1: Convert 5% to a fraction: 5% = 5/100 = 1/20
- Step 2: Multiply the fraction by 2000: (1/20) x 2000 = 2000/20 = 100
Again, 5% of 2000 is 100.
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value.
- Step 1: Set up a proportion: 5/100 = x/2000 (where 'x' represents 5% of 2000)
- Step 2: Cross-multiply: 100x = 5 x 2000 = 10000
- Step 3: Solve for x: x = 10000/100 = 100
Once more, the answer is 100.
4. Using a Calculator:
Most calculators have a percentage function. Simply enter 2000, press the multiplication button, enter 5, and then press the "%" button. The calculator will automatically perform the calculation and display the result: 100.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous real-world scenarios:
-
Finance and Budgeting: Calculating interest on loans, savings account gains, taxes, discounts, and tips all involve percentage calculations. Understanding percentages allows for effective financial planning and management. For example, calculating the VAT (Value Added Tax) on a purchase, determining the discount amount on sale items, or figuring out the interest earned on investments. If you invest $2000 and earn 5% interest, you'll gain $100.
-
Sales and Marketing: Companies use percentages to track sales growth, analyze market share, and determine the effectiveness of marketing campaigns. Understanding percentage changes helps businesses make informed decisions about pricing, promotions, and resource allocation. A 5% increase in sales from one quarter to the next signifies a significant improvement in performance.
-
Statistics and Data Analysis: Percentages are fundamental to representing and interpreting data. They help to visualize proportions, trends, and comparisons within datasets. For example, presenting survey results where 5% of respondents chose a particular option.
-
Science and Engineering: Percentage calculations are used in various scientific and engineering applications, such as calculating error margins, determining concentrations of solutions, and expressing experimental results.
-
Everyday Life: Calculating discounts at stores, determining the tip amount in restaurants, or understanding nutritional information on food labels all involve the application of percentages.
Common Misconceptions about Percentages
Several common misconceptions surround percentage calculations:
-
Adding Percentages: It's incorrect to simply add percentages directly when dealing with different base amounts. For instance, a 5% increase followed by a 5% decrease does not result in the original amount. The percentage change is calculated on the new base amount each time.
-
Percentage Points vs. Percentages: It's crucial to distinguish between percentage points and percentages. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase (5/10 = 0.5 or 50%). This distinction is particularly important when analyzing economic or social data.
-
Percentage of a Percentage: Calculating a percentage of a percentage requires multiplying the percentages in their decimal form. For instance, 5% of 10% is calculated as 0.05 x 0.10 = 0.005 or 0.5%.
Frequently Asked Questions (FAQs)
-
Q: How do I calculate x% of y? A: Convert x% to a decimal (x/100) and multiply it by y.
-
Q: What is the formula for percentage change? A: [(New Value - Old Value) / Old Value] x 100
-
Q: How do I calculate the percentage increase or decrease? A: Calculate the difference between the new and old values, divide by the old value, and multiply by 100. A positive result indicates an increase, while a negative result indicates a decrease.
-
Q: Can I use percentages to compare different sized quantities? A: Yes, percentages allow for meaningful comparisons between quantities of different sizes, providing a standardized measure of proportion.
Conclusion: Mastering Percentages – A Valuable Skill
Calculating 5% of 2000, as we've seen, yields the answer 100. However, the true value lies in understanding the underlying concepts and the wide-ranging applications of percentage calculations. From managing personal finances to analyzing complex data, the ability to work confidently with percentages is a valuable skill that enhances problem-solving abilities across various fields. This understanding isn't limited to simple arithmetic; it unlocks a pathway to more effective decision-making and a deeper understanding of the numerical world around us. Therefore, mastering percentages is an investment in your intellectual growth and practical capabilities. By grasping the different methods and avoiding common pitfalls, you equip yourself with a tool that will serve you well throughout life.
Latest Posts
Latest Posts
-
5 Letter Words Starting Ma
Sep 18, 2025
-
What Percent Is 1 15
Sep 18, 2025
-
Reaction Of Nh3 With Water
Sep 18, 2025
-
Convert 130 Lbs To Kg
Sep 18, 2025
-
Words Starting With A I
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Whats 5 Percent Of 2000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.