What Percent Is 19 25
candidatos
Sep 20, 2025 · 5 min read
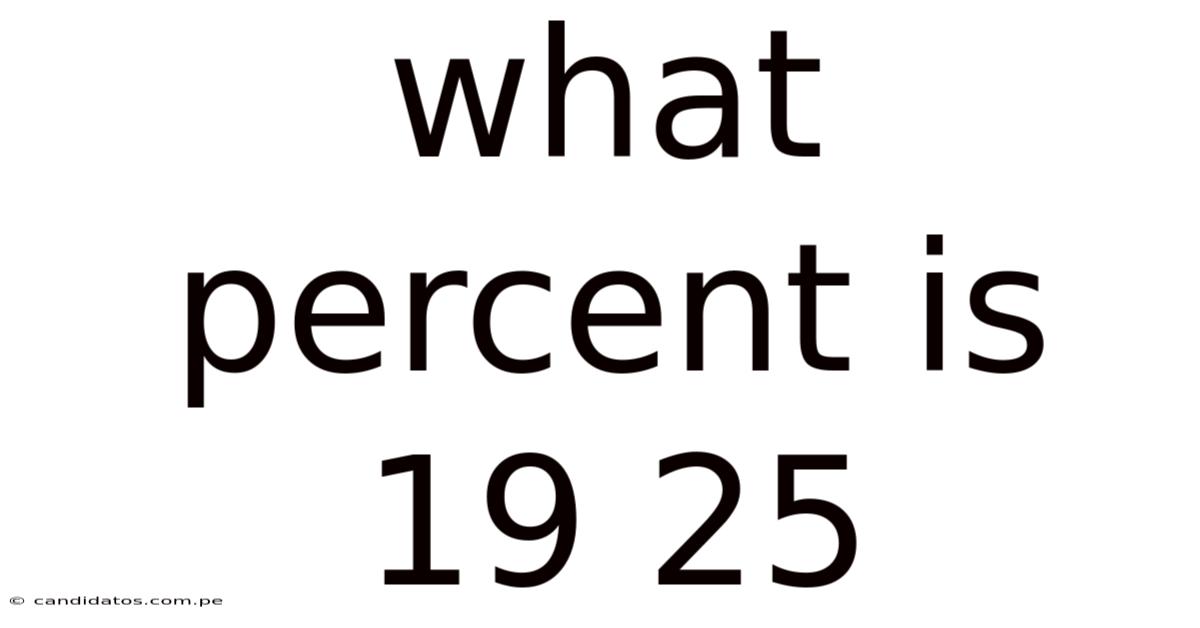
Table of Contents
What Percent is 19 of 25? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will thoroughly explore how to determine what percent 19 is of 25, providing not only the answer but also a comprehensive explanation of the underlying concepts and various methods for solving similar problems. We'll cover the basic principles, delve into different calculation approaches, and explore real-world examples to solidify your understanding.
Introduction: Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are a useful way to represent proportions and comparisons, making them easier to understand and interpret than fractions or decimals alone.
Method 1: Using the Formula
The most straightforward method to calculate what percent 19 is of 25 involves using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 19 (the number we want to express as a percentage of the whole)
- Whole: 25 (the total amount)
Substituting these values into the formula:
(19 / 25) x 100% = 0.76 x 100% = 76%
Therefore, 19 is 76% of 25.
Method 2: Converting to a Decimal and then to a Percentage
This method involves two steps:
-
Convert the fraction to a decimal: Divide the part (19) by the whole (25): 19 ÷ 25 = 0.76
-
Convert the decimal to a percentage: Multiply the decimal by 100%: 0.76 x 100% = 76%
This method is particularly useful when working with calculators, as it simplifies the calculation process.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We can set up a proportion:
19/25 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we can cross-multiply:
19 * 100 = 25 * x
1900 = 25x
x = 1900 / 25
x = 76
Therefore, x = 76%, confirming our previous results. This method demonstrates the relationship between fractions, decimals, and percentages in a clear and concise manner.
Understanding the Concept: Part, Whole, and Percentage
It's crucial to clearly identify the "part" and the "whole" in any percentage problem. The part is the smaller quantity that you're comparing to the whole, which is the larger, total quantity. The percentage then represents the proportion of the part relative to the whole. Misidentifying the part and whole will lead to incorrect results.
In our example, 19 is the part, and 25 is the whole. Understanding this distinction is crucial for solving a wide range of percentage problems, not just this specific one. Consider a scenario where you're calculating the percentage of students who passed an exam. The number of students who passed is the part, and the total number of students is the whole.
Real-World Applications: Where Percentages Matter
Percentages are ubiquitous in our daily lives. Understanding them is essential for navigating various situations effectively. Here are a few examples:
-
Retail Discounts: Stores frequently offer discounts as percentages. If a $50 item is discounted by 20%, you'll need to calculate the discount amount (20% of $50) and subtract it from the original price.
-
Taxes: Sales taxes are usually expressed as a percentage of the purchase price. Calculating the final price requires adding the tax percentage to the original price.
-
Financial Reports: Companies use percentages extensively in their financial reports to represent growth, profit margins, and other key metrics. Understanding these percentages is vital for interpreting financial performance.
-
Statistics and Data Analysis: Percentages are fundamental in statistics. They're used to present data in a clear, concise, and easily comparable manner. Opinion polls, election results, and scientific studies frequently use percentages to summarize findings.
-
Grade Calculations: In many educational systems, grades are expressed as percentages. Understanding your percentage grade helps you track your academic progress and identify areas for improvement.
Beyond the Basics: More Complex Percentage Problems
While the problem of determining what percent 19 is of 25 is relatively straightforward, the underlying principles can be applied to more complex percentage problems. These often involve finding the part, the whole, or the percentage itself, given the other two values. For instance:
-
Finding the Part: If 30% of a number is 15, what is the number? (This involves working backward from the percentage and part to find the whole).
-
Finding the Whole: If 12 is 25% of a number, what is that number? (Similar to the previous example, but with a different unknown).
-
Finding the Percentage Increase or Decrease: If a value increases from 50 to 60, what is the percentage increase? This involves calculating the difference, then expressing it as a percentage of the original value.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve percentage problems?
A: Absolutely! Calculators simplify the process, especially for more complex problems. Most calculators have a percentage function (%) that can be used directly in the calculation.
Q: Why is understanding percentages important?
A: Percentages are a fundamental tool for understanding proportions and comparisons, making them essential for interpreting data, making financial decisions, and solving numerous everyday problems.
Q: What if the numbers aren't whole numbers?
A: The same principles apply even if the numbers have decimal places. Use the same formulas, but be careful with your calculations to ensure accuracy.
Q: Are there other methods for calculating percentages?
A: Yes, various other methods exist, including using ratios, proportions, and visual aids such as pie charts or bar graphs. The most efficient method often depends on the specific problem and your comfort level with different mathematical approaches.
Conclusion: Mastering Percentages for Everyday Life
Calculating what percent 19 is of 25 – which we've established is 76% – is a simple yet illustrative example of the broader concept of percentages. Mastering percentage calculations is not just about solving math problems; it's about gaining a powerful tool for understanding and navigating the quantitative aspects of our daily lives. By understanding the underlying principles, different calculation methods, and diverse applications, you can confidently tackle percentage problems and use this knowledge to make informed decisions in various contexts. From financial planning to data analysis, the ability to work with percentages effectively empowers you to make sense of the world around you and confidently tackle numerical challenges.
Latest Posts
Latest Posts
-
Bhutan Currency To Australian Dollar
Sep 21, 2025
-
Cubic Metre To Cubic Centimetre
Sep 21, 2025
-
9 11 As A Percent
Sep 21, 2025
-
Reverse Osmosis Water Filtration Diagram
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 19 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.