What Is Half Of 90
candidatos
Sep 18, 2025 · 6 min read
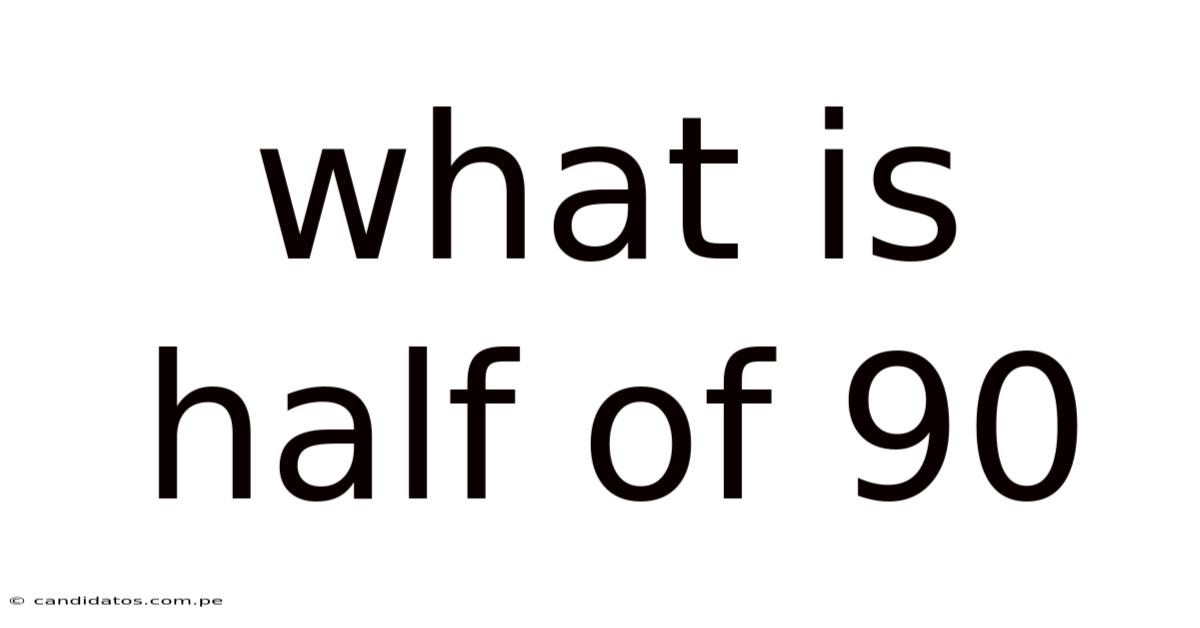
Table of Contents
What is Half of 90? A Deep Dive into Division and its Applications
What is half of 90? The seemingly simple answer, 45, opens a door to a fascinating world of mathematics, encompassing basic arithmetic, fractional understanding, and even real-world applications. This article will explore this seemingly simple question in depth, going beyond the immediate answer to unpack the underlying concepts and demonstrate its relevance in various contexts.
Understanding Division: The Foundation of Finding Half
Before we delve into finding half of 90, let's solidify our understanding of division. Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts. When we ask "what is half of 90?", we are essentially asking to divide 90 into two equal parts.
This can be represented mathematically in several ways:
- 90 ÷ 2 = ? This is the standard division notation, using the division symbol (÷).
- 90 / 2 = ? This uses the forward slash (/) as a division symbol, common in calculators and computer programming.
- ½ × 90 = ? This approach uses a fraction (½, representing one-half) to express the division. Multiplying by a fraction is equivalent to division.
All three representations will yield the same answer: 45.
The Calculation: Finding Half of 90
Finding half of 90 is a straightforward calculation:
90 ÷ 2 = 45
This means that if you divide 90 into two equal groups, each group will contain 45. This is the core of understanding "half." It represents one out of two equal parts of a whole.
Expanding the Concept: Fractions and Percentages
The concept of "half" extends beyond simple division. It's deeply connected to fractions and percentages. "Half" is equivalent to:
- The fraction ½: This represents one part out of two equal parts.
- 50%: This is the percentage representation of one-half, meaning 50 out of 100.
Understanding these interconnections allows us to solve related problems. For instance, if a question asks for 50% of 90, the solution remains the same: 45.
Real-World Applications: Where Half of 90 Matters
The seemingly trivial calculation of "half of 90" has numerous practical applications in daily life:
- Sharing: Imagine sharing 90 cookies equally between two friends. Each friend receives 45 cookies.
- Measurement: If you need to cut a 90-centimeter piece of wood in half, each piece will be 45 centimeters long.
- Cooking: A recipe calling for 90 grams of flour might require you to use 45 grams for half the recipe.
- Finance: If you have $90 and want to save half, you will save $45.
- Data Analysis: In statistics, finding the midpoint of a dataset often involves dividing the total by two. If a dataset sums to 90, the midpoint is 45.
These examples showcase how fundamental the concept of "half" is in practical scenarios. It's a building block for more complex calculations and problem-solving.
Beyond the Basics: Exploring Related Concepts
Understanding "half of 90" lays the groundwork for understanding more complex fractional and proportional relationships:
- Thirds, Fourths, and Other Fractions: Once you grasp the concept of halving, extending it to other fractions becomes easier. Finding one-third of 90 (90 ÷ 3 = 30) or one-fourth of 90 (90 ÷ 4 = 22.5) follows the same logic.
- Proportions: Proportional reasoning builds upon the ability to find fractions of a whole. For instance, if you know that half of a quantity is 45, you can easily determine the whole quantity (45 x 2 = 90) or other fractions of the whole.
- Ratios: Ratios express the relationship between two or more quantities. Understanding fractions is crucial for working with ratios. For example, a ratio of 1:2 represents one part to two parts, similar to the concept of a half.
Mathematical Properties: Exploring the Nature of Division
Let's examine the mathematical properties relevant to finding half of 90:
- Commutative Property (Does Not Apply): Unlike addition and multiplication, division is not commutative. This means that 90 ÷ 2 is not the same as 2 ÷ 90.
- Associative Property (Does Not Apply): Similarly, division is not associative. This means that (90 ÷ 2) ÷ 1 is not the same as 90 ÷ (2 ÷ 1).
- Distributive Property (Applies with Caution): The distributive property applies when dividing a sum by a number, but not when dividing a number by a sum. For instance, (60 + 30) ÷ 2 is the same as (60 ÷ 2) + (30 ÷ 2) = 45. However, 90 ÷ (2 + 1) is not the same as (90 ÷ 2) + (90 ÷ 1).
Expanding the Scope: Working with Larger Numbers and Decimals
The principle of finding half applies equally well to larger numbers and decimals:
- Finding half of larger numbers: To find half of 180, simply divide 180 by 2 (180 ÷ 2 = 90). The process remains consistent.
- Finding half of decimals: Finding half of 90.5 would involve dividing 90.5 by 2 (90.5 ÷ 2 = 45.25). The same principle applies, even with decimal numbers.
The ability to find half of various numbers is essential for many areas of mathematics and everyday problem-solving.
Frequently Asked Questions (FAQ)
-
Q: What if I want to find more than half of 90?
- A: To find a specific fraction or percentage of 90, multiply 90 by that fraction or percentage. For example, to find three-quarters (¾) of 90, calculate (¾) x 90 = 67.5.
-
Q: How can I calculate half of a number quickly in my head?
- A: For even numbers, simply divide the number by 2. For odd numbers, you can divide the number one less than the number by 2 and then add 0.5. For example, half of 91 is (90/2) + 0.5 = 45.5. Alternatively, many people find it helpful to divide the number by 10 and then double the result (90/10 = 9; 9 x 5 = 45).
-
Q: Is there a way to find half of a number without using division?
- A: Yes. You can use repeated subtraction. Subtract 2 repeatedly from the number until you reach 0. The number of times you subtracted 2 will be half the original number. This method is less efficient for larger numbers, but it illustrates the underlying concept of division.
-
Q: Are there different ways to represent “half”?
- A: Yes, besides ½ and 50%, “half” can also be represented as 0.5 (decimal), 1/2 (fraction), or even as a ratio (1:1). The representation may vary depending on the context.
Conclusion: The Significance of a Simple Calculation
While the question "What is half of 90?" seems deceptively simple, it serves as a gateway to a rich understanding of fundamental mathematical concepts. From basic arithmetic and fractional understanding to real-world applications and the exploration of mathematical properties, the answer – 45 – unveils a deeper mathematical landscape. Mastering this seemingly simple calculation is a crucial step in developing stronger mathematical skills and applying them effectively in various situations. The ability to quickly and accurately calculate halves, and other fractions, is a valuable tool for navigating the world around us.
Latest Posts
Latest Posts
-
Example Of Liquid Gas Solution
Sep 18, 2025
-
Parametric And Non Parametric Testing
Sep 18, 2025
-
Number Line With Minus Numbers
Sep 18, 2025
-
Words That Describe A Forest
Sep 18, 2025
-
First Order Linear Recurrence Relation
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.