Two Thirds As A Percentage
candidatos
Sep 17, 2025 · 5 min read
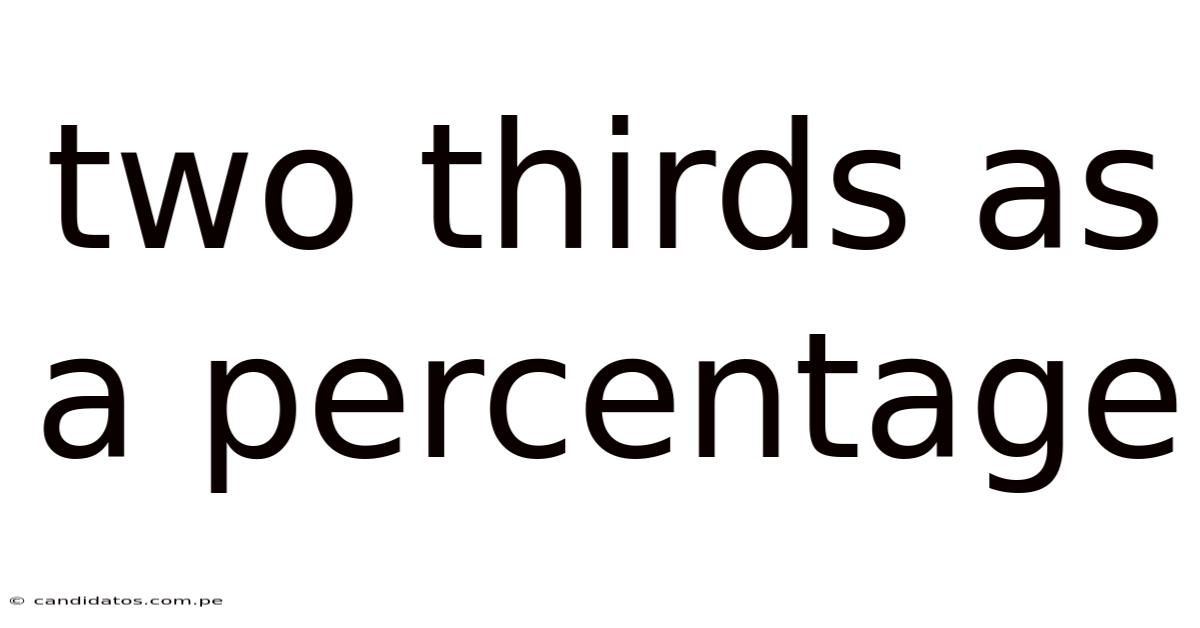
Table of Contents
Two-Thirds as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications across various fields, from everyday budgeting to complex scientific calculations. This article delves into the conversion of two-thirds to a percentage, explaining the process in detail and exploring its practical applications. We'll cover the method, provide examples, and address common questions surrounding this seemingly simple yet important concept.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction ⅔, 2 is the numerator and 3 is the denominator, indicating two parts out of a total of three parts.
A percentage, on the other hand, expresses a fraction as a portion of 100. The symbol % denotes "per cent" or "out of 100". Therefore, 50% means 50 out of 100, which is equivalent to the fraction ½.
Converting Two-Thirds to a Percentage
Converting two-thirds (⅔) to a percentage involves two main steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator by the denominator:
2 ÷ 3 = 0.666666...
Notice that the decimal representation of ⅔ is a repeating decimal. This means the digit 6 repeats infinitely. For practical purposes, we often round this to a certain number of decimal places.
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.666666... × 100 ≈ 66.67%
Therefore, two-thirds is approximately equal to 66.67%. The use of "approximately" is crucial here because we've rounded the repeating decimal. The exact percentage representation of ⅔ is 66.666...%, with the 6 repeating infinitely.
Different Methods for Conversion
While the above method is the most straightforward, let's explore alternative approaches:
Method 1: Using Proportions
We can set up a proportion to find the equivalent percentage:
⅔ = x/100
Cross-multiplying, we get:
3x = 200
x = 200/3 ≈ 66.67
Therefore, x ≈ 66.67%, confirming our previous result.
Method 2: Direct Conversion Using a Calculator
Most calculators have a fraction-to-decimal conversion function. Inputting ⅔ and pressing the equals button will directly give you the decimal value (0.666666...). Multiplying this by 100 gives the percentage.
Practical Applications of Two-Thirds as a Percentage
The concept of two-thirds as a percentage finds its use in various scenarios:
- Sales and Discounts: A store might offer a discount of two-thirds on selected items, meaning a 66.67% reduction in price.
- Surveys and Statistics: If two-thirds of respondents in a survey agree with a particular statement, it represents 66.67% agreement.
- Data Analysis: In data analysis, two-thirds might represent a significant portion of a dataset, requiring closer examination.
- Recipe Adjustments: When adjusting recipes, scaling ingredients up or down by two-thirds (66.67%) is a common practice.
- Finance: Calculating interest or returns based on fractional proportions often involves converting fractions to percentages for easier understanding and comparison.
Understanding the Repeating Decimal
The repeating decimal 0.666... is a fascinating aspect of this conversion. This is because ⅔ represents a rational number – a number that can be expressed as a fraction of two integers. However, its decimal representation is non-terminating (it goes on forever) and repeating. This highlights the relationship between fractions and decimals, and the limitations of representing some rational numbers precisely in decimal form.
Rounding and Precision
When working with percentages, it's important to consider the level of precision required. For many practical purposes, rounding 66.666...% to 66.67% is sufficient. However, in situations demanding higher accuracy (e.g., financial calculations), using more decimal places or expressing the answer as a fraction (⅔) might be necessary to avoid rounding errors accumulating over multiple calculations.
Frequently Asked Questions (FAQ)
Q: Is 66.67% the exact equivalent of two-thirds?
A: No, 66.67% is an approximation of two-thirds. The exact value is 66.666...%, with the 6 repeating infinitely.
Q: How do I calculate two-thirds of a number?
A: To calculate two-thirds of a number, multiply the number by ⅔ or its decimal equivalent (approximately 0.6667).
Q: Can I use 67% instead of 66.67% for simplicity?
A: While 67% is a close approximation, using 66.67% provides greater accuracy. The choice depends on the context and the acceptable level of error. For most everyday situations, 67% might suffice, but in more precise contexts, using 66.67% is preferable.
Q: What are some other common fractions and their percentage equivalents?
A: Some other common fraction-percentage equivalents include: ½ = 50%, ¼ = 25%, ¾ = 75%, ⅛ = 12.5%, ⅜ = 37.5%, ⅝ = 62.5%, ⅞ = 87.5%.
Conclusion
Converting two-thirds to a percentage is a straightforward process involving dividing the numerator by the denominator to obtain a decimal, then multiplying by 100 to get the percentage. Understanding this conversion is essential for various applications in everyday life and more complex mathematical and scientific contexts. While 66.67% is a commonly used approximation, remembering the repeating nature of the decimal representation emphasizes the nuances of mathematical conversions and the importance of choosing an appropriate level of precision based on the situation. Mastering this seemingly simple conversion lays a strong foundation for tackling more advanced mathematical concepts and problem-solving in diverse fields.
Latest Posts
Latest Posts
-
G Ml To Kg M3
Sep 17, 2025
-
21 Out Of 30 Percentage
Sep 17, 2025
-
Different Shapes And Their Names
Sep 17, 2025
-
What Is The Promissory Note
Sep 17, 2025
-
How To Draw A Candle
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Two Thirds As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.