Square Root Of 1 Half
candidatos
Sep 24, 2025 · 5 min read
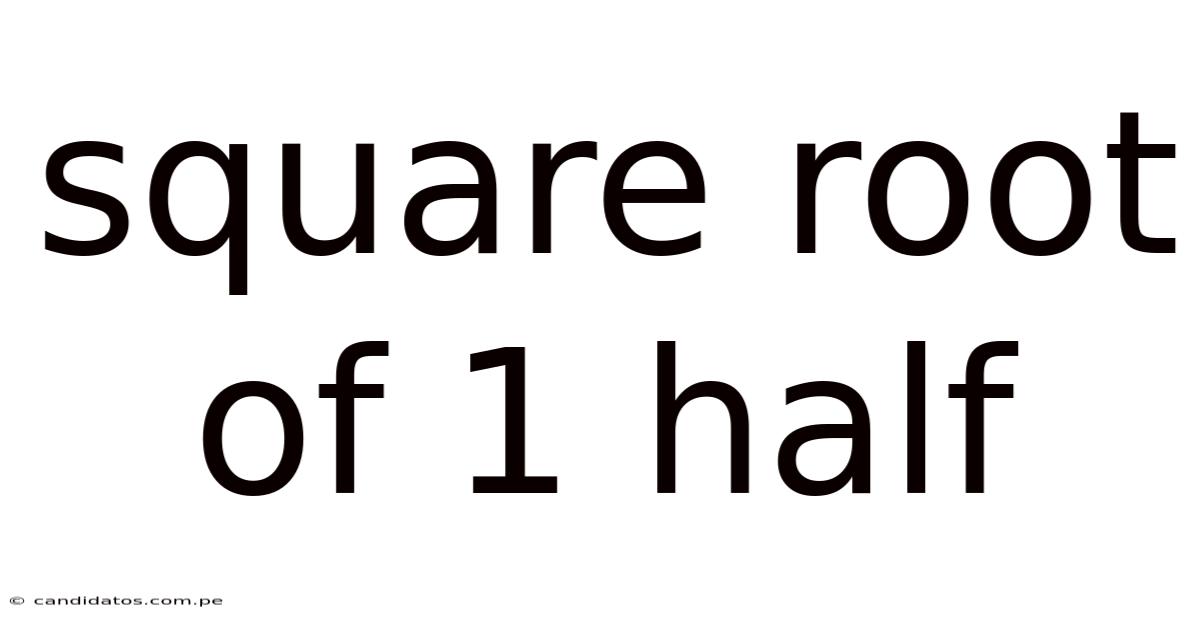
Table of Contents
Decoding the Mystery: Understanding the Square Root of One Half
Finding the square root of one half (√½) might seem like a simple mathematical problem, but it opens a door to a deeper understanding of fundamental mathematical concepts. This seemingly straightforward calculation delves into the realms of fractions, decimals, radicals, and even the Pythagorean theorem. This comprehensive guide will explore the square root of one half, providing a detailed explanation suitable for various levels of mathematical understanding, from beginners to those seeking a more in-depth analysis. We'll unravel the process step-by-step, explaining the underlying principles and offering various approaches to solving this problem.
Understanding Square Roots
Before we delve into the specifics of √½, let's refresh our understanding of square roots. The square root of a number is a value that, when multiplied by itself (squared), equals the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. Square roots are the inverse operation of squaring a number. This fundamental concept forms the basis of our exploration.
Calculating the Square Root of One Half: The Step-by-Step Approach
There are several ways to calculate the square root of one half. Let's explore the most common and intuitive methods:
Method 1: Simplifying the Fraction
The simplest approach involves simplifying the fraction before calculating the square root. Remember that √½ is the same as √(1/2). We can rewrite this as:
√(1/2) = √1 / √2
The square root of 1 is simply 1. Therefore, we have:
1 / √2
This is a perfectly valid answer, but it’s often preferred to rationalize the denominator (remove the square root from the bottom of the fraction).
Method 2: Rationalizing the Denominator
To rationalize the denominator, we multiply both the numerator and the denominator by √2:
(1 / √2) * (√2 / √2) = √2 / 2
This gives us our final, rationalized answer: √2 / 2. This form is generally preferred because it's cleaner and easier to work with in further calculations.
Method 3: Using Decimal Approximation
We can also approximate the square root of one half using decimal values. Since ½ is equal to 0.5, we can find the square root of 0.5:
√0.5 ≈ 0.7071
This is an approximate value, as the square root of 0.5 is an irrational number (a number that cannot be expressed as a simple fraction). The decimal approximation is useful for practical applications where a precise value isn't strictly necessary. However, remember this is an approximation and not the exact value.
Understanding the Irrational Nature of √½
The square root of one half, whether expressed as √2/2 or approximately 0.7071, is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Irrational numbers have decimal representations that continue infinitely without repeating. Understanding this property is crucial for comprehending the nature of the result.
Connecting to the Pythagorean Theorem
The square root of one half appears frequently in geometry, particularly when dealing with isosceles right-angled triangles. Consider a right-angled triangle with two legs of equal length (let's say, length 'a'). According to the Pythagorean theorem (a² + b² = c²), the hypotenuse (c) can be calculated as:
c² = a² + a² = 2a²
Therefore, c = √(2a²) = a√2
If we consider a right-angled isosceles triangle with legs of length 1, the hypotenuse would be √2. The ratio of one leg to the hypotenuse would be 1/√2, which simplifies to √2/2. This connection highlights the geometric significance of √½.
Practical Applications of √½
The square root of one half has various applications across different fields:
- Trigonometry: It appears frequently in trigonometric calculations, particularly involving angles of 45 degrees.
- Physics and Engineering: It's used in vector calculations, especially those involving forces or velocities at right angles.
- Computer Graphics: It plays a role in transformations and rotations in 2D and 3D graphics.
- Probability and Statistics: It may appear in calculations related to normal distributions and standard deviations.
Advanced Mathematical Considerations
For those interested in a deeper dive, here are some advanced considerations:
- Continued Fractions: √½ can be expressed as a continued fraction, offering another way to approximate its value.
- Taylor Series Expansion: The square root function can be represented using a Taylor series expansion, allowing for a calculation using an infinite series.
- Complex Numbers: While we’ve focused on real numbers, the concept of square roots extends to complex numbers, adding another layer of complexity.
Frequently Asked Questions (FAQ)
Q: Is √½ the same as ½?
A: No, they are different. √½ is the number that, when multiplied by itself, equals ½. ½ is simply one-half.
Q: Can I use a calculator to find the square root of one half?
A: Yes, most scientific calculators have a square root function (√). You can directly input 0.5 or ½ and find the approximate decimal value.
Q: Why is it important to rationalize the denominator?
A: Rationalizing the denominator simplifies the expression, making it easier to work with in subsequent calculations and avoids potential complications when working with irrational numbers.
Q: What is the exact value of √½?
A: The exact value is √2/2. It's an irrational number, meaning its decimal representation goes on infinitely without repeating.
Conclusion
The square root of one half, seemingly a simple problem, offers a rich tapestry of mathematical concepts. From the fundamental understanding of square roots and fractions to the rationalization of denominators and its connection to the Pythagorean theorem, this exploration has illuminated various facets of mathematics. Whether you’re a beginner or an experienced mathematician, grasping the concepts surrounding √½ strengthens your overall mathematical foundation and unveils the beauty and elegance hidden within seemingly simple calculations. The journey to understanding this seemingly simple calculation opens up a world of opportunities to explore more complex mathematical concepts and their practical applications. Remember, mathematics is not just about finding answers; it's about understanding the journey and appreciating the intricacies of the process.
Latest Posts
Latest Posts
-
Rates And Ratios Year 8
Sep 24, 2025
-
M B B S Full Form In Medical
Sep 24, 2025
-
1
Sep 24, 2025
-
Routing Protocols And Routed Protocols
Sep 24, 2025
-
Exciting Crossword Clue 9 Letters
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 1 Half . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.