Lcm Of 9 And 15
candidatos
Sep 20, 2025 · 6 min read
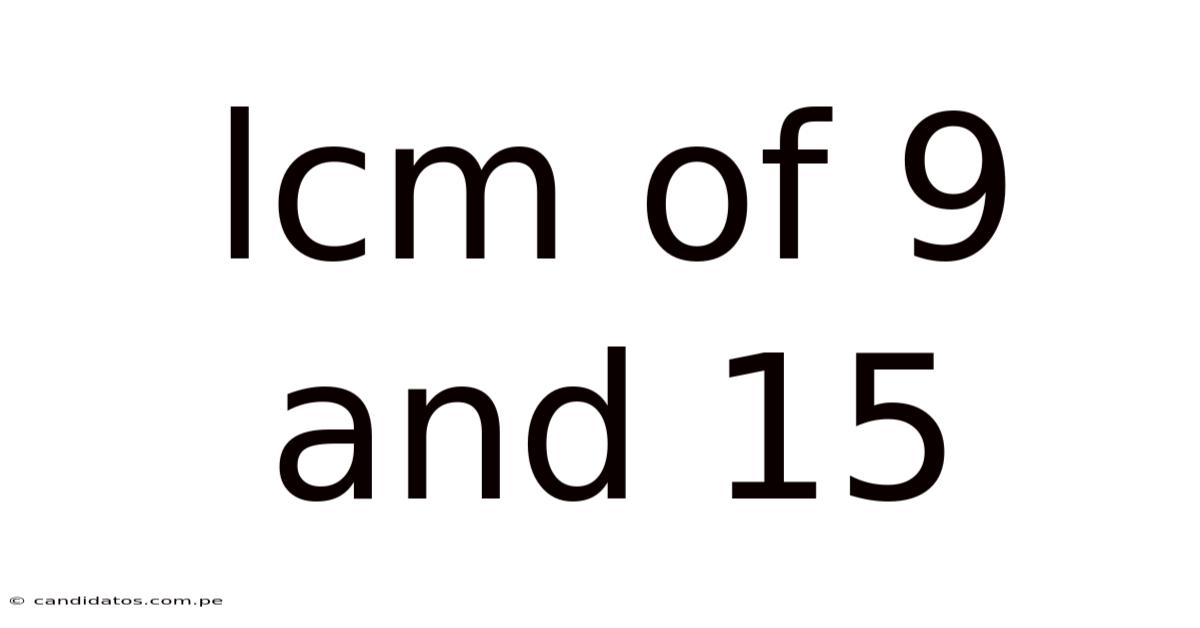
Table of Contents
Finding the Least Common Multiple (LCM) of 9 and 15: A Comprehensive Guide
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it is crucial for building a strong foundation in mathematics. This comprehensive guide will explore the LCM of 9 and 15, delving into different approaches, explaining the underlying principles, and providing you with the tools to tackle similar problems with confidence. We'll cover everything from the basic definition of LCM to advanced techniques, ensuring you have a complete grasp of the topic.
Introduction: What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers in the set as factors. For example, finding the LCM of 9 and 15 means finding the smallest positive number that is divisible by both 9 and 15 without leaving a remainder. This concept is fundamental in various mathematical applications, including fractions, algebra, and even more advanced areas like number theory.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. Let's start by listing the multiples of 9 and 15:
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, ...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, ...
By comparing the two lists, we can identify the common multiples. The smallest common multiple is 45. Therefore, the LCM of 9 and 15 is 45.
This method is easy to understand but becomes less efficient when dealing with larger numbers. Imagine trying to list the multiples of 127 and 255 – it would be quite tedious! That’s where other methods come in handy.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM, especially for larger numbers. It involves breaking down each number into its prime factors – the prime numbers that multiply together to give the original number.
Let's factorize 9 and 15:
- 9 = 3 x 3 = 3²
- 15 = 3 x 5
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
Multiply these highest powers together: 9 x 5 = 45. Therefore, the LCM of 9 and 15 is 45.
This method is significantly more efficient than listing multiples, especially for larger numbers. It provides a systematic approach that is less prone to errors.
Method 3: Using the Greatest Common Divisor (GCD)
The Greatest Common Divisor (GCD) is the largest positive integer that divides both numbers without leaving a remainder. There's a useful relationship between the LCM and GCD of two numbers:
LCM(a, b) x GCD(a, b) = a x b
This formula provides an alternative way to calculate the LCM. First, let's find the GCD of 9 and 15. We can use the Euclidean algorithm for this:
- Divide the larger number (15) by the smaller number (9): 15 ÷ 9 = 1 with a remainder of 6.
- Replace the larger number with the remainder (6) and repeat: 9 ÷ 6 = 1 with a remainder of 3.
- Repeat: 6 ÷ 3 = 2 with a remainder of 0.
The last non-zero remainder is the GCD, which is 3. Therefore, GCD(9, 15) = 3.
Now, we can use the formula:
LCM(9, 15) = (9 x 15) / GCD(9, 15) = (135) / 3 = 45
This method also provides an efficient way to calculate the LCM, particularly when dealing with larger numbers. The Euclidean algorithm is a very efficient method for finding the GCD.
Method 4: Venn Diagram Approach (Visual Representation)
While not a direct calculation method, a Venn diagram can help visualize the prime factorization and understand the concept of LCM. Let’s represent the prime factorization of 9 and 15 in a Venn diagram:
- 9 (3 x 3): Two '3's go in the section representing only factors of 9.
- 15 (3 x 5): One '3' goes in the overlapping section (common factor), and one '5' goes in the section representing only factors of 15.
To find the LCM, multiply all the numbers in the diagram: 3 x 3 x 5 = 45.
This method is primarily useful for visual learners and helps reinforce the understanding of prime factorization and common factors.
Explanation of the Methods: A Deeper Dive
The methods outlined above all rely on the fundamental principles of prime factorization and divisibility. Understanding these principles is essential to truly grasp the concept of LCM.
-
Prime Factorization: Every integer greater than 1 can be expressed as a unique product of prime numbers. This unique factorization is fundamental to finding the LCM because it allows us to identify the common and uncommon prime factors. The LCM incorporates all prime factors, using the highest power of each factor present in any of the numbers.
-
GCD and the Relationship to LCM: The GCD and LCM are inversely related. A high GCD implies a low LCM and vice versa. The formula LCM(a, b) x GCD(a, b) = a x b stems from the fact that both the GCD and LCM represent the common and uncommon prime factors in a structured way. The GCD accounts for only the shared factors, while the LCM encompasses all factors, ensuring divisibility by both numbers.
Frequently Asked Questions (FAQs)
-
Q: What is the difference between LCM and GCD?
- A: The LCM (Least Common Multiple) is the smallest number divisible by both numbers, while the GCD (Greatest Common Divisor) is the largest number that divides both numbers without a remainder. They are related but represent different aspects of the relationship between two integers.
-
Q: Can the LCM of two numbers be one of the numbers?
- A: Yes. If one number is a multiple of the other, the LCM will be the larger number. For example, the LCM of 6 and 12 is 12.
-
Q: How do I find the LCM of more than two numbers?
- A: You can extend the prime factorization method. Find the prime factorization of each number, then take the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to get the LCM.
-
Q: Why is finding the LCM important?
- A: The LCM is crucial for solving problems involving fractions, particularly when adding or subtracting fractions with different denominators. Finding the LCM of the denominators allows you to find a common denominator, simplifying the calculation. It also has applications in various fields like scheduling and modular arithmetic.
Conclusion: Mastering the LCM
Finding the LCM, whether for 9 and 15 or for larger numbers, is a fundamental mathematical skill. This guide has explored multiple methods – listing multiples, prime factorization, using the GCD, and the visual Venn diagram approach – providing you with a robust understanding of the underlying principles and diverse approaches for solving such problems. By mastering these techniques, you'll not only be able to efficiently calculate the LCM but also develop a deeper appreciation for the interconnectedness of mathematical concepts. Remember to choose the method that works best for you and the context of the problem. With practice, finding the LCM will become second nature, enhancing your mathematical proficiency and problem-solving capabilities.
Latest Posts
Latest Posts
-
Definition Of Prim And Proper
Sep 20, 2025
-
Put Fractions In Order Worksheet
Sep 20, 2025
-
155cm To Inches And Feet
Sep 20, 2025
-
Nice Word Starting With E
Sep 20, 2025
-
Who And When Discovered Hydrogen
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 9 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.