Lcm Of 3 7 5
candidatos
Sep 20, 2025 · 6 min read
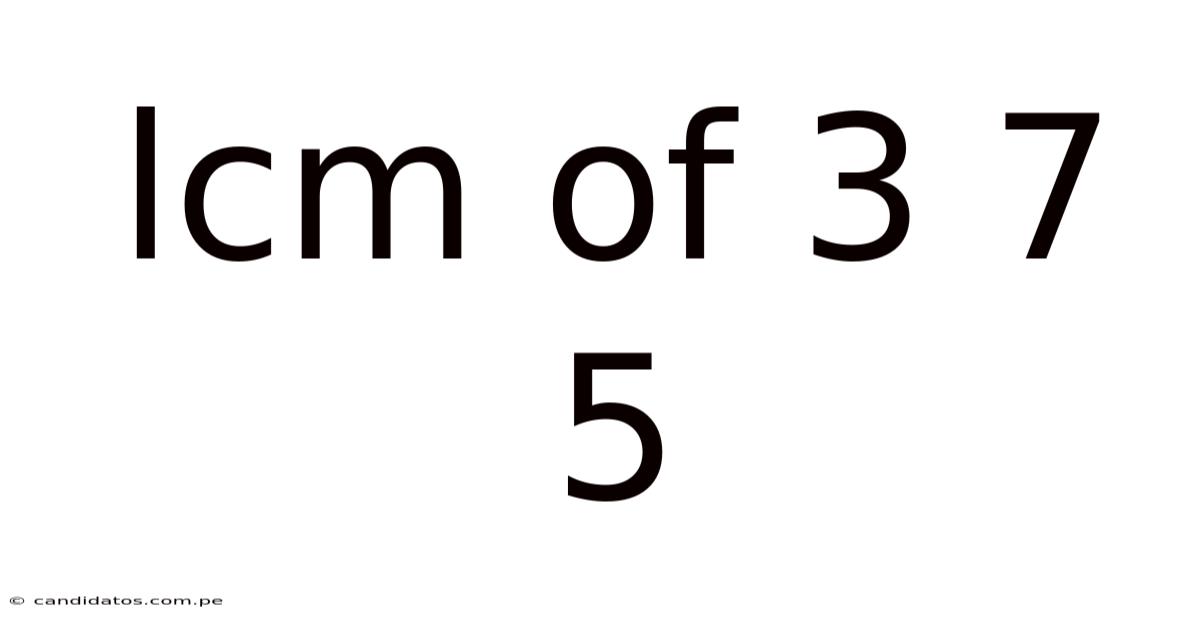
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 7, and 5: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it can be incredibly beneficial, particularly when dealing with larger numbers or more complex scenarios. This comprehensive guide will delve into the process of determining the LCM of 3, 7, and 5, while also exploring the broader implications and applications of LCM in mathematics and beyond. We'll examine various methods, explaining them clearly and thoroughly, making this a valuable resource for students and anyone looking to strengthen their understanding of this fundamental mathematical concept.
Understanding Least Common Multiples (LCM)
Before jumping into the calculation, let's clarify what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the given numbers as factors. This concept is crucial in various mathematical operations and real-world applications, from scheduling events to solving problems in measurement and fractions.
Key Terms:
- Multiple: A multiple of a number is the product of that number and any integer (e.g., multiples of 3 are 3, 6, 9, 12, etc.).
- Common Multiple: A common multiple of two or more numbers is a number that is a multiple of all of them.
- Least Common Multiple (LCM): The smallest positive common multiple of two or more numbers.
Method 1: Listing Multiples
This is the most straightforward method, particularly useful when dealing with smaller numbers like 3, 7, and 5. We simply list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 35, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 70, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105,...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105,...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105,...
By examining the lists, we can see that the smallest number appearing in all three lists is 105. Therefore, the LCM of 3, 7, and 5 is 105.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors involved.
-
Find the prime factorization of each number:
- 3 = 3¹ (3 is a prime number)
- 7 = 7¹ (7 is a prime number)
- 5 = 5¹ (5 is a prime number)
-
Identify the unique prime factors: In this case, we have 3, 7, and 5.
-
Find the highest power of each unique prime factor: Each prime factor appears only to the first power (exponent of 1).
-
Multiply the highest powers together: 3¹ x 7¹ x 5¹ = 105
Therefore, the LCM of 3, 7, and 5 using prime factorization is 105. This method is particularly useful when dealing with larger numbers or sets of more than three numbers because it avoids the lengthy process of listing multiples.
Method 3: Using the Formula (for Two Numbers)
While this method is primarily designed for finding the LCM of two numbers, it can be extended to multiple numbers by finding the LCM iteratively. The formula is:
LCM(a, b) = (a * b) / GCD(a, b)
where GCD(a, b) is the greatest common divisor of a and b.
Let's first find the LCM of 3 and 7:
- Find the GCD of 3 and 7: The greatest common divisor of 3 and 7 is 1 (since they are both prime and have no common factors other than 1).
- Apply the formula: LCM(3, 7) = (3 * 7) / 1 = 21
Now, let's find the LCM of 21 and 5:
- Find the GCD of 21 and 5: The greatest common divisor of 21 and 5 is 1.
- Apply the formula: LCM(21, 5) = (21 * 5) / 1 = 105
Therefore, the LCM of 3, 7, and 5 using this iterative approach is 105. This method demonstrates the relationship between LCM and GCD, showcasing their interconnectedness in number theory.
Real-World Applications of LCM
The concept of LCM extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Scheduling: Imagine you have three different events – one that repeats every 3 days, another every 7 days, and a third every 5 days. Finding the LCM (105) tells you when all three events will coincide again.
-
Fractions: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators. For example, adding 1/3 + 1/7 + 1/5 requires finding the LCM of 3, 7, and 5 (which is 105) to create equivalent fractions with a common denominator.
-
Cyclic Processes: Many natural and engineered systems exhibit cyclical behavior. LCM helps determine when these cycles will align or repeat simultaneously. This is useful in fields like engineering, physics, and even biology.
-
Gear Ratios: In mechanical engineering, LCM plays a role in determining gear ratios to achieve desired speeds and torques.
-
Project Management: In project scheduling, LCM can help determine the optimal time intervals for different tasks to ensure efficient workflow and minimize conflicts.
Frequently Asked Questions (FAQ)
Q: Is there only one LCM for a set of numbers?
A: Yes, there is only one least common multiple for a given set of numbers. There are infinitely many common multiples, but only one is the smallest.
Q: What if the numbers have common factors?
A: The prime factorization method efficiently handles numbers with common factors. The highest power of each unique prime factor is considered, ensuring the LCM is the smallest possible.
Q: Can I use a calculator to find the LCM?
A: Yes, most scientific calculators and online calculators have built-in functions to compute the LCM of a set of numbers.
Q: What if one of the numbers is zero?
A: The LCM of any set of numbers that includes zero is undefined. The concept of LCM only applies to non-zero integers.
Conclusion
Finding the least common multiple of 3, 7, and 5, whether using the listing method, prime factorization, or the iterative GCD approach, consistently yields the answer 105. This seemingly simple calculation highlights a fundamental concept with far-reaching applications in various areas of mathematics and beyond. Understanding LCM isn't just about solving arithmetic problems; it's about grasping the underlying principles of number theory and applying this knowledge to practical situations. The methods described here provide different avenues to arrive at the solution, allowing you to choose the method best suited to the given numbers and your level of understanding. Mastering LCM is a valuable skill that enhances mathematical proficiency and opens doors to solving more complex problems.
Latest Posts
Latest Posts
-
Cooking Is The Blank Giving
Sep 20, 2025
-
Mental Maths Answers Book F
Sep 20, 2025
-
Words Ending In T E
Sep 20, 2025
-
What Is A Promissory Agreement
Sep 20, 2025
-
Shape And Volume Of Gas
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 7 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.