Is 2/3 Larger Than 3/4
candidatos
Sep 18, 2025 · 6 min read
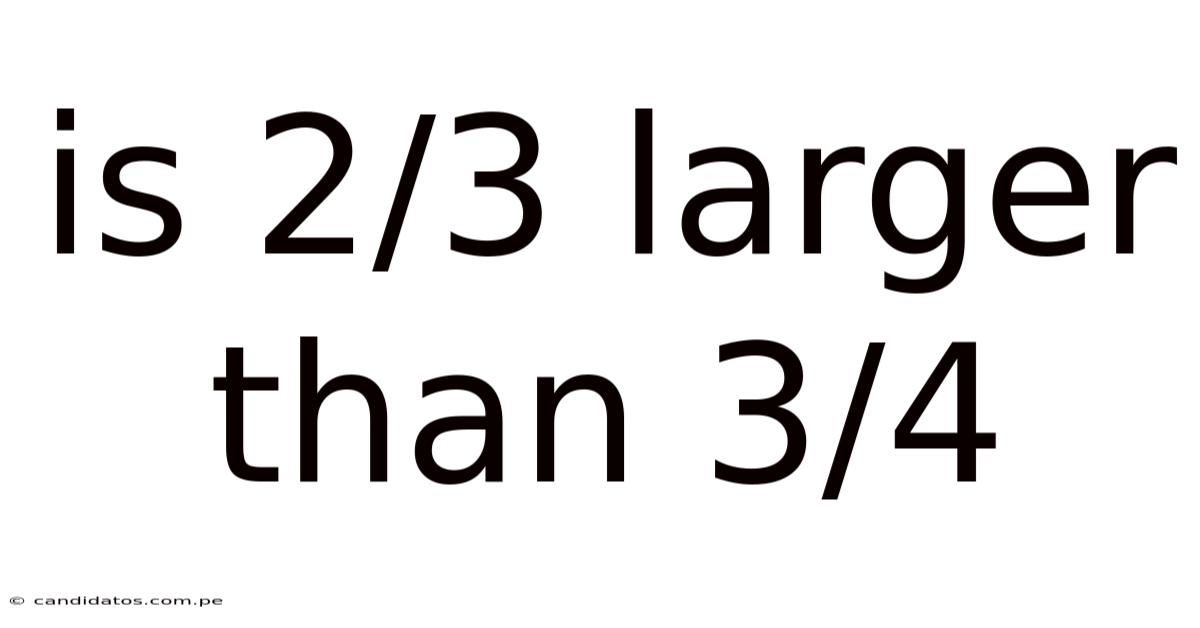
Table of Contents
Is 2/3 Larger Than 3/4? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for various aspects of life, from cooking and construction to finance and scientific research. A common question that arises, especially for students learning about fractions, is whether 2/3 is larger than 3/4. This article will not only answer this question definitively but also explore various methods for comparing fractions, ensuring a comprehensive understanding of this essential mathematical concept. We'll delve into the reasoning behind the comparison, provide practical examples, and address frequently asked questions.
Introduction: Understanding Fractions
Before we tackle the main question, let's briefly review what fractions represent. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering. For instance, in the fraction 2/3, the whole is divided into 3 equal parts, and we're considering 2 of those parts.
Method 1: Finding a Common Denominator
One of the most common and reliable methods for comparing fractions is to find a common denominator. This means finding a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's apply this method to compare 2/3 and 3/4.
-
Find the Least Common Multiple (LCM): The denominators are 3 and 4. The multiples of 3 are 3, 6, 9, 12, 15... and the multiples of 4 are 4, 8, 12, 16... The least common multiple of 3 and 4 is 12.
-
Convert the fractions: We need to convert both fractions to have a denominator of 12.
-
To convert 2/3 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
To convert 3/4 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 3: (3 x 3) / (4 x 3) = 9/12
-
-
Compare the numerators: Now we compare 8/12 and 9/12. Since 8 < 9, we conclude that 8/12 < 9/12.
-
Conclusion: Therefore, 2/3 is smaller than 3/4.
Method 2: Converting to Decimals
Another effective way to compare fractions is by converting them into decimals. This involves dividing the numerator by the denominator.
-
Convert 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667
-
Convert 3/4 to a decimal: 3 ÷ 4 = 0.75
-
Compare the decimals: Since 0.6667 < 0.75, we conclude that 2/3 is smaller than 3/4.
This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator or when you have a calculator readily available. However, remember that decimal representations can sometimes be approximations, especially with repeating decimals like 2/3.
Method 3: Visual Representation
A visual approach can be incredibly helpful, especially for beginners. Imagine two identical pizzas.
-
Pizza 1 (representing 2/3): Cut the pizza into three equal slices. Take two of those slices.
-
Pizza 2 (representing 3/4): Cut the pizza into four equal slices. Take three of those slices.
By visually comparing the amount of pizza you have in each case, it's evident that the three slices from the second pizza (3/4) represent a larger portion than the two slices from the first pizza (2/3).
Method 4: Cross-Multiplication
This method provides a quick way to compare two fractions without finding a common denominator. It involves multiplying the numerator of the first fraction by the denominator of the second fraction, and vice versa. Then, compare the resulting products.
-
Cross-multiply:
-
2 (numerator of 2/3) x 4 (denominator of 3/4) = 8
-
3 (numerator of 3/4) x 3 (denominator of 2/3) = 9
-
-
Compare the products: Since 8 < 9, we conclude that 2/3 is smaller than 3/4.
This method is algebraically equivalent to finding a common denominator, but it often feels more streamlined.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is not just an abstract mathematical skill; it's a practical tool used in numerous real-world scenarios. Imagine you're comparing the prices of two items, each expressed as a fraction of the original price. Or perhaps you're measuring ingredients for a recipe, needing to determine which amount is larger. Mastering fraction comparison ensures accuracy and efficiency in such situations.
Expanding on Fraction Concepts: Further Exploration
While the comparison of 2/3 and 3/4 is a straightforward example, the principles involved extend to more complex fractions. The methods discussed—finding a common denominator, converting to decimals, visual representation, and cross-multiplication—are all applicable to a broader range of fraction comparisons. Understanding these methods forms a strong foundation for tackling more challenging fraction problems, including those involving mixed numbers, improper fractions, and operations with fractions.
Frequently Asked Questions (FAQ)
Q1: Are there any other methods for comparing fractions?
A1: Yes, although less commonly used, you can also compare fractions by converting them to percentages. For example, 2/3 is approximately 66.67%, while 3/4 is 75%. This method is useful when dealing with percentages in real-world applications.
Q2: What if the fractions have very large numbers?
A2: For fractions with very large numbers, using a calculator to convert them to decimals or employing a computer program to find the least common multiple becomes more efficient. Cross-multiplication remains a viable method, though the numbers involved may require careful calculation.
Q3: How can I improve my understanding of fractions?
A3: Practice is key. Work through various examples, starting with simple fractions and gradually increasing the complexity. Use different comparison methods to reinforce your understanding. Visual representations, such as using fraction circles or drawing diagrams, can also be helpful. Utilize online resources, educational videos, and practice exercises to solidify your skills.
Q4: What are some real-world applications of comparing fractions?
A4: Comparing fractions is essential in many fields. In cooking, it’s crucial for precise measurements. In finance, comparing fractions of shares or interest rates is necessary. In construction, accurate measurements involving fractions are vital for precision. Science experiments frequently involve precise measurements and calculations using fractions. Even in everyday life, comparing fractions may be involved when sharing resources fairly or understanding discounts.
Conclusion: Mastering Fraction Comparison
The answer to the initial question, "Is 2/3 larger than 3/4?", is definitively no. 2/3 is smaller than 3/4. This article has explored multiple methods for comparing fractions, highlighting their respective strengths and providing a deeper understanding of this fundamental mathematical concept. By mastering these methods and practicing regularly, you'll not only be able to confidently compare fractions but also build a solid foundation for more advanced mathematical concepts. Remember, a strong grasp of fractions is a cornerstone of mathematical proficiency and has wide-ranging applications in various aspects of life.
Latest Posts
Latest Posts
-
Scientific Name For A Bird
Sep 18, 2025
-
Hsc Advanced Maths Formula Sheet
Sep 18, 2025
-
100 Sq Ft In Feet
Sep 18, 2025
-
Positive Words Beginning With F
Sep 18, 2025
-
Terminating Decimal And Repeating Decimal
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Larger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.