Integral Of 2x 1 2
candidatos
Sep 22, 2025 · 6 min read
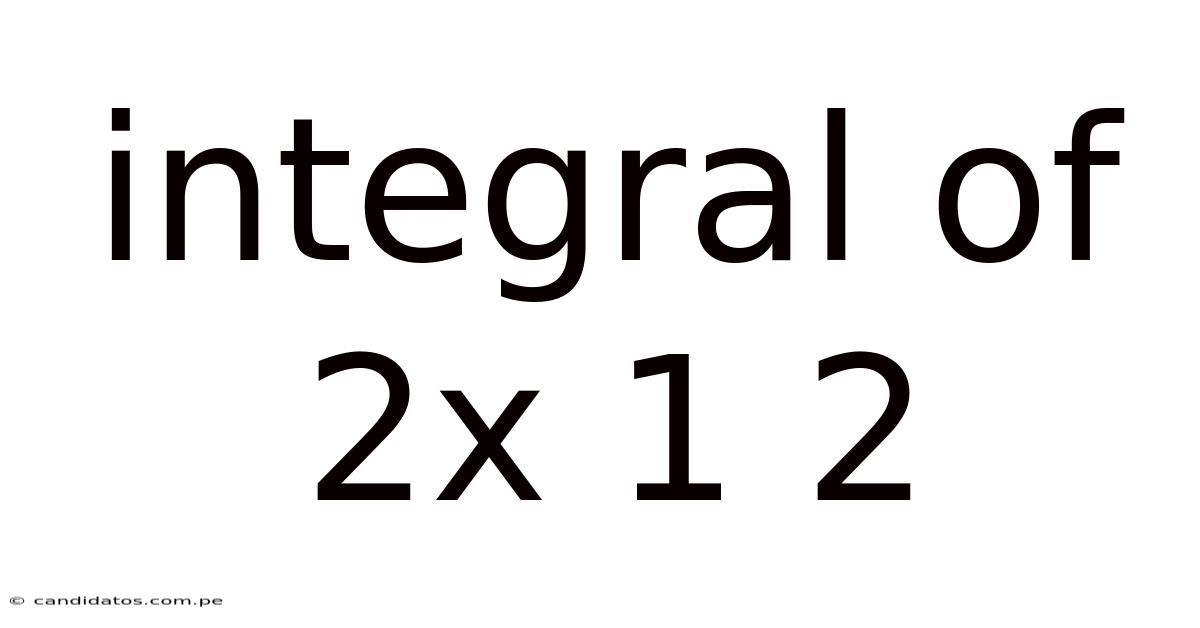
Table of Contents
Decoding the Integral: A Comprehensive Guide to ∫(2x + 1)² dx
The seemingly simple expression ∫(2x + 1)² dx might appear daunting to those unfamiliar with integral calculus. However, with a systematic approach and a solid understanding of basic integration techniques, solving this integral becomes a straightforward process. This article will guide you through the steps, explaining the underlying principles and offering insights to help you tackle similar problems with confidence. We'll explore various methods, delve into the underlying theory, and address common questions, ensuring a comprehensive understanding of this fundamental concept in calculus.
Introduction: Understanding Integration
Before diving into the specifics of integrating (2x + 1)², let's briefly recap the core concept of integration. Integration is essentially the reverse process of differentiation. While differentiation finds the instantaneous rate of change of a function, integration finds the area under the curve of a function. It's a powerful tool used extensively in various fields like physics, engineering, and economics to model and solve real-world problems. The notation ∫ represents the integral sign, f(x) represents the function being integrated (the integrand), and dx indicates that the integration is performed with respect to the variable x. The result of the integration is called the antiderivative or indefinite integral.
Method 1: Expanding and Integrating Term by Term
The most straightforward approach to solving ∫(2x + 1)² dx is to first expand the integrand and then integrate each term separately. This method leverages the linearity property of integrals, which states that the integral of a sum is the sum of the integrals.
Step 1: Expand the Integrand
First, we expand the square:
(2x + 1)² = (2x + 1)(2x + 1) = 4x² + 4x + 1
Step 2: Integrate Term by Term
Now, we can rewrite the integral as:
∫(4x² + 4x + 1) dx
The linearity property allows us to split this into three separate integrals:
∫4x² dx + ∫4x dx + ∫1 dx
Step 3: Apply the Power Rule of Integration
The power rule of integration states that ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, where n ≠ -1 and C is the constant of integration. Applying this rule to each term:
∫4x² dx = 4 * (x³/3) + C₁ = (4/3)x³ + C₁
∫4x dx = 4 * (x²/2) + C₂ = 2x² + C₂
∫1 dx = x + C₃
Step 4: Combine the Results
Combining the results from Step 3 and simplifying, we get:
(4/3)x³ + 2x² + x + C
where C = C₁ + C₂ + C₃ is the overall constant of integration. It's crucial to remember the constant of integration (C) because the derivative of a constant is zero. Therefore, infinitely many functions have the same derivative.
Therefore, the indefinite integral of (2x + 1)² is (4/3)x³ + 2x² + x + C.
Method 2: Using the Substitution Method (u-substitution)
While the expansion method is efficient here, the substitution method offers a powerful alternative, especially for more complex integrals. Let's see how it applies to this problem.
Step 1: Choose a Substitution
Let u = 2x + 1. This simplifies the integrand considerably.
Step 2: Find du/dx
Differentiating u with respect to x, we get:
du/dx = 2
Step 3: Solve for dx
Rearrange the equation to solve for dx:
dx = du/2
Step 4: Substitute and Integrate
Substitute u and dx into the original integral:
∫(2x + 1)² dx = ∫u² (du/2) = (1/2)∫u² du
Now, applying the power rule:
(1/2)∫u² du = (1/2) * (u³/3) + C = (1/6)u³ + C
Step 5: Substitute Back
Finally, substitute back u = 2x + 1:
(1/6)(2x + 1)³ + C
While this result looks different from the previous one, it's algebraically equivalent. Expanding (1/6)(2x + 1)³ will yield (4/3)x³ + 2x² + x + 1/6 + C, where the 1/6 is absorbed into the constant of integration.
The Constant of Integration: A Crucial Detail
The constant of integration, C, is a critical part of the indefinite integral. It represents the family of functions that all have the same derivative. Without C, the solution is incomplete. The value of C is determined only if we have additional information, such as a specific point the function must pass through (a boundary condition).
Definite Integrals: Calculating Area
While we've focused on indefinite integrals (finding the general antiderivative), integration also allows us to calculate the definite integral, which represents the area under the curve between two specified limits (a and b):
∫[a,b] f(x) dx
To calculate a definite integral, we first find the indefinite integral and then evaluate it at the upper and lower limits, subtracting the result at the lower limit from the result at the upper limit. For instance, to find the area under the curve of (2x + 1)² from x = 0 to x = 1, we would do the following:
[(4/3)(1)³ + 2(1)² + 1 + C] - [(4/3)(0)³ + 2(0)² + 0 + C] = (4/3) + 2 + 1 = 13/3
Notice that the constant of integration (C) cancels out when calculating definite integrals.
Applications of Integration
The integral of (2x + 1)² and integration techniques in general are essential for a wide range of applications:
- Physics: Calculating work done by a variable force, finding displacement from velocity, and determining the center of mass of an object.
- Engineering: Designing structures, analyzing fluid flow, and modeling heat transfer.
- Economics: Calculating consumer surplus, producer surplus, and present value of future income streams.
- Probability and Statistics: Finding probabilities using probability density functions.
Frequently Asked Questions (FAQ)
Q1: Why is the constant of integration important?
A1: The constant of integration accounts for the fact that many functions can have the same derivative. It's a consequence of the derivative of a constant being zero.
Q2: Can I use other methods to solve this integral?
A2: Yes, while expansion and substitution are common, you could also use integration by parts (though it's unnecessary here) or numerical integration methods for more complex integrals that lack analytical solutions.
Q3: What if the exponent was different, say (2x + 1)³?
A3: The same principles apply. You could expand the expression (using the binomial theorem for higher powers) or use u-substitution. The calculations will be more involved but the process remains consistent.
Q4: How do I check if my answer is correct?
A4: Differentiate your result. If you get back the original integrand, your integration is correct.
Conclusion: Mastering Integration Techniques
The seemingly simple integral ∫(2x + 1)² dx provides a valuable introduction to fundamental integration techniques. By mastering the methods discussed—expansion and substitution—you'll be well-equipped to tackle a broad range of integration problems. Remember to always include the constant of integration and, when appropriate, use the correct method to evaluate definite integrals to find areas under curves. The ability to integrate effectively is a cornerstone of advanced mathematical understanding and application across numerous scientific and engineering disciplines. With practice and a clear understanding of the underlying principles, you'll be able to confidently solve more complex problems and unlock the power of integral calculus.
Latest Posts
Latest Posts
-
Limitations Of Bronsted Lowry Theory
Sep 22, 2025
-
General Maths Exam 1 2024
Sep 22, 2025
-
Color Name Start With A
Sep 22, 2025
-
20 Out Of 25 Percentage
Sep 22, 2025
-
Poems For Brothers From Sister
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 2x 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.